自适应抗差Kalman滤波在多天线原始观测值瞬时姿态确定中的应用

甘 雨，隋立芬，刘长建，董 明

信息工程大学地理空间信息学院，河南 郑州450000

1 引 言

GNSS测姿具有成本低、初始化快、误差相对稳定等特点，已成为GNSS应用研究的热点。目前在双天线单瞬时定向方面的研究较为深入，一般通过约束条件辅助单基线求解，再基于基线结果计算姿态，这一领域已有丰富成果［1－4］。在多基线方面，有学者研究了整体解算方法［5－6］，但是需先解基线再解姿态，无法直接利用原始观测值测姿。文献［7］提出在多基线解算过程中固定模糊度，再将模糊度回代求解四元数参数，以充分利用观测信息，但本质上仍属基线解算模型。文献［8］以方向余弦阵为姿态参数，利用原始观测值计算方向余弦和模糊度浮点解，将方向余弦的正交约束引入到模糊度搜索中，利用MCLAMBDA方法（multivariate constrained LAMBDA）进行搜索。由于约束信息的引入，使得模糊度的搜索空间不再为椭球体，整周模糊度的搜索负担远高于一般的LAMBDA方法［9］，且方向余弦阵含9个参数，解算效率偏低，影响实时应用。目前未形成可靠的由载波相位观测解算欧拉角或四元数固定解的理论。

现有测姿方法使用最小二乘进行单历元解算以避免周跳探测问题，历史信息没有得到充分利用。使用自适应选权滤波［10］、自适应抗差滤波［11－12］等方法均能高效地平衡历史信息和当前观测，其中自适应抗差滤波具有抵御粗差干扰的能力，在城区及海上姿态测量等应用中能发挥优势。实际上，只要不使用模糊度历史信息，使用滤波的方式也无须探测周跳，可实现瞬时定姿。

本文推导了基于失准角及乘性误差四元数的载波相位观测模型，分别建立有外部角速度传感器和无外部传感器辅助下姿态参数估计的状态模型；使用自适应抗差滤波估计姿态，借鉴分类自适应因子的思想，对模糊度参数和姿态误差参数分别自适应，通过模糊度自适应因子控制模糊度先验值的信任度，若选择极小的自适应因子，可在滤波框架内免去探测周跳过程；根据Ratio值确定姿态参数的自适应因子。自适应抗差滤波能够充分利用约束信息和历史信息，将其融合在浮点解计算过程中，极大提高模糊度浮点解精度及其协方差的结构，在此基础上使用LAMBDA方法即能快速搜索出固定解。采用实测舰载GNSS 3天线测姿算例证明了本文方法的有效性。

2 基于姿态误差和模糊度参数的载波相位观测模型

设在主天线i和天线j同步观测到卫星p、q，可组站星双差观测方程

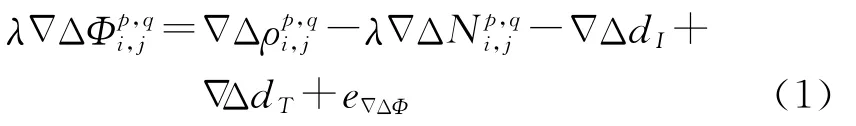
将式（1）在基线初值展开并忽略大气折射延迟项，有

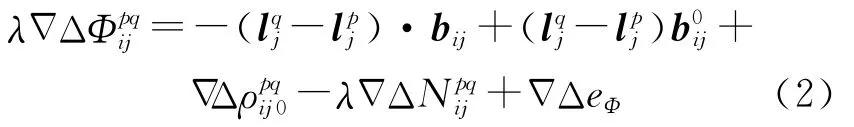
式中，bij为基线参数和为方向余弦矢量；

整理可得基线观测模型为

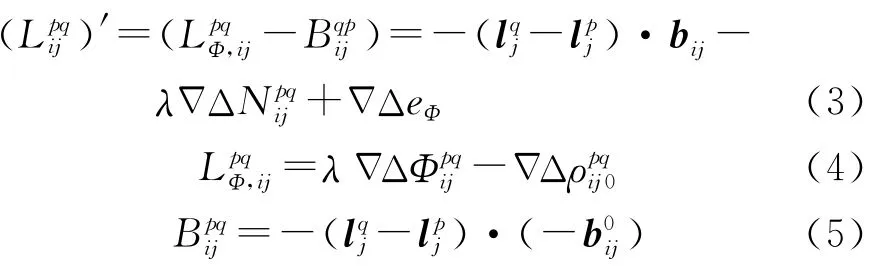
由于GNSS观测方程为非线性，姿态参数之间的关系也为非线性，因此，姿态估计中一般计算名义姿态中包含的姿态误差，再对名义姿态进行误差修正。这里分别从失准角和乘性四元数这两种姿态误差参数的角度推导相应的载波相位观测方程。

设载体坐标系为b系，当地水平坐标系为n系，载体姿态可用姿态矩阵表示。设名义当地水平坐标系为n′系，定义n系到n′系的失准角为φ，它表示实际当地水平系n和名义当地水平系n′之间的旋转矢量，可理解为名义系n′的误差。若失准角较小，其近似等于俯仰、横滚和航向的欧拉角误差，这里为了保证严密性，依旧称之失准角而非欧拉角误差。n和n′之间的关系可用式（6）的姿态矩阵的形式表示［13］

式中，（φ×）为φ的叉乘矩阵，为一反对称阵。

失准角、名义姿态阵、姿态阵之间的关系如式（7）所示

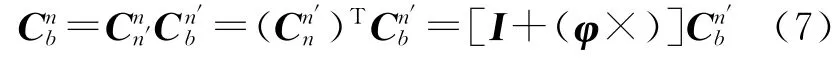
式（3）中的bij为地固系e系中的基线，加上上标为，由坐标旋转关系，有

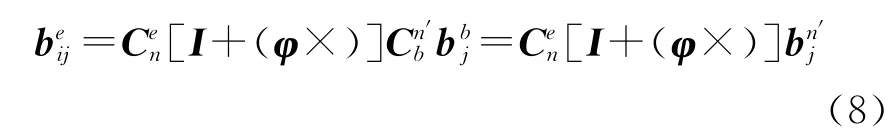
将式（8）代入式（3），得

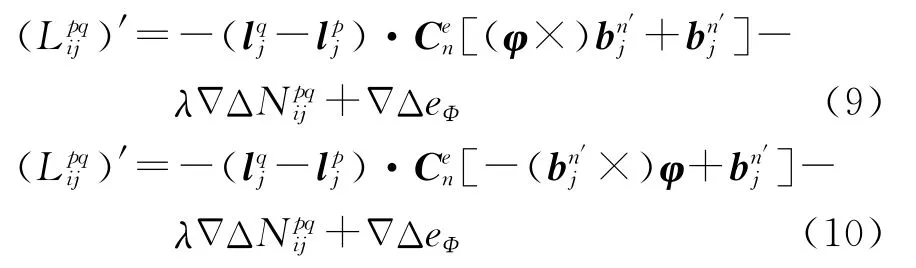
整理可得基于失准角参数的载波相位观测方程

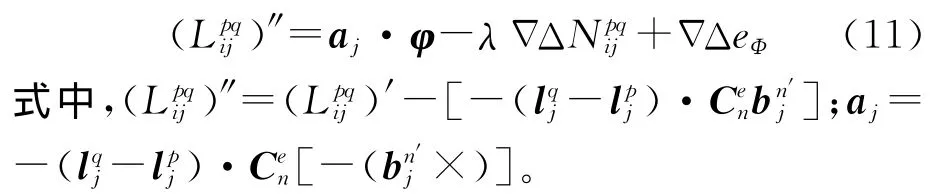
对于天线j1和主天线i，按照式（11）可由所有观测卫星得到矩阵形式的观测方程为

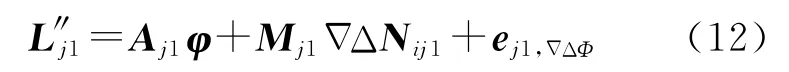
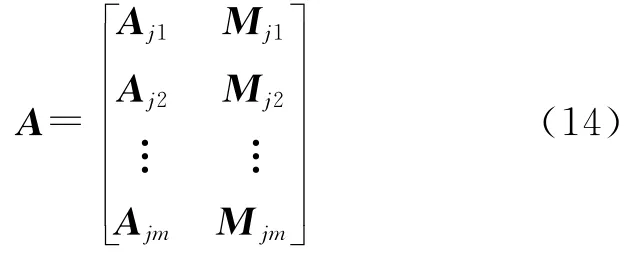
若有天线（j1，j2，…，jm），则基于失准角和模糊度参数（略去双差算子）的载波相位观测模型为

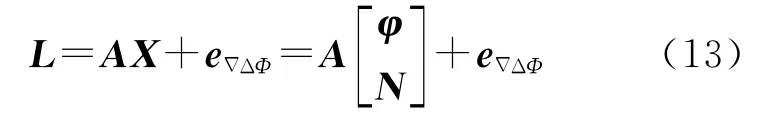
前面推导了基于失准角表示姿态误差的观测方程，也可采用乘性误差四元数的形式。在误差角为小量下，有［13］

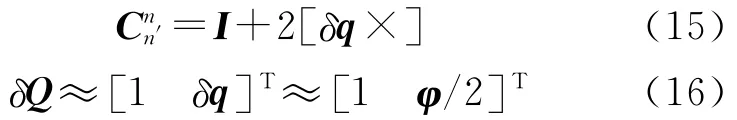
仅需将式（12）稍作改动即可得到基于乘性误差四元数的载波相位观测方程

若GNSS姿态测量系统含m条基线，使用基线解算模型需解算3m个基线参数，而使用基于失准角或误差四元数的观测值模型仅解算3个姿态参数，效率更高。

3 姿态估计的状态模型

四元数微分方程为［7］

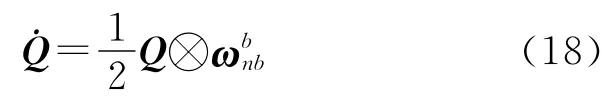
由姿态矩阵与姿态四元数之间的关系可得乘性误差四元数δQ满足

将式（18）、式（19）代入式（21）

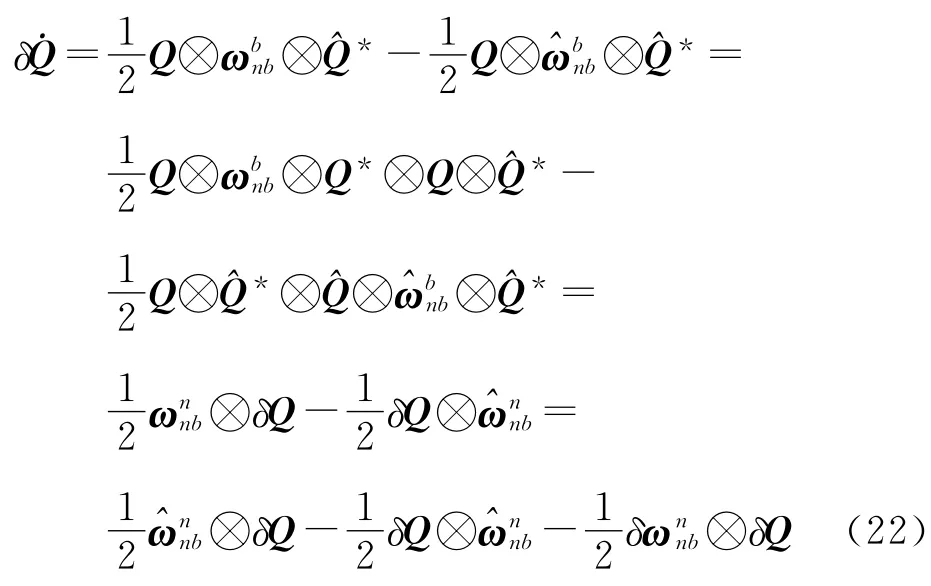
根据四元数乘法准则，得

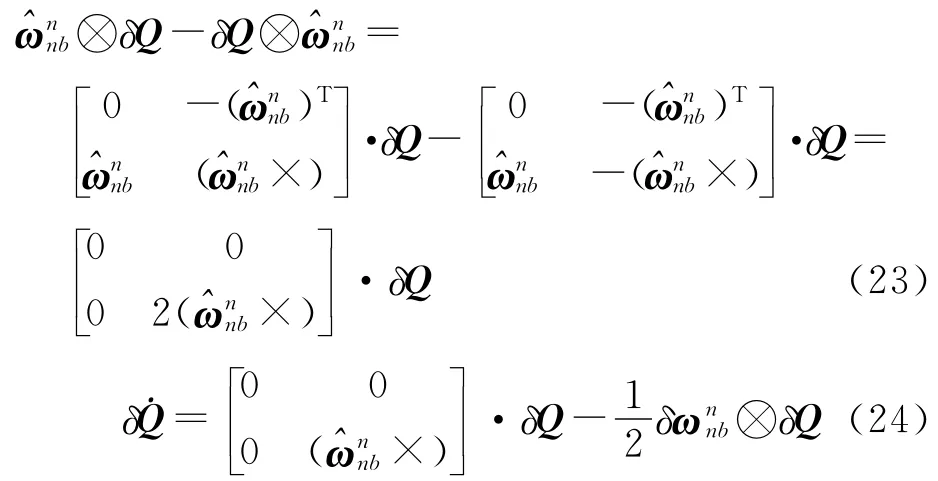
由式（16），得

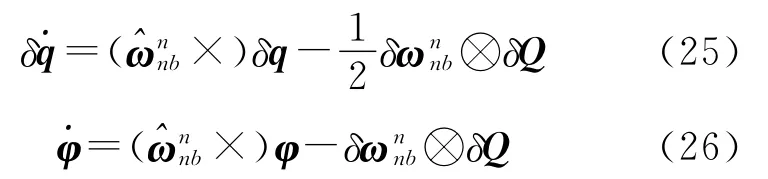
式（25）、式（26）的右端第2项即为状态噪声。

若有外部角速度传感器如陀螺仪的辅助，则可直接使用式（25）或式（26）建立状态方程，否则，无法获得角速度，此时将式（26）改化为

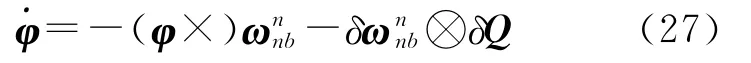
将ω扩展为状态参数并用随机游走模型表示，纳入式（27）并离散化

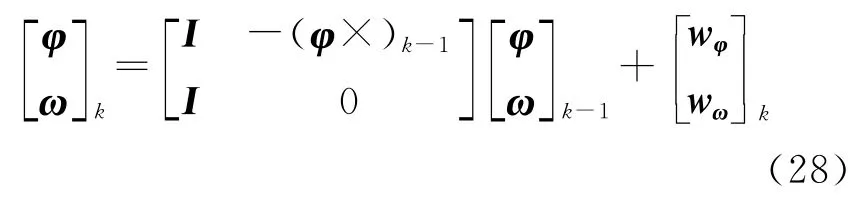
即为无外部角速度传感器辅助下的姿态估计状态模型。

4 自适应抗差滤波的应用及自适应因子的确定

综合式（13）、式（28）可得基于载波相位观测值估计姿态的滤波模型为

式（30）中的A与式（13）略有不同，为

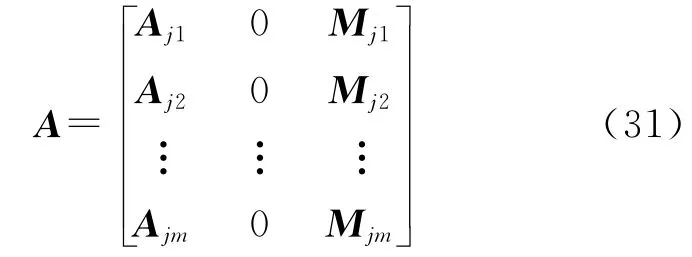
使用姿态误差而非姿态本身作为滤波中的姿态参数，可以减小观测方程线性化引起的模型误差。设计算的名义姿态阵，滤波估计得到的失准角，代入式（6）、式（7），即可对名义姿态进行修正，修正后的即为滤波解。在k时刻，以k－1时刻的滤波解作为名义解。若k时刻成功固定模糊度即得到失准角固定解时，应在完成姿态修正后将失准角置零后传递至下一历元。

若前一时刻姿态估计精度高，则本时刻名义解较为可靠，应信任状态预测信息，若名义解精度不高，则使用自适应因子减小状态信息的贡献。

姿态误差、角速度、模糊度属不同类型的参数，很难采用统一的自适应因子进行调节，分类因子自适应滤波可对不同的分量选取不同的自适应因子。分类因子自适应抗差滤波解为［14－15］

式中，为抗差等价权矩阵，可由Huber函数确定［15］

式中，为标准化残差；c为常量，可取1.0～1.5。

为状态预测的自适应权矩阵，有

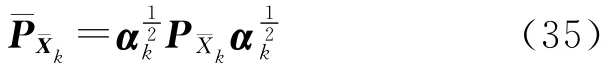
式中，αk为自适应因子矩阵，即

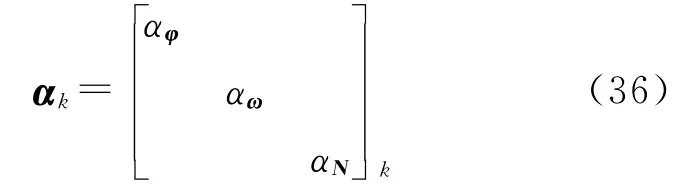
由于ω为间接观测量，这里不作自适应，有

αN可调整模糊度先验信息的权重，若进行周跳探测得到各卫星中最大周跳估值为dN，顾及周跳探测量自身的噪声，可选取自适应因子为

式中，σ¯N为模糊度预测标准差，主要由设定的模糊度状态噪声决定；σDT为周跳探测量的中误差，周跳估值越大，模糊度自适应因子越小，一般αN＜1。

若要免去周跳探测步骤以便瞬时解算，则可取αN为一极小值，如αN＝1.0e－8，此时，模糊度先验信息的权重降至极小，不受周跳干扰。

自适应滤波常用的误差判别统计量包括状态不符值或预测残差等，GNSS定姿中，在模糊度固定前，无法获得足够精度的上述统计量。考虑姿态误差的预测性能本质上由名义解即前一历元姿态滤波解的精度决定，其对应的Ratio值能够在一定程度上反映其可靠程度，αφ由三段函数表示

式中，Rat为Ratio值，一般取c0＝2、c1＝3。

5 计算与比较

本文算例使用实测舰载GPS 3个天线姿态测量双频数据进行计算和比较分析，3个天线构成两条独立基线，基线的载体系坐标分别为［0.0 15.0 0.0］T、［14.5 25.1 0.0］T。由于海面环境复杂，加之天线间距离较远，双差后部分观测值仍受到较为严重的多路径效应影响，以单个历元而言它们表现出粗差性质。姿态解算中模糊度固定解的搜索均采用LAMBDA方法，若Ratio值超过3，则视相应历元成功固定。设计以下4种方案计算浮点解进行对比。

方案1：单历元最小二乘；

方案2：单历元抗差估计；

方案3：自适应滤波；

方案4：自适应抗差滤波。

方案3和方案4中，取模糊度自适应因子αN＝1.0e－8，即完全不使用模糊度先验信息，以和方案1、方案2形成对照，因此4个方案均无须主探测周跳。方案3中仅使用了自适应因子，未使用抗差等价权控制粗差干扰。共有1800个观测历元，表1所示为各方案的模糊度固定结果比较，图1为观测卫星数及PDOP值，图2—图5分别为各方案的航向角估计结果，其中固定解用直线绘制，浮点解用“＊”表示。图6—图9分别为各方案的模糊度精度衰减因子ADOP值结果。ADOP能有效表征模型几何强度，可对模糊度固定成功率进行近似［16］。虽没有外部姿态结果作为参考真值，但只要模糊度固定正确，4种方案的姿态结果基本一致，而姿态浮点解相对固定解会有较大突变，这点可由图1—图4看出，因此，主要从模糊度固定成功率的角度评价4种方案。采用“逐历元L＋MCLABMDA”的方法也进行了解算，但MCLAMBDA算法无法使用Ratio检验等方法评价固定效果，对比他们的模糊度固定解，MCLAMBDA算法中1783个历元的解与本文自适应抗差滤波法完全相同，说明两种方法的正确率相当，这里主要比较它与本文方法的效率差异，结果如表2所示（计算平台：HP dv4－3124tx）。

表1 模糊度固定结果Tab.1 Results of Ambiguity Fixing

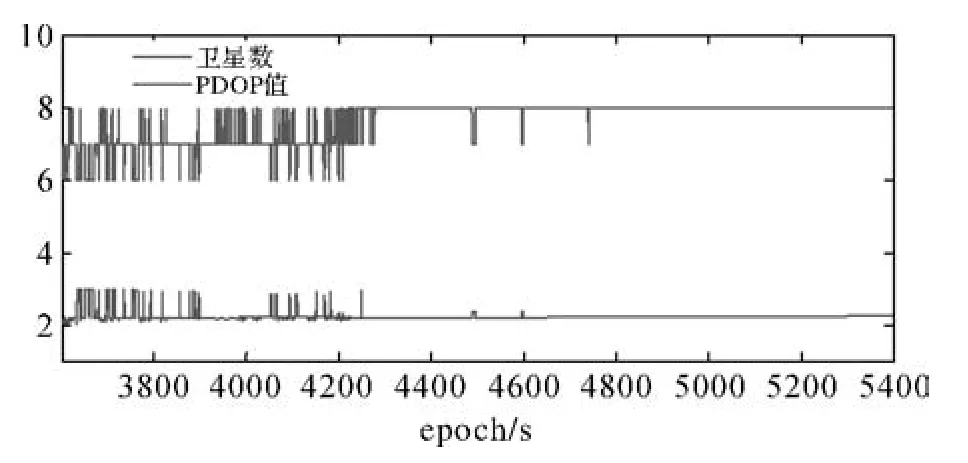
图1 观测卫星数及PDOP值Fig.1 Observed satellite number and PDOP

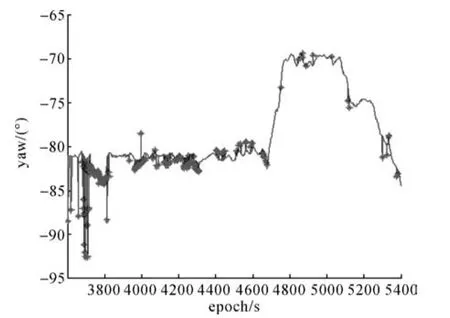
图2 方案1航向角Fig.2 Yaw of scheme 1

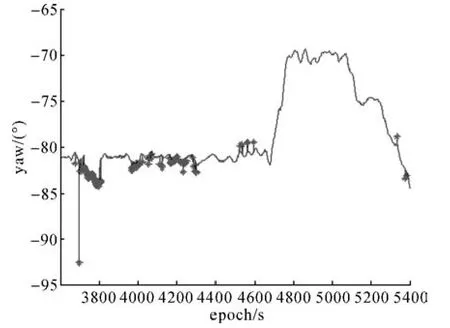
图3 方案2航向角Fig.3 Yaw of scheme 2

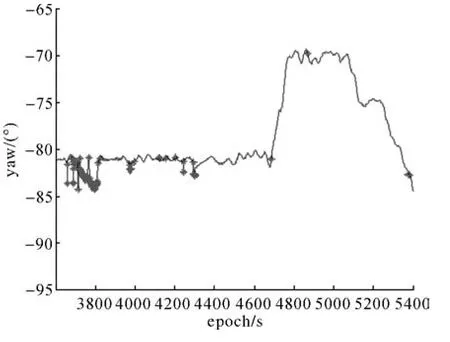
图4 方案3航向角Fig.4 Yaw of scheme 3

表2 所有历元姿态解算总耗时Tab.2 Total time cost of attitude determination of all epochs s

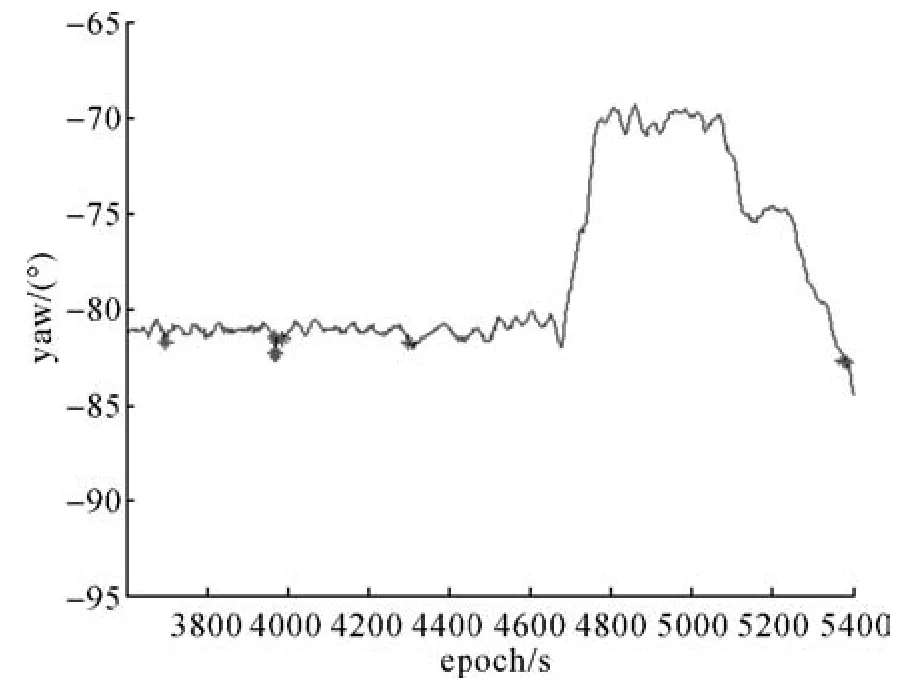
图5 方案4航向角Fig.5 Yaw of scheme 4

图6 方案1的ADOP值Fig.6 ADOP of scheme 1

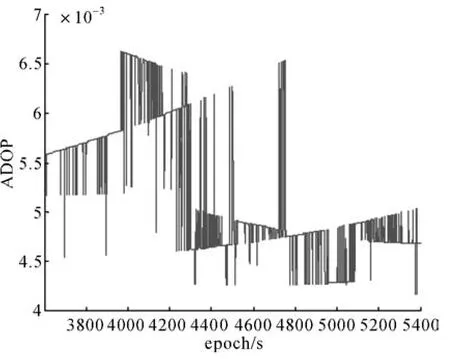
图7 方案2的ADOP值Fig.7 ADOP of scheme 2

从以上结果可以看出：

（1）相对于最小二乘，抗差估计能够较好地抵制粗差干扰，提高测姿的可靠性，但是由于未充分利用历史信息，仅由当前观测值定姿的成功率不高。抗差估计结果的ADOP结果较最小二乘略差，因为抗差估计对粗差观测值进行降权，观测值整体利用率更低。

图8 方案3的ADOP值Fig.8 ADOP of scheme 3

图9 方案4的ADOP值Fig.9 ADOP of scheme 4

（2）自适应滤波通过自适应因子合理利用历史约束信息，改善观测结构，提高固定率，并具备一定的抗粗差能力，但整体上仍受到粗差观测值影响。

（3）自适应抗差滤波能够合理利用姿态历史信息，改善整体的结构，显著减小ADOP值，且很好地抵御了粗差干扰，大大提高模糊度固定成功率。实际上9个未成功固定的历元中，有4个历元固定解正确而未通过Ratio检验，而在另外5个历元处存在较多粗差，同时自适应因子为0，观测结构较差，无法得到可靠的浮点解。

（4）由于在搜索过程中引入约束条件，MCLAMBDA的计算效率较低，耗时远高于自适应抗差滤波方法。通常自适应抗差滤波比最小二乘更为耗时（如浮点解计算阶段），但由于自适应抗差滤波得到的浮点解精度高于最小二乘，因此在模糊度搜索过程中更快，整体上效率稍高。

6 结 论

目前没有可靠的由GNSS载波相位观测值直接解算欧拉角或四元数的理论。基于原始观测值直接定姿的难点在于如何合理利用约束信息，自适应抗差Kalman滤波能将姿态约束信息通过状态模型与当前的观测模型融合起来，本文通过建立合适的状态模型和调节自适应因子，最大限度地发挥历史信息的作用，同时通过抗差等价权抵制粗差观测值的影响，实现可靠、高效的姿态确定。除自适应因子减小同时又出现粗差这类情况，本文方法均能实现瞬时姿态解算。通过模糊度参数的自适应，可以结合周跳探测结果调整模糊度历史信息的权重，并可转换为无须周跳探测的模式，增加了数据处理的灵活性。

本文建立姿态估计状态模型可以用于陀螺等外部传感器和GNSS进行组合测姿的情况，因此自适应抗差Kalman滤波实现瞬时姿态确定的方法能用于任何含多天线GNSS的姿态测量系统中，具有广阔的应用前景。

［1］LIU Zhijian，LIU Yi.Algorithm of a Real－time Attitude System Using Non－dedicated GPS Receivers［J］.Acta Geodaetica et Cartographica Sinica，2005，34（3）：213－217.（刘志俭，刘毅.一种基于非专用接收机的GPS实时定姿算法［J］.测绘学报，2005，34（3）：213－217.）

［2］LIU Genyou，OU Jikun.Determining Attitude with Single Epoch GPS Algorithm and Its Precision Analysis［J］.Geomatics and Information Science of Wuhan University，2003，28（6）：732－735.（刘根友，欧吉坤.GPS单历元定向和测姿算法及其精度分析［J］.武汉大学学报：信息科学版，2003，28（6）：732－735.）

［3］LI Zhenghang，LIU Wanke，LOU Yidong，et al.Heading Determination Algorithm with Single Epoch Dual－frequency GPS Data［J］.Geomatics and Information Science of Wuhan University，2007，32（9）：753－756.（李征航，刘万科，楼益栋，等.基于双频GPS数据的单历元定向算法研究［J］.武汉大学学报：信息科学版，2007，32（9）：753－756.）

［4］TANG Weiming，LI Di，CHI Fengming.Research on Single Epoch Orientation Algorithm of BeiDou Navigation Satellite System［J］.Geomatics and Information Science of Wuhan University，2013，38（9）：1014－1017.（唐卫明，李笛，迟凤明.北斗卫星导航系统单历元定向算法研究［J］.武汉大学学报：信息科学版，2013，38（9）：1014－1017.）

［5］LU Gang，CANNON M E.Attitude Determination Using a Multi－antenna GPS System for Hydrographic Applications［J］.Marine Geodesy，1994，17（4）：237－250.

［6］WANG C，LACHAPELLE G.GPS Attitude Determina－tion Reliability Performance Improvement Using Low Cost Receivers［C］∥Proceedings of the 15th International Technical Meeting of the Satellite Division of the Institute of Navigation.Portland，OR：［s.n.］，2002：1064－1074.

［7］SCHLEPPE J.Development of a Real－time Attitude System Using a Quaternion Parameterization and Non－dedicated GPS Receivers［D］.Alberta，Canada：The University of Calgary，1996.

［8］TEUNISSEN P J G.A General Multivariate Formulation of the Multi－antenna GNSS Attitude Determination Problem［J］.Artificial Satellites，2007，42（2）：97－111.

［9］W ANG Bing，SUI Lifen，ZHANG Qinghua，et al.Research on Attitude Determination Algorithms Using GPS［J］.Geomatics and Information Science of Wuhan University，2013，38（12）：1392－1395.（王冰，隋立芬，张清华，等.利用GPS解算载体测姿的算法研究［J］.武汉大学学报：信息科学版，38（12）：1392－1395.）

［10］CHAI Yanju.Theory and Method for Improving the Navigation Accuracy of GPS/INS Integration by Digging the Hidden Information［D］.Wuhan：Institute of Geodesy and Geophysics，Chinese Academy of Sciences，2008.（柴艳菊.挖掘信息提高GPS/INS导航精度的理论与方法研究［D］.武汉：中国科学院测量与地球物理研究所，2008.）

［11］YANG Yuanxi，HE Haibo，XU Guochang.A New Adaptively Robust Filtering for Kinematic Geodetic Positioning［J］.Journal of Geodesy，2001，75（2－3）：109－116.

［12］YANG Yuanxi，HE Haibo，XU Tianhe.Adaptive Robust Filtering for Kinematic GPS Positioning［J］.Acta Geodaetica et Cartographica Sinica，2001，30（4）：293－298.（杨元喜，何海波，徐天河.论动态自适应滤波［J］.测绘学报，2001，30（4）：293－298.）

［13］MARKLEY F L.Attitude Error Representations for Kalman Filtering［J］.Journal of Guidance，Control，and Dynamics，2003，26（2）：311－317.

［14］CUI Xianqiang，YANG Yuanxi.Adaptively Robust Filterring with Classified Adaptive Factors［J］.Progress in Natural Science，2006，16（4）：490－494.（崔先强，杨元喜.分类因子自适应抗差滤波［J］.自然科学进展，2006，16（4）：490－494.）

［15］YANG Yuanxi，CUI Xianqiang.Adaptively Robust Filter with Multi Adaptive Factors［J］.Survey Review，2008，40（309）：260－270.

［16］ODIJK D，TEUNISSEN PJG.ADOP in Closed Form for a Hierarchy of Multi－frequency Single－baseline GNSS Models［J］.Journal of Geodesy，2008，82（8）：473－492.