让复习课堂更厚重

张红娜 河南省许昌市普通教育教学研究室小学数学教研员，中学高级教师。许昌市专业技术拔尖人才，“巾帼建功”标兵，“三八红旗手”;河南省中小学教师教育专家，学科带头人，推进素质教育“百名名师”之一，优秀教研员;中国教育学会小学数学教学专业委员会先进工作者，课程教材研究所小学数学课程教材研究开发中心优秀教研员。

工作中始终坚持“以研导教、以教促研”的教研宗旨，逐渐形成了“严谨、求实、厚重、灵动”的教研风格。执教的课先后在省、国家级赛课中获得一等奖;主持的课题有三项获得省级科研成果一等奖，一项获国家级“十一五”重点课题成果一等奖，目前正在进行河南省教育科学“十二五”规划重点课题《小学数学厚重课堂的探索与实践》的研究;撰写的文章有10多篇在省级以上评比中获奖，30多篇在省级以上专业学术期刊上发表;辅导的青年教师有20多人次在省级以上教学评比中获得一等奖。先后参与多种教辅资料的编写工作，并多次应邀参加全国学术交流活动，并作课、评课，受到好评。

根据学生的认知特点和认知规律，复习是学习过程中一个不可或缺的重要环节。及时、有效地复习，不仅可以引导和帮助学生对已学知识进行巩固和梳理，而且能及时发现存在的问题并进行查漏和补缺，“学而时习之，不亦说乎”，学生还能在其中获得良好的情感体验。所以，复习是学生学习过程中有价值的“驻足回望”。同时，它也能为学生的后续学习集聚能量，以便更好地“扬帆远航”。

《数学课程标准》（2011年版）强调：“教学应激发学生的兴趣，调动学生的积极性，引发学生的数学思考，鼓励学生的创造性思维;要注重培养学生良好的数学学习习惯，使学生掌握恰当的数学学习方法。”这一要求对复习课的教学尤其具有指导意义。下面就结合有关“图形问题”的复习来谈谈如何运用上述理念，有效开展复习教学。

一、在活动中巩固旧知

本节课有关图形问题的复习容量很大、内涵丰富、目标明确：掌握部分平面图形（长方形、正方形、圆形）和立体图形（长方体、正方体、圆柱体）的特征以及它们之间的联系;掌握周长、面积、体积的计算方法;进一步形成分类和转化的思想方法;感悟比较、概括等数学特有的思维方式。要达成上述教学目标，不能生硬地、用一问一答的方式来完成，而是要将其放在具体的数学活动和解决问题中进行有效梳理与巩固。我设计了三个有结构、有层次、有深度的数学活动：（1）“围一围”。让学生在“围一围”的活动中进一步巩固对所学图形的基本特征的认知，并沟通图形之间的逻辑联系;（2）“比一比”。渗透学法指导，让学生在“比一比”的数学活动中学会数学地思考，学会合理灵活地选择解决问题的策略;（3）“填一填”。让学生在“填一填”的活动中感受探究发现的乐趣、数学知识的魅力，获得良好的数学学习情感体验。

数学活动一：“围一围”。

1.由“线”围成“面”

（1）提出问题。

出示一根铁丝并配放课件，教师提问：

①你能用这根铁丝分别围出我们认识的这几个封闭的平面图形吗？

②长方形、正方形和圆相比，用铁丝围出哪个图形更容易一些？哪个图形不太容易围？为什么？

（2）动手操作。

学生按照直觉猜测的难易顺序，先独立用学具尝试围一围，再在小组内、全班交流操作、思考的活动体会。

2.由“面”围成“体”

（1）提出问题。

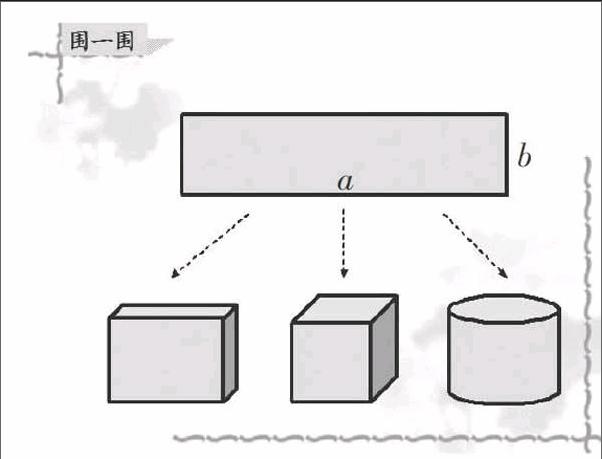
出示一张长方形纸并配放课件（如下），教师提问：

①你能用这样的长方形纸分别围出我们认识的这三种柱体（长方体、正方体、圆柱体）吗？（要求：以长a为底面周长，宽b为高围出三种柱体纸筒）

②猜猜看：最容易围的形体是哪一个，最不易围的又是哪一个呢？

（2）动手操作。

学生带着猜测尝试操作，并在小组内交流体会，教师巡视发现情况，然后全班交流。

①易难顺序：圆柱体—长方体—正方体。

这次活动的焦点出现在围正方体上，学生通过尝试、交流发现：在不改变长方形纸的大小的前提下，不是任意长方形纸都能围成正方体的;只有长是宽的4倍的长方形纸，才能围出正方体。

②再次操作：教师出示三张一样（长是宽的4倍）的长方形纸，指名学生以宽为高，按照由易到难的顺序（引导学生悟出：圆柱体—正方体—长方体）逐一围出三种形体的纸筒，并出示在黑板上。

这样的设计，改变了传统复习中单一的、枯燥的整理基础知识的状况，于具体活动中无痕渗透、自然涉及，效果非常好。

二、在网络中沟通联系

数学知识的内在联系是非常紧密的。通过复习，应该把平时课堂教学中相对零散的知识巧妙地串起来，让学生不仅从中看到知识间的联系，而且感悟到知识在联系中的不断发展。本节课的设计先由线段围出平面图形，再由平面图形围出立体图形。这种线—面—体的教学思路很清晰地为学生提供了一张由一维到二维再到三维的知识网络图，学生从中很容易地感受到图形空间的变化，感受到图形之间的联系和发展。其次，在平面图形围立体图形的环节中，也让学生自悟出长方体、正方体、圆柱体的侧面积都可以用底面周长和高来计算，使算法之间也沟通了联系，达到了统一。

通过“围一围”的学习活动，引导学生再次体悟：掌握形体的特征是正确围出形体的重要前提;从一维的线到二维的面再到三维的体，图形之间有着密切的联系。我及时用课件将两次活动串播如下：

这一网络图凸显了图形结构的连贯性和发展性，它将深深地储存在学生的脑海中，形成良好的三维图形的空间观念。

三、在比较中渗透思想方法

数学思想方法是数学的灵魂，图形问题的复习背后蕴含着重要的思想方法。在复习过程中，我不失时机地进行了相关思想方法的渗透。如：在上述“围一围”的环节中，渗透了联系、转化等思想;在下面“比一比”的活动中，渗透了比较、类推等思想。同时还引导学生认识并使用了例举、推理等重要的数学方法和策略。我想，这对学生的学习是终身受用的。

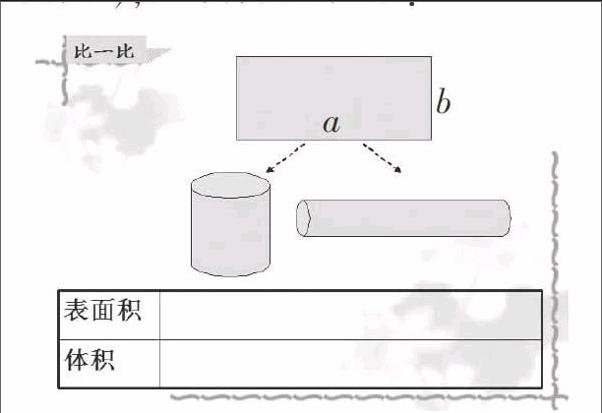
数学活动二：“比一比”。

1.比平面图形

（1）提出问题。

课件出示铁丝围出的三个平面图形，教师提问：这三个图形的周长比怎么样？面积呢？谁的面积最大？谁的面积最小？你是怎么知道的？

（2）尝试比较。

引导学生用举例的方法来比。

生1：用举例子算一算的方法可以知道圆的面积最大，长方形面积最小。

生2：先确定一个长度作为三个图形的周长，然后根据周长和面积的计算方法再求出各自的面积，最后进行比较。

生3：在计算的过程中，圆的面积计算难度较大。

（3）引导小结。

遇到这样的问题，我们可以通过例举法来得出结论（板书：例举）。在例举的过程中，可以有技巧地选择一些数据使计算简便。如：假设π≈3，可以选择2、3、4的公倍数作为它们的周长来计算并比较面积，这样使计算更简便。

2.比立体图形

（1）提出问题。

课件出示长方形围出的三个柱体，教师提问：如果给这三个形体的纸筒都配上底面，你能比较出它们的表面积、体积的大小吗？你是怎么比较出来的？

（2）尝试比较。

①表面积比：S长

生：因为它们的侧面积相等——都是这张长方形纸的面积，只需要比较它们底面积的大小。根据上面比较三个平面图形得出的结论，可以不计算就能推理得出圆柱的表面积最大，长方体的表面积最小。

②体积比：V长

生：因为三个形体等高，所以直接比较底面积就可推理出体积的大小。

教师引导小结：正是有了比较上面三个平面图形面积大小的结论，所以对三个相应的形体体积的比较就不必例举，可以直接推理得出结论。（板书：推理）

通过两次“比”的活动，学生不但强化了相关图形的周长、面积、体积的计算方法，更重要的是知道了例举、推理这些解决问题的策略，使相关数学思想方法的培养落到了实处。

四、在拓展中提升思维

“温故而知新”，“温故”是为了更好地“知新”，学生通过复习巩固知识、积累经验、反省内化，进而生成智慧，方能厚积而薄发。所以，复习不同于新授，通过复习，使学生的数学思维得到一定的提升，这是复习教学的一个目标和方向。

本着复习既是回望过去，更是面向未来的教学追求，本节课我除设计了思维含量一般的活动“用一根铁丝围长方形、用一张普通的长方形纸（长不是宽的4倍）围正方体纸筒”外，还设计了一个思维含量较高的活动（见数学活动三）“比较胖、瘦圆柱体的体积之比与长方形长、宽之比的关系”。通过问题的驱动，让学生的数学思维在矛盾中不断碰撞，在碰撞中不断完善和提升，促使学生逐步养成良好的数学思维习惯，感受数学的神奇和魅力。

数学活动三：“填一填”。

教师不失时机地引导学生用学到的方法继续来比一比、填一填，进一步激发学生探究的欲望，感悟数学探究的乐趣。

1.提出问题

先直观演示：用同一张长方形纸可以围出不同的圆柱形纸筒（以长作底面周长、宽作高围出的“胖圆柱”;以宽作底面周长、长作高围出的“瘦圆柱”），再课件出示如下：

如果给两个纸筒都配上底面，比一比：这两个圆柱的表面积哪个大？体积呢？你是怎么知道的？

教师提示学生，在解决问题时选择相应的策略进行比较。

（1）表面积比：S胖>S瘦（策略：推理）。

（2）体积比：V胖>V瘦（策略：例举）。

2.拓展问题

这两个圆柱体积的比与长方形纸长和宽的比有什么关系？课后请同学们继续思考！

这一问题的提出将本节课的复习延伸到课外，它是“不同的人在数学上得到不同的发展”这一新课程理念的落实，激发了对数学有浓厚兴趣的学生不断探究的强烈欲望，成为学生欣赏、领悟数学美的重要载体。？筻