预测控制算法在硝酸温度控制中的应用研究

刘新梦 林红权,2 曾隽芳,2 马增良

(1.中国科学院自动化研究所,北京 100190；2.北京三博中自科技有限公司，北京 100190)

硝酸广泛应用于航天及化工等领域。工业硝酸生产过程中极为重要的控制环节是氧化炉氨空比与温度的控制，氨空比与氧化炉反应温度直接影响硝酸成品的质量，氨空比是整个硝酸生产过程中的关键。氧化炉作为氨气与空气混合反应的主要设备，其温度是生产过程中极为重要的控制指标，加之温度本身具有滞后性和非线性，采用传统PID控制策略实现氧化炉温度控制存在明显的波动。 为此，以某实际双加压法硝酸生产工艺为背景，在分析氧化炉温度特性的基础上，提出采用模型预测的控制策略，并在建立氨空比与温度模型的基础上仿真分析了模型预测控制算法相比传统控制算法的优势。

硝酸的整个生产工艺流程如图1所示，氨气与空气反应的主要设备为氧化炉。硝酸生产过程中，首先是氨空混合气的制备，氨气与空气混合之后进入氧化炉反应制取NOx气体。NOx气体被送入漂白塔底部进行漂白，经过氧化氮精分离器、二次空气加热器、高压反应水冷凝器后，最终进入吸收塔底部，与工艺水泵送至塔顶的工艺水逆流接触反应生成硝酸。高压反应水冷凝器生成的冷凝酸最终被送入氧化氮分离器[1～3]。

图1 硝酸生产工艺流程示意图

整套硝酸生产过程中，主要有3个关键控制点：氨氧化工艺指标、NOx吸收工艺指标和成品酸的质量。在此仅针对氨氧化工艺部分的控制进行研究。氨氧化工艺指标有：氧化炉温度850～880℃、氨氧化压力350～450kPa和氨空比9.35%～9.75%。

2 氨空比模型的建立

建立模型的基础是获得相应模型的数据。该工艺模型的数据是基于OPC协议通过WinCC与Matlab软件得到的。具体实现方法是利用Matlab的OPC工具箱，WinCC作为OPC Server，Matlab作为OPC Client进行数据的实时采集与交换。氨空比模型参数的求取主要包含模型阶次和模型参数的确定。采用阶跃响应法，在氨空比为9.50%且现场生产较为平稳的情况下加入0.05%的阶跃信号，测取氧化炉温度变化，在此基础上进行建模。

2.1 模型阶次的确定

通过均值E(D)、方差Var(D)、最终预测偏差(FPE)和Best fit共同确定模型的阶次。其中，均值E(D)和方差Var(D)分别为：

(1)

评价所建立的预测模型是否合适或可接受，通常有不同的标准。统计检验是评价模型预测效果的一个比较常用的办法。统计检验的基本原理：首先由模型的使用者根据需要事先指定一个可接受的误差标准数值e和一个小概率α，如果统计检验误差D满足P(|D|≤e)≥1-α，则模型被认为是可以接受的。如果α值很小，意味着模型产生的误差D总体上将以很高的概率小于e，此时认为模型是可以接受的。

通过OPC协议得到现场的实时数据，对其进行建模，得到各个不同阶次模型的输出温度与实际氧化炉温度(表1)。

表1 实际温度与不同阶次下的 模型输出温度 ℃

从Best fit指标来看，一阶模型的控制效果不是很理想，其他3个阶次模型的效果大致一样。依据FPE准则——节省原理(Principle of Parsimony)，即在提供的信息量基本相同的情况下，用尽可能少的参数建立模型[4]，3个阶次模型都在可接受范围内。

现对3个模型进行进一步筛选。采取模型统计检验进行分析，因为建模所用氧化炉温度数据波动在0.4℃左右，故取误差标准数值e=0.4和小概率α=0.05。查阅χ2分布表可知χ2(21)=32.67，故选择接受三阶与四阶模型，考虑到数据的拟合程度，最终将氨空比模型定为四阶，模型的性能指标见表2。

表2 模型的性能指标

2.2 模型检验

由于建立的氨空比模型为参数模型，在确定模型为四阶的基础上，选择添加适当的零点。通过其相应阶跃反应的超调比及调节时间等指标确定，选择添加一个零点(加入滞后时间为3min)，最终氨(Y(z))空(U(z))比的参数模型为：

(2)

对数据进行建模的过程中，要检验模型的适用性。模型检验的实质是对模型残差序列进行白噪声检验。若残差序列非白噪声，说明一些重要信息未被提取，应重新设定模型。检测方法为：选取工况稳定下的一组数据，利用氨空比数据测取模型输出，对真实输出与模型输出的误差进行白噪声检测。模型的拟合结果如图2所示，可以看出，模型输出能够较好地反映氧化炉温度的真实变化情况。经分析可知，误差符合白噪声检验，因此模型是满足要求的。得到氨空比与氧化炉温度的传递模型后，即可利用其进行模型预测控制研究。

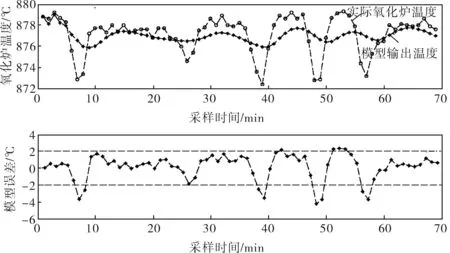
图2 模型输出、实际输出与误差曲线

3 模型预测控制

模型预测控制通常被简称为预测控制，是在建立各种不同模型的基础上，采用在线滚动优化指标与反馈自校正的策略，力求有效克服受控对象的不确定性、时滞和时变影响，从而达到预期的控制目标——参考轨迹的输入，并使系统有良好的鲁棒性和稳定性[5，6]。预测控制的结构如图3所示。

图3 预测控制结构示意图

预测控制算法一般包括3个部分，分别是模型预估、滚动优化和反馈校正。模型预估是展示系统未来动态行为的功能，任意给出未来的控制策略观察对象在不同控制策略下的输出变化，为比较这些控制策略的优劣提供依据；滚动优化不是一次离线进行，而是反复在线进行的；反馈校正可以在保持模型不变的基础上对未来误差进行预测并加以校正。

预测控制相比于传统PID算法，是一种基于对象阶跃响应的预测控制算法。传统PID算法对温度这种具有时延的控制对象不能取得良好的控制效果；而预测控制能有效解决时延问题，采用多步预估技术，并按预估输出与给定值偏差最小的二次性能指标实施控制，是目前一种最优的控制技术[5，7～10]。

3.1 模型预估

动态矩阵控制是一种基于对象阶跃响应模型的预测控制算法。动态矩阵控制利用对象阶跃响应模型作为预测控制模型来获得对象未来输出的预测值。在工艺允许的情况下，利用阶跃响应法得到响应模型。被控对象的阶跃响应采样值计算式为：

α(i)=α(iT),i=1,2,…,N

(3)

式中N——模型长度；

T——阶跃响应的采样周期；

α(i)——系统阶跃响应在该时刻的幅值。

模型在k时刻的输出是k时刻以前所有输出增量的叠加，即：

(4)

记当前时刻为k、预估步长L，如果当前和未来时刻的控制增量序列为Δu(k),Δu(k+1),…,Δu(k+L-1)，则未来时刻的输出估计为：

yM=AΔu+s

(5)

其中A由对象动态响应系数构成，是维数为P×L的矩阵，为动态矩阵，易知AΔu为当前和未来时刻的控制对输出的影响；s为过去的控制所产生的输出[11]。

3.2 反馈校正

上述模型还未加入误差与干扰，尽管模型预测输出yM(k+j)能够在k+j时刻接近期望输出yR(k+j)，却不能保证对象输出yp(k+j)，因此需要对输出预估值进行校正，从而得到更加准确的控制量。校正公式如下：

yc(k+j)=yM(k+j)+(y(k)-yM(k)),j=1,2,…,P

(6)

3.3 滚动优化

预测控制是一种最优控制策略，因为它以参考轨迹为优化目标，通过最优算法使其未来一段时间内的某项性能指标最小，控制作用序列采用预估偏差计算，但只有当前的控制作用是实际执行的。预测控制通常是在控制中设定一条参考轨迹，使输出由当前值逐步过渡到设定值。通常采用的参考轨迹为一阶指数形式，即：

yR(k)=y(k),yR(k+j)=αjy(k)+(1-αj)yS,

j=1,2,…,P

(7)

其中α=exp(-Ts/Tf)称为柔化系数，yS为过程对象的设定值。

控制算法的任务是根据输出预估值与输出期望值的偏差来计算出用以施加的控制量，使对象的输出尽可能接近期望的参考轨迹。性能指标用来表征控制算法的优劣，即：

J=eTQe+ΔuTRΔu

(8)

式中e——输出预估偏差；

Q——误差加权矩阵；

R——控制作用加权矩阵。

3.4 仿真结果

为了更准确地模拟实际工况，对过程输出与控制输出分别加入小幅波动信号。用Matlab进行仿真实验，具体参数：控制步长L=2，预测步长P=4，误差作用加权矩阵Q=0.9，控制作用加权矩阵R=0.9，一阶惯性环节时间常数Tf=10，采样时间Ts=1，模型长度N=40，过程对象设定值yS=876。所得模型输出与预测控制输出曲线如图4所示，控制误差与性能指标如图5所示，控制增量曲线如图6所示。依据实验结果比较传统PID控制与预测控制的控制效果，可见预测控制能够取得良好的控制效果，控制增量基本保持不变，稳定情况下保持在10-4数量级左右，并没有像实际现场那样存在较大波动，同时也可以看到模型能够很好地反应实际情况，性能指标也保持在0.0～0.2很小的范围内，预测控制取得了较好的控制效果。因此，预测控制能够很好地解决氧化炉温度等具有纯滞后对象的控制问题。

图4 模型输出与模型预测控制输出曲线

图5 控制误差与性能指标

图6 控制增量曲线

4 结束语

采用预测控制算法对硝酸生产中的氧化炉温度进行控制。通过OPC协议读取现场的实时数据，利用阶跃响应法求得模型的离散传递函数，并对模型的精度进行检验。利用求得的模型来模拟现场实际工况，通过仿真比较传统PID控制与预测控制的控制效果，可以看出预测控制效果在控制时延对象时能取得良好的效果。

[1] 李鑫.双加压法生产稀硝酸工艺的核心——四合一机组[J].新疆化工，2009，(4) ：20～21.

[2] 汪家铭.双加压法渐成我国硝酸生产的主流工艺[J].化学工业，2009，(6) ：73.

[3] 孙立辉.双加压法稀硝酸生产技术在我国的现状及发展[J].氮肥技术，2008，29(2) ：44～51.

[4] 李进文.选择药物动力学模型的最终预测误差准则[J].中国药理学通报，1997，(3) ：85～86.

[5] 席裕庚,李德伟,林姝.模型预测控制——现状与挑战[J].自动化学报，2013，39(3)：222～236.

[6] 李永富.基于MATLAB混合仿真平台的智能模型预测控制及其应用研究[D].天津：河北工业大学，2006.

[7] 高强,李航.基于单变量与多变量系统的模型预测控制研究[J].计算机工程与设计，2013，34(9) ：3266～3272.

[8] Li N,Li S Y,Xi Y G.Multiple Model Predictive Control for MIMO System[J].自动化学报，2003，29(4)：38～45.

[9] 刘富春,赵均,钱积新.多变量约束快速动态矩阵控制算法研究[J].浙江大学学报(工学版)，2005，39(5) ：68～71.

[10] 杨圆圆.模型模型预测控制研究与应用[D].大庆：大庆石油学院，2006.

[11] 黄德先，叶心宇,兰建敏，等.化工过程先进控制[M].北京:化学工业出版社，2006：69～108.