弹性体结构光纤光栅应变传感器的设计与性能研究

杜俊贤 王连桂

(烟台汽车工程职业学院，山东 烟台 265500)

单模光纤布拉格光栅(Fiber Bragg Grating，FBG)简称为光纤光栅，是在单模光纤上采用紫外激光照射相位掩模板写制而成的波长调制型光学无源器件，具有抗电磁干扰、体积小、易封装、与待测对象结合和易组网的特点，在航空航天设备、钢结构设施及大坝桥梁等结构的健康监测领域应用广泛[1～3]。常见的光纤光栅应变传感器封装方式为基片粘贴式、管状嵌入式及两端固定式等，基片粘贴式一般是将光纤光栅用环氧胶粘贴在钢性基板上，多用于结构表面应变的测量[4，5]；嵌入式则将光纤光栅灌封于较小的钢管中，适合于大坝等土木工程内部的应变监测[6]；两端固定式是在中间光纤光栅有良好保护的基础上，将两端粘贴固定，应变直接作用在栅区上，适合于较小尺寸场合的应用。虽然多种结构的光纤光栅应变传感器获得了大量的应用[7，8]，但传感器的高精度、稳定度和长期可靠性仍是当前研究的难点和热点。

笔者在分析当前光纤光栅应变传感器结构特点的基础上，用激光加工设计305不锈钢材料的弹性封装结构，并通过应变力学仿真和实验研究测试了传感器的灵敏度、线性度及稳定度等性能指标。

1 光纤光栅传感器的应变响应机理分析①

光纤光栅是在载氢增加光敏性后的单模光纤上，利用紫外激光照射相位掩模板形成的，成栅后在照射区域的单模光纤上光纤纤芯呈周期性调制。根据光在光纤中传输的耦合模理论，当一束光入射到光纤中时，遇到光纤光栅会有满足反射条件的窄带光反射回来[9]，反射回的窄带光波长即光纤光栅的中心波长λB，可表示为：

λB=2neffΛ

(1)

式中neff——纤芯导模的有效折射率；

Λ——折射率调制周期。

当有应力作用到光纤光栅上时，光纤光栅的中心波长变化ΔλB可表示为：

ΔλB=2(ΛΔneff+neffΔΛ)

(2)

在应力作用下，一方面由于光弹效应会引起有效折射率neff的变化，另外由直接变形引起栅格周期Λ的变化。假定在温度不变的条件下，光纤光栅的中心波长变化ΔλB(ε)与光纤光栅所受轴向应变变化Δε之间的关系可表示为：

ΔλB(ε)=kλBΔε

(3)

其中，k为应变响应的灵敏度系数，封装后传感器可通过应变测试进行标定[10，11]。可以看出，应变值与波长变化量之间存在线性关系。

2 封装设计及其力学仿真

设计模型材料使用不锈钢305(1Cr18Ni9或1Cr18Ni12Ti)，其弹性模量为190GMPa，泊松比为0.305，密度8 000kg/m3，屈服强度不小于177MPa，抗拉强度不小于480MPa，布氏硬度不大于187，伸长率不小于40%；实际屈服强度305MPa，抗拉强度630MPa，延伸率58%，维氏硬度164。弹性结构光纤光栅应变传感器封装模型的设计结构如图1所示。

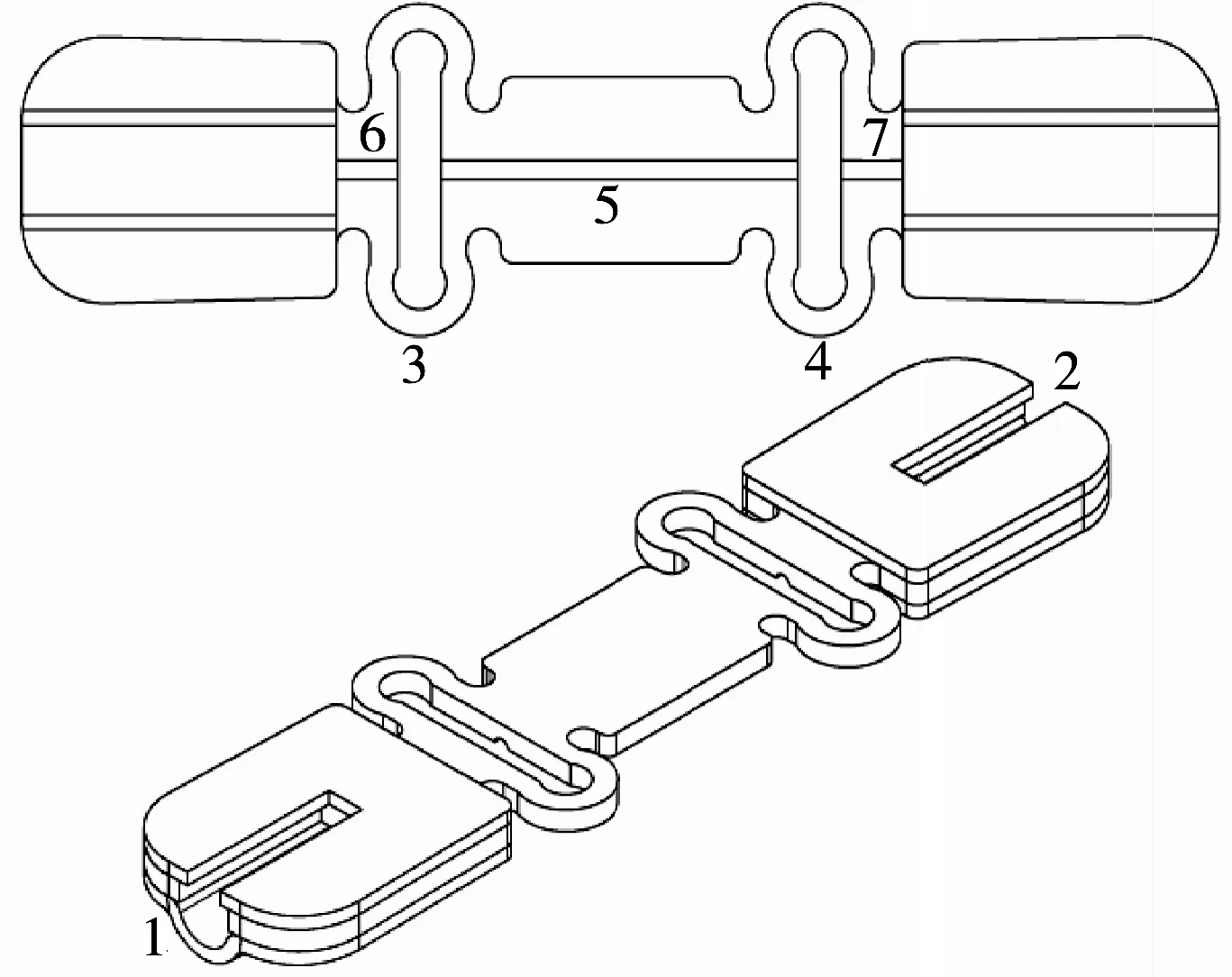
图1 弹性封装结构示意图 1、2——光纤出纤槽； 3、4——对称的弹性体结构；5——光纤光栅敏感元件放置区域；6、7——光栅两端的光纤固定点，通过环氧胶将光栅两端的光纤固定，固定光纤长度3mm

为分析其力学性能，在Ansys中建立有限元模型，如图2所示。其中，传感器A区和C区的底部粘贴在试件上，根据传感器的安装方式，将A区作为固定的一端，C区作为加力的一方，传感器根据A区和C区的相对位移来测试试件的应变。同时，根据传感器的结构，提取传感器主要应变B区域边界上的节点作为测量部位(图2的n1和n2节点)和施加力的节点n3，3个节点皆在轴线位置上。将节点n1和n2的位置差作为B区域的长度，将节点n3和n2的位置差作为A区和B区的长度。为了更好地体现小应变的模拟效果，将C区底部的节点自由度耦合在一起，其中n3为施加拉力和简谐力的节点。

图2 传感器的有限元模型

利用Ansys对传感器在-2 000～2 000με的应变响应进行仿真分析，在测量范围的边界2 000με和-2 000με下的传感器应变仿真云图分别如图3a、b所示，应力的作用主要集中在弹性体区域，且均在其弹性范围内。该结构将应变变化区域设置在弹性体上，通过弹性体的变化表征整体结构的应变，有效避免了原有基片式封装结构的整体结构变形及疲劳等问题，同时提高了传感器的使用寿命。在应用于应变检测时，待测点的应变通过弹性结构传递到封装于其上的光纤光栅敏感元件，进而引起光纤光栅中心波长的变化。在传感器标定后，即可通过检测波长变化反演测点的应变情况。

图3 传感器应变仿真云图

根据设计尺寸，用激光加工技术在厚度为2mm的305不锈钢板材上，加工弹性体结构光纤光栅应变传感器封装结构，在加工过程中需要注意保持板材的平整性和外力自由性，以保证弹性体的良好性能。

3 性能测试

选取中心波长1 551.300nm、栅区长10mm、3dB带宽0.250nm的光纤光栅，并为检测负向应变施加预应力将该光纤光栅的波长预拉伸至1 553.300nm，采用环氧胶将光栅的两端固定于传感器的6和7固定点(图1)，保持48h使环氧胶固化，保持良好的稳定度。然后，将设计的光纤光栅应变传感器焊接固定在等应变梁上，利用高精度光纤光栅解调仪SM125读取光纤光栅应变传感器的中心波长。同时在等应变位置布设一个高精度电子应变计，通过增减砝码调整等应变梁产生应变的大小。

首先进行正向应变实验，传感器位于等应变量的上表面，通过增减砝码，根据高精度应变计的读数设定应变值分别为100、200、300、500、800、1 000με，然后将等应变梁反置，对应光纤光栅应变传感器感受到的应变值分别为-100、-200、-300、-500、-800、-1 000με。实验测得应变传感器光纤光栅的波长与应变的关系如图4所示，传感器的应变灵敏度为1.21pm/με，线性度达0.999 6，可以推得其检测精度不大于1με。

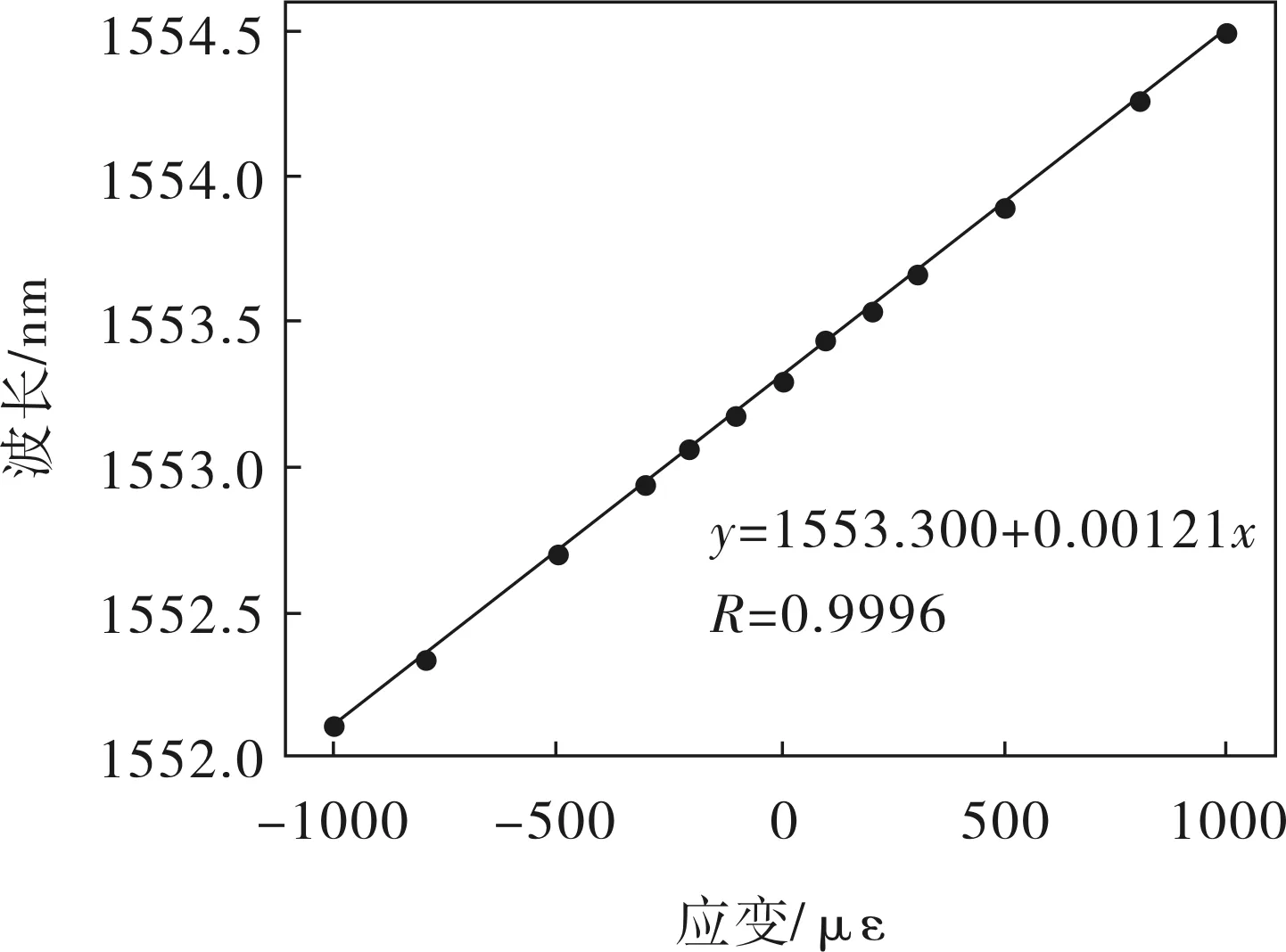
图4 光纤光栅传感器波长与应变的关系

另外，设定等应变梁的应变值为500με，对其进行1h的稳定度测试，每秒钟读取一个光纤光栅传感器的波长，并将其用灵敏度关系式转换为应变值，实验数据如图5所示，其长期测试稳定度不大于±3με，相对稳度0.3%，满足结构健康监测对高精度应变传感器稳定度小于0.5%的要求。

图5 光纤光栅应变传感器稳定度测试

4 结束语

基于弹性体结构设计的新型光纤光栅应变传感器结构，能够使应变有效地传递到光纤光栅敏感原件，实验测试获得了良好的应变响应线性度、 灵敏度和稳定度。通过对弹性体尺寸的改变，可以设计应变灵敏度不同的传感器，为传感器的增敏封装提供了新的思路，同时在实际应用中具有良好的应用前景。值得一提的是，封装后的光纤光栅应变传感器根据光纤光栅对外界参量的敏感机理，除了受应变的影响之外还会受到温度的影响，在使用时需要增加温度补偿光栅，消除温度的影响，保证应变检测的独立性。

[1] 李硕,黄俊斌,顾宏灿,等.基于光纤光栅应变传感器的潜艇结构监测系统[J].舰船科学与技术,2012,34(2):77～80.

[2] 舒岳阶,陈伟民,章鹏,等.光纤布喇格光栅器件应力疲劳评价理论研究[J].光子学报,2013,42(7):807～811.

[3] 张权,丁克勤,李德桥.一种钛合金基片封装的光纤光栅应变传感器[J].光电技术应用,2010,25(3):33～35.

[4] 刘春红,赵印明,陈爽,等.封装材料对光纤光栅应变传感器的影响[J].航空精密制造技术,2010,46(3):50～52.

[5] 张桂花,柴敬,李旭娟,等.基片式光纤光栅应变传感器的应变传递研究[J].激光与光电子学进展,2014,51(1):1～6.

[6] 孙丽,梁德志,李宏男.管式封装FBG应变传感器应变传递率影响因素分析[J].沈阳建筑大学学报(自然科学版),2007,23(6):881～885.

[7] 曾克.光纤光栅应变传感器在地址灾害上的应用[J].物探与化探,2014,38(1):142～144.

[8] 梁磊,王艳妮,刘德力.粘贴式光纤光栅应变传感器的应变传递分析[J].武汉理工大学学报,2008,30(10):144～146.

[9] 陈显,余尚江,林明,等.一种复合材料封装光纤光栅片式应变传感器研究[J].传感器与微系统,2008,27(12):43～44.

[10] 袁子琳,龚元,马耀远,等.光纤布喇格光栅应变传感器结构优化研究[J].光子学报,2012,41(11):1261～1266.

[11] 张兆亭,闫连山,王平,等.基于光纤光栅的钢轨应变测量关键技术研究[J].铁道学报,2012,34(5):65～69.

DesignandPerformanceStudyofFBGStrainSensorwithElasticBodyStructure

DU Jun-xian, WANG Lian-gui