一种基于熵的WBCT自适应方向分解优化算法
唐国维 张 岩 王苫社 李井辉
(1.东北石油大学计算机与信息技术学院,黑龙江 大庆 163318;2.哈尔滨工业大学计算机科学与技术学院,哈尔滨 150001)
从傅里叶分析到小波分析再到多尺度几何分析(Multiscale Geometric Analysis,MGA),多年来数学工作者和信号处理专家一直试图寻找更有效的信号表示和分析方法。在过去的几十年中,小波分析的快速发展和成熟无疑使信号处理工作达到了一次高潮,其应用领域也迅速从数学、信号处理拓展到物理、天文、地理、生物及化学等学科。尽管如此,研究者们也发现,由于小波变换只能反映信号的零维奇异性,即只能表达奇异点的位置和特性,而对于更高维的特征则显得力不从心。另外,由于小波变换核为各向同性(isotropy),因而只能表达图像过边缘的特性,无法表达图像沿边缘的特性。因此小波在表示具有点奇异性的函数时是最优基,但是对于自然图像而言,小波基并不是最优基[1]。
约十年前,出现了一门崭新的信号分析工具——多尺度几何分析[2]。多尺度几何分析包括一系列的方法,主要有:Candès E J和Donoho D于1998年提出的脊波变换(Ridgelet Transform)、1999年提出的单尺度脊波变换(Monoscale Ridgelet Transform)和Curvelet变换,Pennec E L和Mallat S于2000年提出的Bandelet变换及Do M N和Vetterli M于2002年提出的Contourlet变换等。其中,Contourlet变换是一种基于多分辨率多方向的几何分析方法,能够较好地捕捉图像本身所特有的几何特性[3],其基本思想是首先利用一个类似于小波的多尺度分解捕捉边缘奇异点,再根据方向信息将临近的奇异点连接成轮廓,且使用一个系数表示。但由于变换中使用了LP变换,使得Contourlet变换本身并不适合直接用于图像编码等处理。
为解决Contourlet变换中的冗余问题,Eslami R和Radha H提出了基于小波的Contourlet变换(Wavelet-Based Contourlet Transform,WBCT)[4]。该方法去除了LP滤波器结构引入的数据冗余,形成了非冗余且完全重构的滤波器组,能够有效地逼近图像。相比于Contourlet,WBCT更适合于图像压缩。但是,WBCT在进行方向分解的时,为避免能量流失,对最低频子带未进行方向分解;而对高频子带,采取不同子带方向分解数目固定的分解方式,没有充分考虑图像本身的特性。特别是高频子带通常包含大量细节信息,这给编码等后续操作带来直接影响。因此笔者提出一种基于熵的WBCT自适应方向分解优化算法,在对图像进行L级小波完全分解的基础上,对i(1≤i≤L)级高频子带进行2L-i+1个方向分解,然后分析各子带不同方向分解数目时熵的变化情况,并根据最小熵原则给出各个子带的最优方向分解数目。
1 基于小波的Contourlet变换①
Contourlet变换是在Curvelet变换的基础上提出的一种多分辨率、多方向、局域的几何分析方法,由于变换中使用了LP变换,在处理高频信息时没有进行下采样操作,导致Contourlet存在1/3的冗余。为此,Eslami R和Radha H提出了基于小波的Contourlet变换,其基本思想是用小波变换中的Mallat塔式分解代替Contourlet变换中的LP分解,从而消除了Contourlet变换中存在的冗余,这一过程用可分离的滤波器组实现。然后用方向滤波器分别对Mallat分解中的非LL子带进行卷积处理,以更“稀疏”地表示图像,这一过程由不可分离的具有迭代层次结构的扇形滤波器组实现,其原理如图1所示。
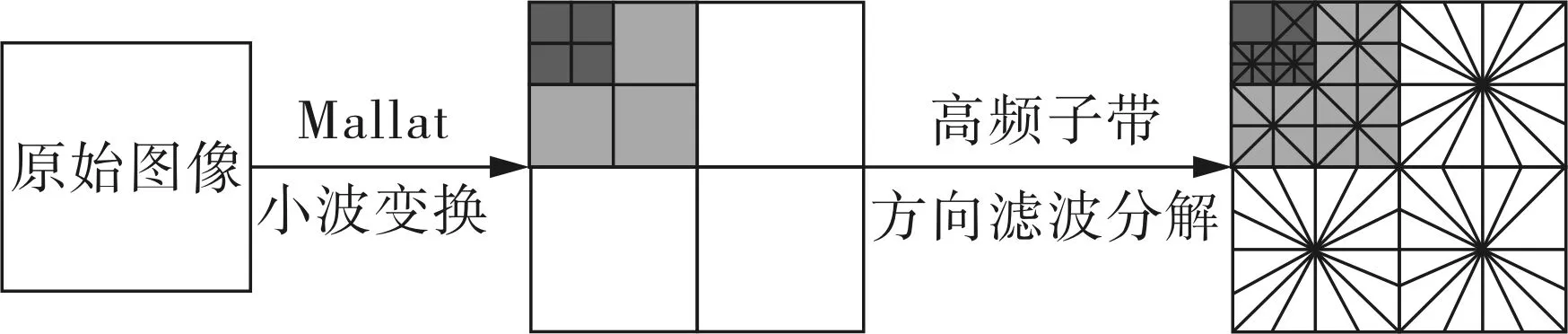
图1 WBCT方向分解原理
对于高频细节部分的方向分解,WBCT采用了与Contourlet相同的方法,即将高频部分分解于各个频带方向上,每一层频域分解成2l个子带。图2给出了八方向的频域子带分解示意图,与ω0轴正方向夹角45~135°之间的频带称作第一通道,其余为第二通道。
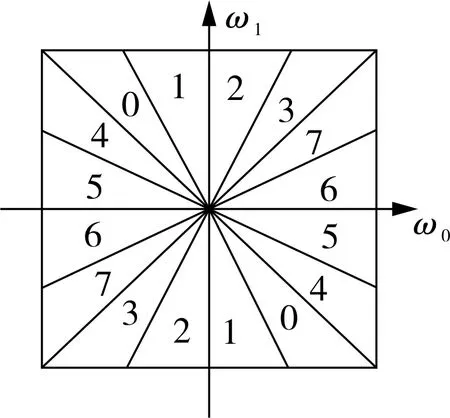
图2 楔型频域子带分解
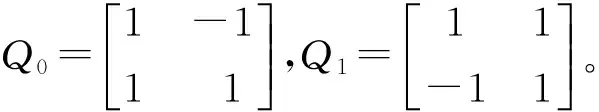
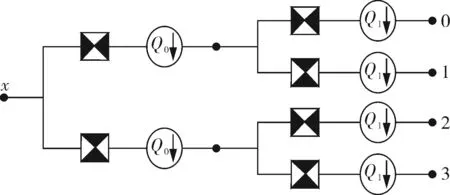
图3 四方向滤波器组示意图
WBCT继承了小波变换和Contourlet变换的优点,同时又弥补了二者的不足,从而更容易捕捉图像的几何结构和纹理特性。图4给出了Babara图像的DWT系数和WBCT系数的对比,从中可看出Contourlet的方向滤波对小波系数高频部分的纹理捕捉能力。

图4 Babara图像的DWT系数和WBCT系数分布
2 基于熵的自适应方向优化分解
在进行方向分解的时候,考虑到低频分量的特殊地位,WBCT对最低频子带不进行方向分解,而对高频子带采取不同子带的方向分解数目固定的分解方式。由于高频子带包含丰富的细节信息,方向分解数目合适与否将对后续处理(如编码等)产生较大影响。笔者以PSNR值对其特性进行分析。对512×512的Babara图像进行4级小波变换,并对高频子带按不同方向分解数目进行方向分解,然后采用SPECK算法[5]对其进行压缩处理,并计算重构图像的PSNR值。表1给出了码率为0.25b/p时的PSNR值。

表1 Babara图像各高频子带不同方向分解数的PSNR值对比
从表1中可以看出,对高频子带进行不同数目的方向分解,压缩后其重构图像PSNR值是不同的,因此如何确定高频子带最佳方向分解数目是一个值得研究的问题。理论上可通过计算变换域迭代投影过程中图像的量化误差并使其最小而得到,但该方法的实际操作性差[6]。文献[7]结合实验,给出了如下的方向分解策略:对原始图像进行L级小波分解以后,仅在除第L级和第L-1级外的各级小波子带上进行方向分解,且最高分辨率上方向分解数为2L-1。显然该方法对图像内容还考虑得不够深入。笔者紧密结合图像自身特性,从熵的角度对方向分解数目进行研究。
根据文献[8,9],描述高频子带纹理/边缘特征的一个重要指标是熵。由于Contourlet根据方向信息将临近的奇异点连接成轮廓,且使用一个系数表示,因此方向分解必然引起子带熵的变化,而且变化和分解的方向数目有关。根据熵的定义,如果方向分解后小波系数分布更加有规律(对编码有利),其熵值必定减小。因此,最佳的方向分解数应使小波子带的熵达到最小值。
设s为经Contourlet方向分解后的任一子带,则定义该方向子带的熵如下:
Es=-∑p(i)log2p(i)
(1)
其中,p(i)为像素灰度值为i的概率,p(i)=ni/ns,ni为灰度值为i的像素数目,ns为子带s的像素总数。当对小波子带进行不同数目的方向分解时,其熵值发生变化。熵值变大,表明有轮廓被打散;熵值变小,则表明有系数被合并成为轮廓。为此,对某一小波高频子带S,若其方向分解数目为2d,d=0,1,2,…,则定义该小波子带的平均熵为:
(2)
其中,Es(s=1,2,…,2d)为Contourlet方向分解后的各子带熵。则基于熵的Contourlet方向分解优化过程如下:
a. 小波子带完全方向分解,即假定对图像进行L级小波变换,则对第i(1≤i≤L)级高频子带确定其首次方向分解数为2L-i+1;
b. 确定最佳方向分解数;
c. 对所有高频小波子带均进行步骤b的处理。
假设对某一小波子带S进行2j个方向分解,步骤b的具体方法为:
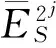
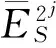
3 方向分解和压缩实验
3.1 方向分解实验
为验证上述算法的有效性,选取512×512的标准灰度图像Boat进行方向分解实验。小波基选取D9/7双正交小波基,分解级数L=4。考虑到pkva滤波器在定位边缘方向上更加有效,因此在进行方向分解时采用pkva滤波器取代扇形滤波器以减少方向间的交互信息。按照式(1)计算得到小波分解各高频子带的熵见表2。
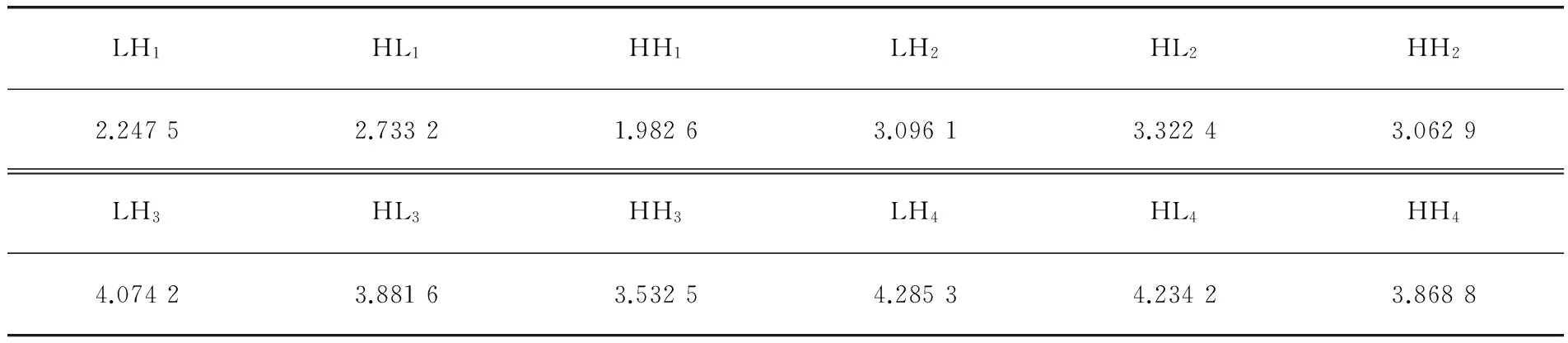
表2 Boat图像小波分解后各高频子带的熵
对各小波高频子带采取不同的方向分解数进行方向分解,并按式(2)计算每个小波子带不同方向分解数时的平均熵,计算结果见表3,并按最小熵原则确定最佳方向分解数目。

表3 Boat图像各高频子带不同方向分解数时的平均熵
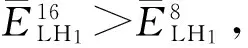

表4 Boat图像两种算法下各子带的方向分解数
图5给出了根据原始WBCT和笔者改进的算法进行的实际方向分解的情况,后者系数分布规律更加合理,更有利于后续进一步编码处理。
3.2 图像编码压缩实验
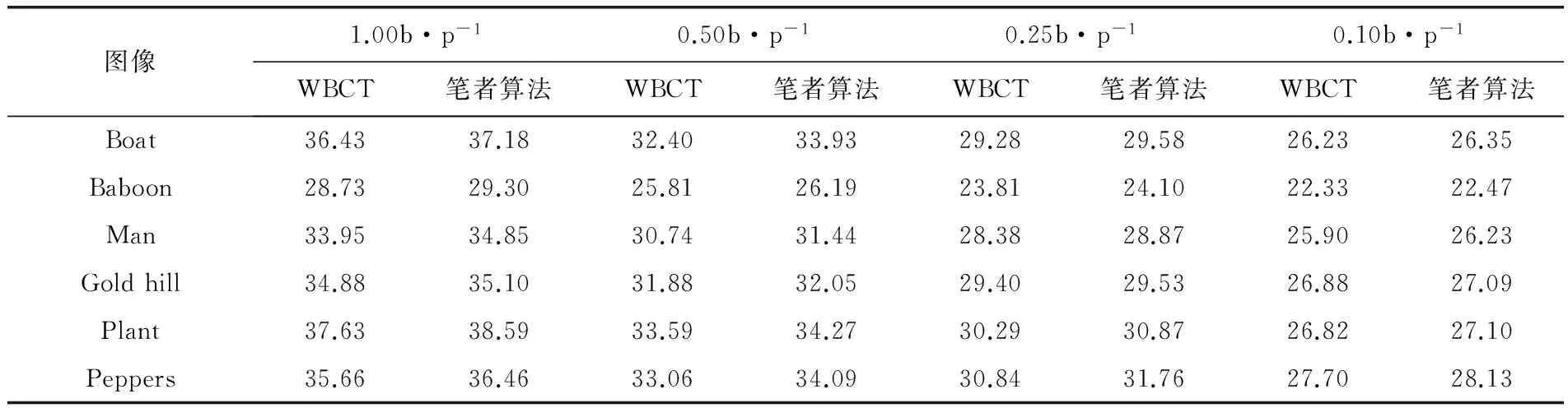
为验证方向分解的合理性,选取Boat等6幅常用标准图像,采用SPECK算法对方向分解后的图像进行压缩处理,并计算其重构图像的PSNR值(表5)。可以看出,与原始WBCT算法方向分解数目固定相比,笔者提出的最优方向分解数算法可以明显提高重构图像的峰值信噪比。

图5 Boat图像两种算法方向分解情况对比表5 采用SPECK算法压缩后不同码率下的PSNR值
图像1.00b·p-10.50b·p-10.25b·p-10.10b·p-1WBCT笔者算法WBCT笔者算法WBCT笔者算法WBCT笔者算法Boat36.4337.1832.4033.9329.2829.5826.2326.35Baboon28.7329.3025.8126.1923.8124.1022.3322.47Man33.9534.8530.7431.4428.3828.8725.9026.23Goldhill34.8835.1031.8832.0529.4029.5326.8827.09Plant37.6338.5933.5934.2730.2930.8726.8227.10Peppers35.6636.4633.0634.0930.8431.7627.7028.13
4 结束语
Contourlet变换将小波的优点延伸到高维空间,具有多分辨率、局部化及各向异性等优良特性,是一种真正意义上的图像二维表示方法。笔者针对基于小波的Contourlet方向分解没有考虑子带内系数分布特性的问题,提出基于熵的子带方向分解优化算法,使得各方向子带内部的局部相关性加强,而子带间相关性减弱,这对提高图像的压缩比是至关重要的。通过实验可以看出,重构图像的峰值信噪比得到有效提高,这说明笔者将熵作为方向分解的依据是正确的。
[1] 倪伟,郭宝,龙杨锣.图像多尺度几何分析新进展:Contourlet[J].计算机科学,2006,33(2):234~236,262.
[2] 焦李成,谭山.图像的多尺度几何分析:回顾和展望[J].电子学报,2003,31(z1):1975~1981.
[3] Do M N,Vetterli M.Contourlets:A Directional Multiresolution Image Representation[C].Proceedings of IEEE International Conference on Image Processing.New York,USA:IEEE,2002:357~360.
[4] Eslami R,Radha H.Wavelet-based Contourlet Transform and Its Application to Image Coding[C].Proceedings of IEEE International Conference on Image Processing.Singapore:IEEE,2004:3189~3192.
[5] Pearlman W A,Islam A,Nagaraj N,et al.Efficient,Low-complexity Image Coding with a Set-partitioning Embedded Block Coder[J].IEEE Transactions on Circuits and Systems for Video Technology,2004,14(11):1219~1235.
[6] 唐国维.嵌入式小波图像编码算法及应用研究[D].哈尔滨:哈尔滨工程大学,2010.
[7] 王向阳,左珂可.低比特率混合域图像压缩编码算法研究[J].中国图象图形学报,2007,12(11):2000~2005.
[8] Pham T D.Image Texture Analysis Using Geostatistical Information Entropy[C].The 6th IEEE International Conference on Intelligent Systems (IS).Sofia:IEEE,2012:353~356.
[9] Pham T D. Geostatistical Entropy for Texture Analysis:An Indicator Kriging Approach[J].International Journal of Intelligent Systems,2014,29(3): 253~265.

