Asymptotic Behavior of the Drift Coefficient Estimator of Stochastic Differential Equations Driven by Small Noises

SHEN Liang (沈 亮), XU Qing-song (许青松)

1 School of Mathematics and Statistics, Central South University, Changsha 410075, China 2 School of Science, Linyi University, Linyi 276005, China

Asymptotic Behavior of the Drift Coefficient Estimator of Stochastic Differential Equations Driven by Small Noises

SHEN Liang (沈 亮)1, 2*, XU Qing-song (许青松)1

1SchoolofMathematicsandStatistics,CentralSouthUniversity,Changsha410075,China2SchoolofScience,LinyiUniversity,Linyi276005,China

The parametric estimation problem for diffusion processes with small white noise based on continuous time observations is well developed. However, in parametric inference, it is more realistic and interesting to consider asymptotic estimation for diffusion processes based on discrete observations. The least squares method is used to obtain the estimator of the drift parameter for stochastic differential equations (SDEs) driven by general Lévy noises when the process is observed discretely. Its strong consistency and the rate of convergence of the squares estimator are studied under some regularity conditions.

stochasticdifferentialequations(SDEs);consistency;leastsquaresestimator(LSE);discreteobservations;noises

Introduction

Stochastic differential equations (SDEs) are differential equations which subject to additive “white noise” and related random disturbances. A solution of an SDE is a stochastic process. SDEs are being extensively used for modeling uncertain dynamic phenomena in various applications such as biology, medicine, econometrics, finance, geophysics and oceanography. Although it is often easy to form an SDE which models the dynamic phenomenon in hand, in practice, the parameters of the SDE model remain uncertain or completely unknown. The parameters may be, for example, physical constants related to the environment or densities of fluctuations (noise variances, volatilities) in the phenomenon. Therefore parameter estimation in SDE models is a crucial area in many applications where SDEs are used. For a more recent comprehensive discussion, we refer to Refs. [1-2].

The parametric estimation problem for diffusion processes with small white noise based on continuous time observations is well developed and it has been studied by many authors[3-4]. There have been many applications of small noise in mathematical finance, see Refs. [5-8]. In parametric inference, due to the impossibility of observing diffusions continuously throughout a time interval, it is more practical and interesting to consider asymptotic estimation for diffusion processes with small noise based on discrete sampling data.

Dd={t0, t1, …, tn; X(t0), X(t1), …, X(tn)}.

In this direction, there has been made substantial progress. Sørensen[9]used martingale estimating function to establish consistency and asymptotic normality of the estimators of drift and diffusion coefficient parameters whenε→0 andnis fixed. Sørensenetal.[10-11]used a contrast function to study the efficient estimation for unknown parameters in both drift and diffusion coefficient functions. Baltazar-Larios and Sørensen[12]proposed a method for obtaining the maximum likelihood estimates of parameters in diffusion models when facing discrete time samples of the integral of the process. Uchida[13]used the martingale estimating function approach to study the estimation of drift parameters for small diffusions under weaker conditions. Long[14]had started the study on parameter estimation for a class of SDEs driven by small stable noise. However, there have few results on parametric inference for stochastic processes with small Lévy noises yet.

Ideally, parameter estimation for diffusion processes of discrete-time observations should be based on the likelihood function. Unfortunately, the transition densities are usually unknown except some special case. In order to overcome this difficulty, the least squares method has been proposed by Kasonga[15]and Le Breton[16]. Giovannietal.[17]studied some applications of the least squares method to differential equations and related problems. So, it is interesting in studying of parameter estimation for the following SDEs by using least squares method. Here the SDEs are driven by more general Lévy noise based on discrete observations.

1 Preliminaries

(1)

wheref:→andg:→are known functions anda,bare known constants.évy motion independent of {Bt,t≥0}, withZ1～Sα(1,β, 0) for β∈[0, 1], 1<α<2.

(2)

Then, we get

(3)

DenoteCas a generic constant whose value may vary from place to place.

The following regularity conditions are assumed to hold.

(A1) The functionsf(x) andg(x) satisfy the Lipschitz conditions, that is, there exists a constantL>0 such that

(A2) There exist constantsM>0 andr≥0 satisfying the growth condition

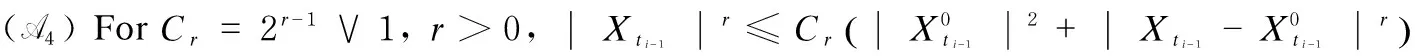
2 Consistency of the Least Squares Estimator (LSE)

To obtain the LSE, introduce the following contrast function

(4)

(5)

The underlying lemma due to Long[14]is one of the important tools which will be used later.

Lemma 1 Under conditions (A1)-(A2), whenε→0, we have

(6)

Proposition 1 Under conditions (A1)-(A3) one has that

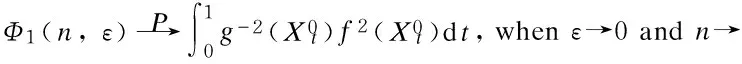
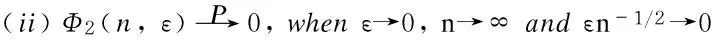
Proof The results (i) and (iii) of Proposition 1 can be directly obtained by Long[14]. And we can also obtain that

P(Φ3(n, ε)>δ)≤O(εn(α -1)/α).

(7)

Now to prove (ii), for ti-1≤t≤ti, i=1, 2, …, n,

(8)

By using Gronwall inequality, then

(9)

which yields that

(10)

thus,

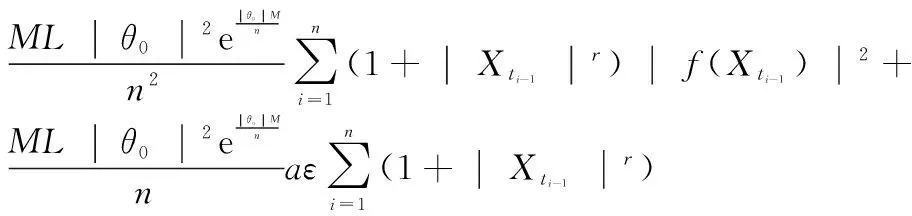
Φ2, 1(n, ε)+Φ2, 2(n, ε)+Φ2, 3(n, ε).

(11)

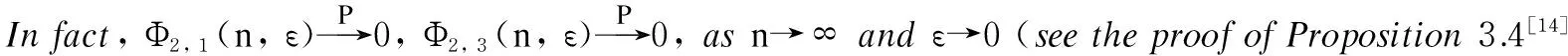
Then, onlyΦ2, 2(n,ε) could be considered,

(12)

By the Markov inequality and Ito’s isometry property, for any givenη>0,

(13)

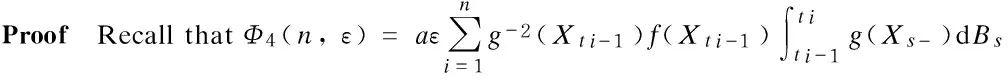
Byusing(A1), (A3) and (A4), the following can be obtained

(14)

For any givenη>0, using the Markov inequality and Ito’s isometry property,

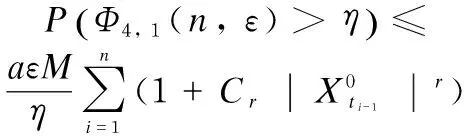
(15)

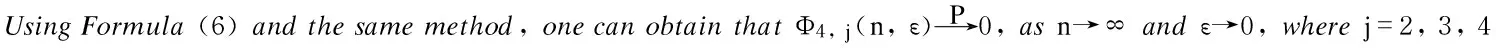
Proof By using Propositions 1 and 2, it can be obtained that

Then immediately,

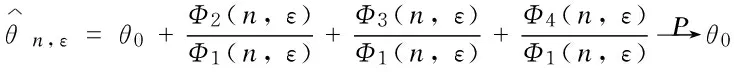
3 Conclusions

The least squares method is used to obtain the estimator of the drift parameter for SDEs driven by general Lévy noises when the process is observed discretely. Its strong consistency and the rate of convergence of the squares estimator are studied under some regularity conditions. It is also possible to use other methods such as approximate likelihood method, martingale estimating function method to study parameter estimation for SDEs driven by small Lévy noises. We expect to obtain some new and interesting results in this direction.

[1] Prakasa Rao B L S. Statistical Inference for Diffusion Type Processes: Kendall’s Library of Statistics 8 [M]. New York: Wiley, 1999.

[2] Kutoyants Y A. Statistical Inference for Ergodic Diffusion Processes[M]. Berlin: Springer, 2004.

[3] Uchida M, Yoshida N. Asymptotic Expansion for Small Diffusions Applied to Option Pricing [J].StatisticalInferenceStochasticProcess, 2004, 7(3): 189-223.

[4] Kwok S F. Langevin Equation with Multiplicative White Noise: Transformation of Diffusion Processes into the Wiener Process in Different Prescriptions[J].AnnalsofPhysics, 2012, 327(8): 1989-1997.

[5] Fujii M, Shimada Y, Takahashi A. A Market Model of Interest Rates with Dynamic Basis Spreads in the Presence of Collateral and Multiple Currencies[J].Wilmott, 2011, 54(2): 61-73.

[6] Hoffmann M. Statistical Methods for Stochastic Differential Equations[J].Chance, 2013, 26(3): 57-58.

[7] Takahashi A, Yoshida N. An Asymptotic Expansion Scheme for Optimal Investment Problems[J].StatisticalInferenceStochasticProcess, 2004, 7(2): 153-188.

[8] Kunitomo N, Takahashi A. The Asymptotic Expansion Approach to the Valuation of Interest Rate Contingent Claims[J].MathematicalFinance, 2001, 11(1): 117-151.

[9] Sørensen M. Estimating Functions for Diffusion-Type Processes[J].StatisticalMethodsforStochasticDifferentialEquations, 2012, 124(5): 1-107.

[10] Sørensen M, Uchida M. Small Diffusion Asymptotics for Discretely Sampled Stochastic Differential Equations[J].Bernoulli, 2003, 9(6): 1051-1069.

[11] Gloter A, Sørensen M. Estimation for Stochastic Differential Equations with a Small Diffusion Coefficient[J].StochasticProcessesandTheirApplications, 2009, 119(3): 679-699.

[12] Baltazar-Larios F, Sørensen M. Maximum Likelihood Estimation for Integrated Diffusion Processes[J].ContemporaryQuantitativeFinance, 2010, 10(3): 407-423.

[13] Uchida M. Estimation for Discretely Observed Small Diffusions Based on Approximate Martingale Estimating Functions[J].ScandinavianJournalofStatistics, 2004, 31(4): 553-566.

[14] Long H W. Parameter Estimation for a Class of Stochastic Differential Equations Driven by Small Stable Noises from Discrete Observation[J].ActaMathematicaScientia, 2010, 30(3): 645-663.

[15] Kasonga R A. The Consistency of a Non-linear Least Squares Estimator from Diffusion Processes[J].StochasticProcessesandTheirApplications, 1988, 30(2): 263-275.

[16] Le Breton A. On Continuous and Discrete Sampling for Parameter Estimation in Diffusion Type Processes[J].StochasticSystems:Modeling,IdentificationandOptimization, 1976, 5(4): 124-144.

[17] Giovanni B, Federica C, Mauro M. Some Applications of the Least Squares Method to Differential Equations and Related Problems[J].SingularitiesinNonlinearEvolutionPhenomenaandApplications, 2009, 9(2): 59-87.

O211.64 Document code: A

1672-5220(2015)01-0019-04

Received date: 2013-11-27

* Correspondence should be addressed to SHEN Liang, E-mail: csushenliang@126.com