盾构隧道接缝对结构内力的影响研究

陶 斌

（山西省交通科学研究院，山西 太原 030006）

1 概述

盾构法隧道结构一般是由管片拼装而成的。由于相邻管片之间的接缝处需设置防水密封垫沟槽、嵌缝槽、倒角等构造措施，因而接缝处的刚度较小，也削弱了结构的整体刚度、改变了局部应力状态，使结构的计算模型也更为复杂。不同时期世界各国的学者对盾构隧道衬砌结构设计理论和接缝的计算模拟进行了系统的研究与发展[1]。由于修正惯用计算法和梁-弹簧模型基本能体现结构的主要受力特征，且使用方便，因此成为我国盾构隧道横向计算中最常用的方法。

图1为修正惯用计算法的荷载系统，垂直方向的地基抗力假定为均布荷载，水平方向的地基抗力则假定为自由环顶部向左右45°～135°区间的均布荷载（三角形）。由于在错缝拼装时，弯矩并不是全部都由管片接缝传递，其中一部分弯矩通过环之间的剪切阻力传递给相邻环（见图2）。因此，通过对比研究试验结果和计算结果的差别，引入了弯曲刚度有效率η和弯矩提高率ξ，来评价结构的整体刚度与接缝处的内力。

图1 惯用法/修正惯用法荷载系统

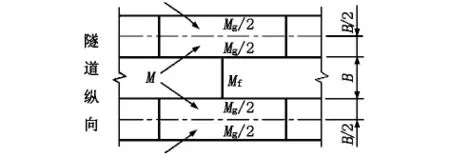
图2 错缝拼装弯矩传递及分配示意图

梁-弹簧模型是将管片主截面简化为曲梁或直梁，将管片接头模拟为转动弹簧，将管片环接头模拟为剪切弹簧，用以考虑由于接头引起的衬砌环刚度降低和错缝拼装效应的一种计算方法。梁-弹簧模型用转动刚度（Kθ）来描述管片接头的性能，对于纵向螺栓的剪力传递通过设置剪切弹簧（径向剪切刚度Kn和切向剪切刚度Kt）来实现，具体模型如图3所示。管片接头间各弹簧的转动刚度由试验或经验确定。

上述两个计算模型中的主要参数——修正惯用计算法中的刚度有效率η和弯矩提高率ξ以及梁-弹簧模型中的接头转动刚度Kθ，需经试验确定。众多试验表明[2]，接缝刚度与接缝处的轴力、弯矩有关。由于试验时基本按照接缝的实际构造进行，因此可以认为试验结果基本能够正确体现接缝刚度与内力的关系，如将接缝原型试验结果用于修正惯用计算法和梁-弹簧模型中，则计算结果的可信度较高（否则达不到理想效果）。但正是由于试验只针对一种接缝构造，因此也就很少探究接缝构造对刚度的影响。同时，在设计方案比较阶段，对每一种接缝方案均进行原型试验是不现实的。

为此，本文探讨了计算模型中如何考虑接缝构造的影响，以及如何通过改变接缝的构造达到优化调整隧道结构内力的目的。

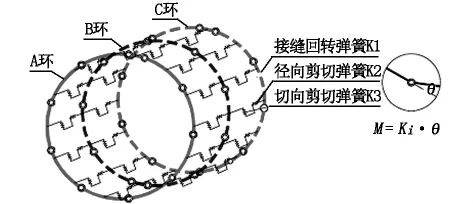
图3 梁-弹簧模型示意图

2 接缝构造对内力影响机理

2.1 管片接缝常用构造

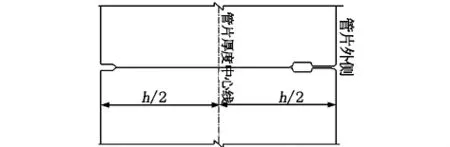
图4 常用的管片接缝构造图

盾构隧道管片接缝的常用构造如图4所示。接缝必须满足以下两个方面的要求：一是防水性能要求，二是受力与传力的要求。在防水构造方面，其型式较为固定，一般均是在接缝外侧设置防水密封垫沟槽，在沟槽内安装防水密封垫，通过密封垫的挤压进行防水。对于无榫槽构造，直接利用混凝土接触面传递弯矩、轴力、剪力。混凝土接触面的大小及其偏离管片厚度中心线的程度对内力将会产生一定的影响。

2.2 接缝构造对内力影响的机理分析

图5 直梁中部有无缺口对内力的影响

如图5所示，对于底部固定的等截面直梁，当其顶部截面中心作用一压力时，梁上无弯矩分布；但当直梁中部有偏心缺口时，将产生一定的弯矩，且弯矩的大小与缺口的偏心方向和偏心程度有关。

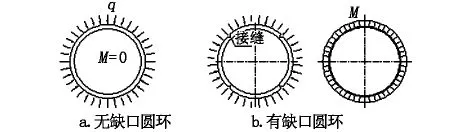
图6 圆环有无缺口对内力的影响

如图6所示，对于等截面圆环，当外周作用匀布的压力时，圆环只有轴力而无弯矩；但当圆环设置均匀对称分布的4个偏心缺口时，将产生一定的弯矩，且弯矩的大小与缺口的偏心方向和偏心程度有关。

3 考虑接缝构造的改进计算模型

根据上述机理分析，采用目前常用的修正惯用计算法或梁-弹簧模型进行盾构隧道结构内力分析时，为考虑接缝构造的影响，较好的办法是调整每块管片的计算轴线，即根据衬砌环的设计分块方式。将每块管片两侧接缝处的混凝土接触面的形心作为单元梁的节点，将每块管片厚度中线的圆弧中心也作为单元梁的节点，再将该3个节点采用圆弧拟合，以此圆弧作为该块管片的计算轴线，如图7。

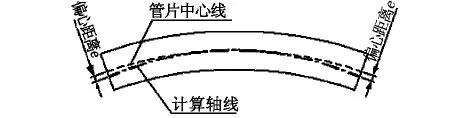
图7 无榫槽接缝的计算轴线拟合示意

4 接缝构造对结构内力影响分析

盾构隧道衬砌环弯矩一般拱顶处为最大正弯矩区，两侧为最大负弯矩区，且负弯矩绝对值小于正弯矩值。如果接缝偏心产生的附加负弯矩出现在拱顶，则可以降低衬砌环最大正弯矩的值，从而可以起到优化结构内力的效果。

4.1 无榫槽接缝构造的案例分析

某超大直径水下盾构隧道内径13.3 m，外径14.5 m，管片厚0.6 m，环宽2.0 m，衬砌环采用9＋1分块方式，其中封顶块圆弧角度为其他块的1/3。接缝处为无榫槽构造，混凝土接触面的形心位于管片厚度中心线内侧39 mm（见图4）。

以该隧道所穿越的代表性断面之一为例，对模型改进前后的计算内力对比如下。

4.1.1 采用修正惯用计算法分析

常用的修正惯用计算法得到的结构弯矩与轴力如图8所示。当考虑接缝构造的偏心影响时，将接缝对称设置在拱顶两侧，计算轴线进行拟合后，由修正惯用计算法得到的结构弯矩与轴力如图9所示。对比可知，采用改进后的模型后，隧道最大正弯矩由1 215 kN·m/环减少至 1 153 kN·m/环；对应的轴力为3 413 kN和3 408 kN，基本相同。隧道最大负弯矩由637 kN·m/环增大至705 kN·m/环，对应的轴力为4 546 kN和4 544 kN，基本相同。最大正负弯矩比由1.91减少至1.64，接缝构造对内力的调整具有较明显的效果。

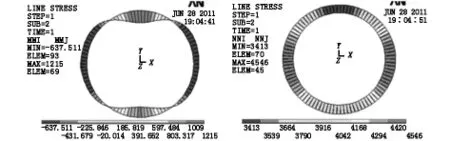
图8 不考虑接缝构造影响的结构内力图

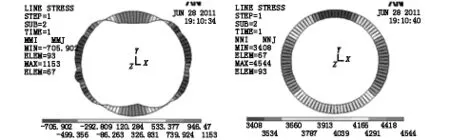
图9 接缝在拱顶两侧时结构内力图

当接缝恰好设置在拱顶时，拟合后的计算轴线得到的结构弯矩与轴力如图10所示。与不考虑接缝影响计算结果对比可知，此时隧道最大正弯矩由1 215 kN·m/环增大至 1 334 kN·m/环；最大负弯矩由637 kN·m/环增大至742 kN·m/环；衬砌环轴力基本不变，接缝的构造同样对内力产生了一定的影响。

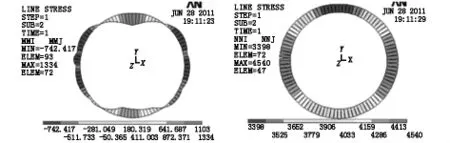
图10 接缝在拱顶时结构内力

4.1.2 采用梁-弹簧模型分析

常用的梁-弹簧模型得到的结构弯矩与轴力如图11所示。考虑接缝构造的影响，拟合轴线计算得到的结构弯矩与轴力如图12和图13所示。对比可知，采用改进后的模型，当接缝避开拱顶时，隧道最大正弯矩由1 199 kN·m/环减少至1 070 kN·m/环，最大负弯矩由708 kN·m/环增至714 kN·m/环，对应的轴力基本相同；正负弯矩比由1.69减少至1.49。

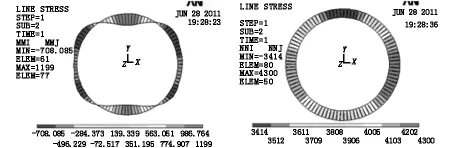
图11 不考虑接缝构造影响的结构内力

当接缝正在拱顶时，隧道最大正弯矩由1 199 kN·m/环增大至 1 279 kN·m/环，最大负弯矩由708 kN·/m环增大至847 kN·m/环，对应的轴力基本相同。

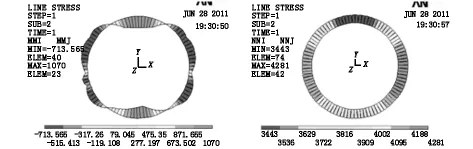
图12 接缝在拱顶两侧时结构内力图

图13 接缝在拱顶时结构内力图

根据上述工程实例的分析，可见无论采用梁弹簧模型计算还是修正惯用法计算，所得规律一致：考虑接缝构造影响后，当接缝布置在拱顶两侧时，拱顶处最大正弯矩减小，两侧最大负弯矩增大，正负弯矩比减小；当拱顶有接缝时，衬砌环的最大正弯矩反而增大。故利用接缝构造对内力影响的规律，通过变换接缝的位置可以调整最大正、负弯矩的峰值。

5 结论

a）盾构隧道接缝构造对结构内力的分布有一定的影响，可以利用该特点对结构设计进行优化，即尽可能使接缝处的混凝土接触面的形心位于管片厚度中心线内侧，且偏离距离越大，对弯矩的调整作用越大。同时管片拼装时应避免接缝位于正拱顶。

b）采用常用的修正惯用计算法或梁-弹簧模型进行盾构隧道结构内力分析时，宜根据具体的接缝构造设计方案对计算轴线进行适当调整，使计算结果更接近实际。

c）今后可以建立一种“通用”的接缝刚度试验方法，即对于某一给定厚度的管片，试验时可以将混凝土接触面的形心与管片厚度中心线重合，通过一系列的试验得出刚度与弯矩、轴力、接触面高度与管片厚度的比值三者之间的关系后，再用于理论计算，而接触面的偏心影响可以在计算模型中考虑。