T2 纯铜平板剪切试样的大变形破坏试验研究

李 柳，秦胜欢，熊再银，张克实

(广西大学 土木建筑工程学院，广西 南宁530004)

韧性材料在不同加载方式下的断裂应变有很大的不同，而现有的破坏理论以及用于材料强度和破坏分析的计算软件只适用于一些特殊应力状态的破坏准则，没能给出适用于不同应力状态下材料破坏的判据［1］。人们早已认识到应力状态对材料断裂应变有很大影响，并通过细观变形分析和轴对称试样破坏试验总结了拉伸加载下三轴应力状态影响断裂应变的原因［2-3］，但对于一般复杂加载条件下应力状态的影响，以及怎样估计相应状态下的材料断裂应变，仍有待于研究［4-5］。例如，能否利用材料的拉伸破坏试验预测剪切试验条件下的破坏应变?按现在常用的GTN 模型推测，韧性材料剪切断裂应变应远大于拉伸断裂应变，而从现有的试验数据来看，韧性材料的拉伸和剪切断裂应变的关系实际上没有明显的规律［1，5］。

剪切变形是连续介质的基本变形，剪切断裂应变是衡量材料抗破坏能力的重要参数。常见纯剪切试验可通过圆管试样扭转或平板剪切试样拉伸加载来实现，但实际上，韧性材料圆管扭转很容易进入屈曲而不再保持为纯剪切变形，不适合做纯剪破坏试验;实心圆棒做剪切破坏试验也会扭成麻花形状，使得试样横截面的变形和应力分布复杂而难以测定。一些学者认为平板剪切试样是比较可行的方案，通过单轴拉伸加载方式在试样韧带区域产生近似纯剪切变形并最后造成纯剪切破坏［4-9］。

常用描述应力状态的参数有应力三轴度Rσ和Lode 参数μσ。应力三轴度是指平均应力与等效应力的比值，它是影响材料中微孔洞演化的重要因素［10-12］。Lode 参数表示主应力之间的比值关系，它在加载过程中对空洞形状改变有重要影响［13］，而且在低应力三轴度下，材料的破坏与Lode 参数的关联度较高［14］。而在纯剪切或者近似纯剪切状态下，应力三轴度和Lode 参数等于零或接近于零。因此，采用剪切变形试样研究剪切破坏，必须对试样破坏区域的应力状态给出合理的估计。

由于所用纯铜材料具有较好的韧性，平板剪切试样韧带在变形过程中除强烈的剪切错动外还有很明显的转动。为探讨韧性材料应力状态与断裂应变的关系，本文对两种倾斜缺口根部几何不同的平板剪切试样进行破坏试验。采用数值模拟对试样断口倾角、韧带截面和断裂截面的应力三轴度、Lode 参数进行计算，并通过实测给出破坏区域的断裂应变估计。在此基础上，对平板剪切试样剪切断裂与光滑试样拉伸断裂进行比较分析。

1 试验分析

1.1 材料与试样

本文采用的T2 工业纯铜棒材的化学成分见表1。

材料先经600 ℃保温1 h 进行去应力高温退火处理，再线切割加工成试样，经湿磨抛光处理得到光滑表面。图1 给出两种平板剪切试样的几何轮廓，缺口韧带的宽度和厚度都是4 mm，韧带截面过中心且与纵向中心线平行。试样TS1 是圆弧形缺口，TS2 是尖角缺口。共用5 个TS1 试样和3 个TS2 试样进行了试验。

表1 工业纯铜T2 的化学成分Tab.1 Chemical composition 0f commercially pure copper-T2 wt%

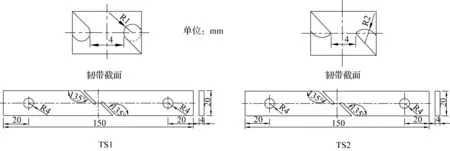
图1 平板剪切试样TS1 和TS2Fig.1 The plate shear specimen TS1 and TS2

1.2 试验方法

试验用MTS 拉扭疲劳试验机在室温条件下进行。为进行断裂应变比较，对光滑平板试样和光滑圆棒试样进行拉伸破坏试验。限于篇幅，本文只对剪切试验的试样和试验过程进行介绍。加载通过引伸计位移信号进行位移控制，引伸计标距段拉伸速度为0.5 mm/min。为了观察试样的破坏形式和裂纹萌生，将试样拉伸到单位面积载荷位移曲线进入急速下降后不同位置停止试验，用切割的方式把试样的纵向两端切下，留下中段20 ～30 mm 长的部分。再用线切割把中间部分对称切开，然后研磨抛光制成金相观察试样。于是可用超景深三维显微系统观察试样中裂纹萌生和扩展的状况。

1.3 试验结果与分析

首先考察试样的变形。变形前的试样和对应裂纹萌生时的试样如图2 所示(TS1 和TS2 试样变形规律相同，限于篇幅，只给出TS1 试样开始发现边缘裂纹萌生时的照片)。在轴向拉伸载荷下，两种试样都是在中间韧带区域承受相错的拉力造成的强烈剪切作用，该作用使得塑性变形不断增加，缺口宽度增大，缺口前缘靠试样中心一侧形状变尖锐并向前延伸，以及韧带区域逐渐沿顺时针方向转动。为估计韧带区域的变形，事先在试样过平面中心画上两条相互垂直相交的标记线，其一与试样纵向中心线(平行于拉伸轴)重合连接两个斜向缺口边缘，其二与横向中心线重合。可观察到试样标记线有以下变形过程:与纵向中心线重合的标记线始终保持为直线，但逐渐顺时针偏转，临断前转角达到约20°;而与横向中心线重合的标记线则从直线变为曲线，越接近试样中心曲率越大。这两条线的变形和转动反映了韧带区域的变形特点:横向标记线随变形弯曲表示该直线不同位置处剪切变形不同，弯曲越严重则剪切变形越大;纵向标记线保持为直线意味着沿该线各处剪切变形都近似相同。

其次，考察裂纹萌生及其以后的扩展。当载荷位移曲线开始急速下降时，可在试样缺口尖锐边缘(缺口靠近横向标记线一侧)发现萌生的裂纹，此时引伸计测得两种试样的伸长均约为37%。两种试样的裂纹都是沿着与拉伸轴呈接近45°的方向扩展(图3)，裂纹扩展速度很快，从启裂到韧带完全断裂的伸长很短。由试样上画的标记线(图2)可以看出，断裂的位置并不在之前的初始韧带截面(纵向标记线所在截面)位置。

图2 平板剪切试样TS1 的变形Fig.2 Deformation of plate shear specimen TS1

图3 平板试样TS1 的裂纹扩展Fig.3 Crack propagation of the plate specimen TS1

试验测得的试样单位面积载荷-位移曲线如图4 所示。两种试样的韧带横截面相同，由于缺口顶端几何形式不一样，测得的载荷-位移曲线有明显区别，如图4 所示。尖头缺口试样TS2 的缺口强化作用稍强一些，因为应力三轴度在尖头缺口前端要高于圆头缺口前端。TS2 试样最大载荷较TS1 试样大约高20%。而两种试样缺口前端应力三轴度的具体数值见后面的有限元分析结果。

2 试样剪切试验的数值模拟分析

2.1 材料参数

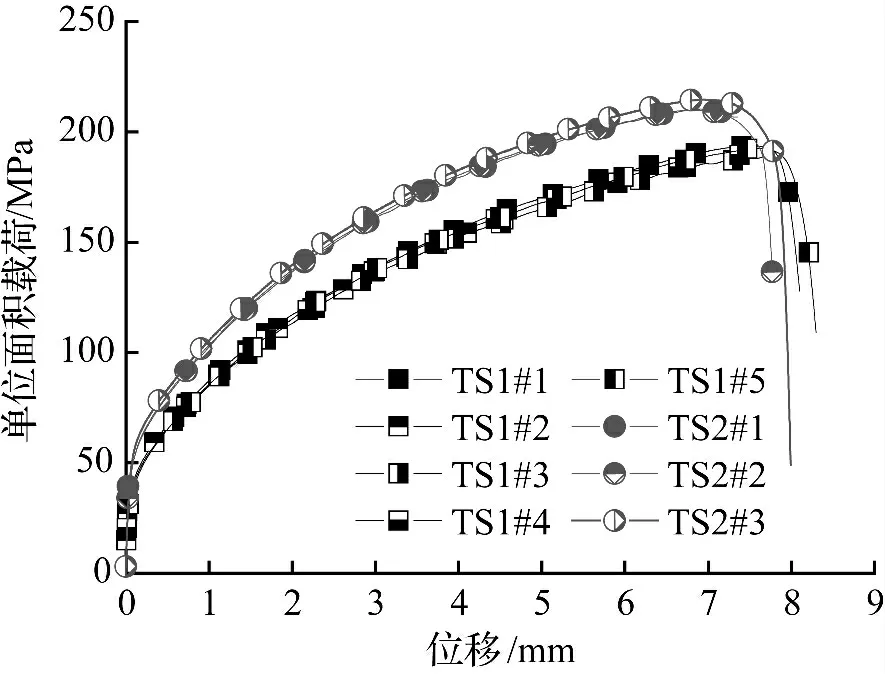
图4 试样的单位面积载荷－位移曲线Fig.4 Load elongation curves of specimens

T2 纯铜的弹性模量E=109.400 GPa，泊松比=0.328，通过纯铜光滑试件单轴拉伸试验得到材料的塑性参数，真应力-对数塑性应变曲线以及光滑试样试验和模拟的对比曲线如图5 所示。由图可见，数值模拟能精确地反映拉伸试验直到颈缩初始阶段的载荷位移曲线。

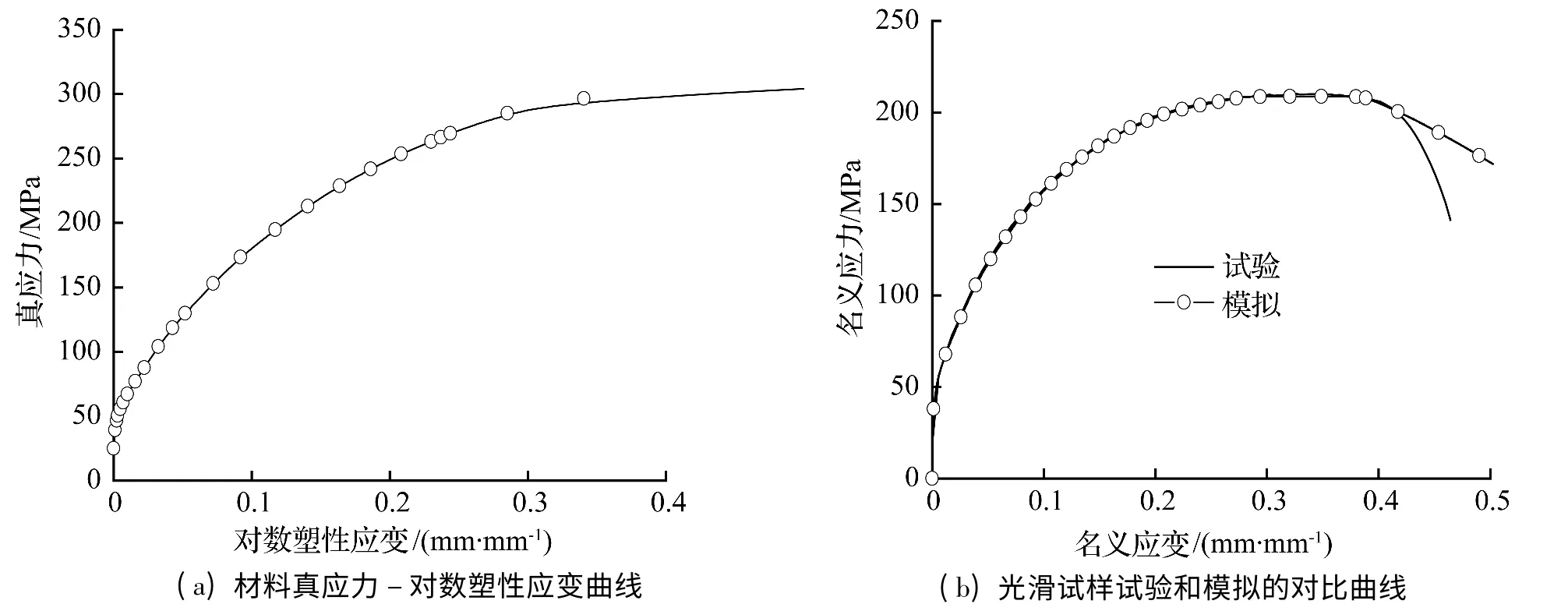
图5 材料真应力－对数塑性应变曲线以及光滑试样试验和模拟的对比曲线Fig.5 True stress-logarithmic plastic strain curveand nominal stress-strain curves by simulation and test

2.2 计算采用的单元和边界条件

采用有限元软件ABAQUS/standard 进行计算。有限元计算模型是按照图1 试样尺寸构建的，采用结构网格和C3D8 单元作单元划分，试样TS1 单元数是61 776，而TS2 单元数是57 824。由于是单调加载过程，计算采用等向强化模型，材料本构关系参数见“2.1 节”。数值模拟用位移控制加载，与试验一致。在模型两端各设置1 个参考点，参考点和试样端部通过耦合约束模拟试验机夹头对试样的夹持，一端固定而另一端加载。在试样中部相距25 mm 的位置设置两个节点，与实验引伸计触点一致。于是可通过历史变量输出模拟加载计算的试样引伸计标距段的伸长。

2.3 试样载荷-位移和变形的数值模拟

图6 给出数值模拟的TS1 和TS2 剪切试样的载荷-位移曲线。由图6 可以看出，数值模拟结果与实测在试样失稳之前吻合较好，而试样在失稳快速下降段，韧带的变形伴随着裂纹萌生和扩展，其过程十分复杂，因此，曲线进入快速下降的模拟结果误差增大。图7 给出TS1 模拟加载和试验实测的试样外廓变形图比较(图7(a)和图7(b))，可见，从大变形的试样外廓来看，数值模拟与实测很接近;从韧带区域的局部变形来看，模拟与实测的剧烈变形结果还是有差异。要改善模拟，需要对变形局部化过程的材料微结构和本构关系演化做进一步的研究。

2.4 韧带区域的应力状态

应力三轴度Rσ和Lode 参数μσ分别由以下公式定义

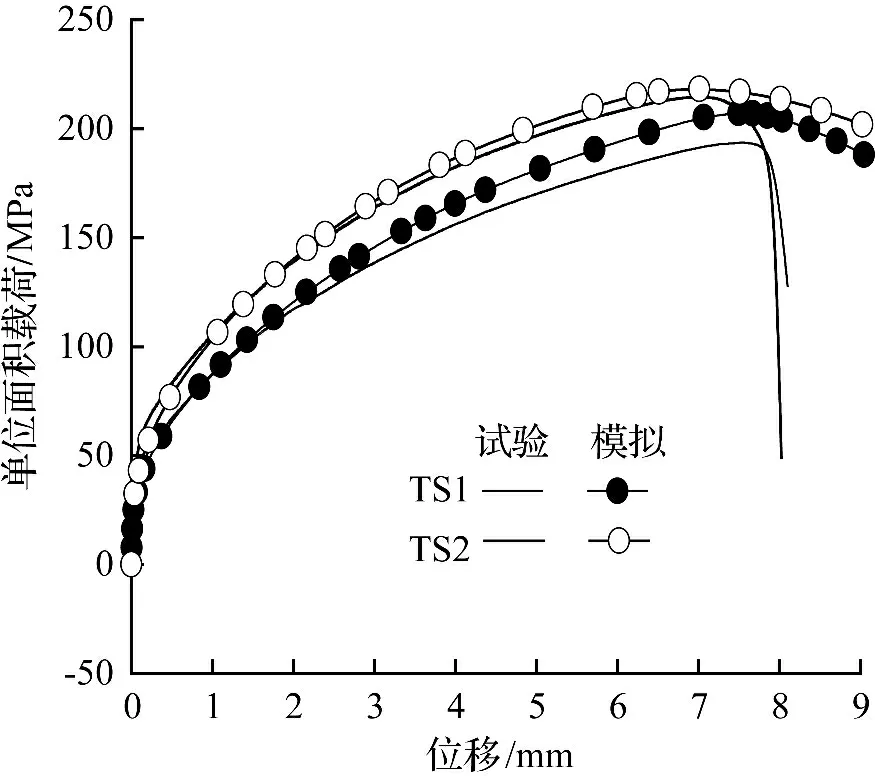
图6 TS1 和TS2 试样的试验与模拟对比曲线Fig.6 Comparisons of simulations and tests for TS1 and TS2 specimens

式中，σm为平均压力，σe为等效应力，σ1、σ2和σ3分别为第一主应力、第二主应力和第三主应力。应力三轴度Rσ和Lode 参数μσ都反映材料微元受力的三轴状态。对于Rσ，若等效应力不变，静水应力大意味着主应力的差异小，而材料塑性变形受到的约束增加。以往常用光滑和缺口拉伸试样的破坏试验来分析应力状态对断裂应变的影响，人们发现，对不同的缺口试样，Rσ值越大则断裂应变越小;光滑试样Rσ值相对很小而断裂应变相对很大［5，12，15］。对于μσ，它主要反映中间主应力与最大和最小主应力的比例，因此，主应力表征的单轴拉伸(μσ=-1)、纯剪切(μσ=0)到单轴压缩(μσ=1)以及不同的组合应力状态都可用μσ来描述。对于本文的试验，由于缺口几何的复杂性以及大变形造成的应力应变主方向的转动，需要对韧带及其破坏区域的应力状态进行计算分析。

图7 试样TS1 即将破坏时的计算变形和实测变形Fig.7 The calculated and tested deformations for specimen TS1 will be destroyed

前述断裂在缺口前缘靠近横向标记线一侧尖端启裂，沿与试样纵向近似45°角的方向扩展。由图7中用虚线绘出的示意试样断裂面可见，它与初始纵向标记线交角约25°，是实际断裂面;而纵向标记线所在剖面是设计试样时预估的破坏面，临断时该面已顺时针转动了约20°。预计断裂面和实际断裂面在试样表面和中面处的应力三轴度参数如图8 所示，Lode 参数如图9 所示，它们代表试样即将破坏时应力三轴度和Lode 参数在韧带所在面(预计断裂面)和实际断裂面的分布。由图8 和图9 可以看出，这两个面上应力三轴度都大于零，Lode 参数都小于零，即这些位置的应力状态是纯剪切与拉伸的迭加状态。

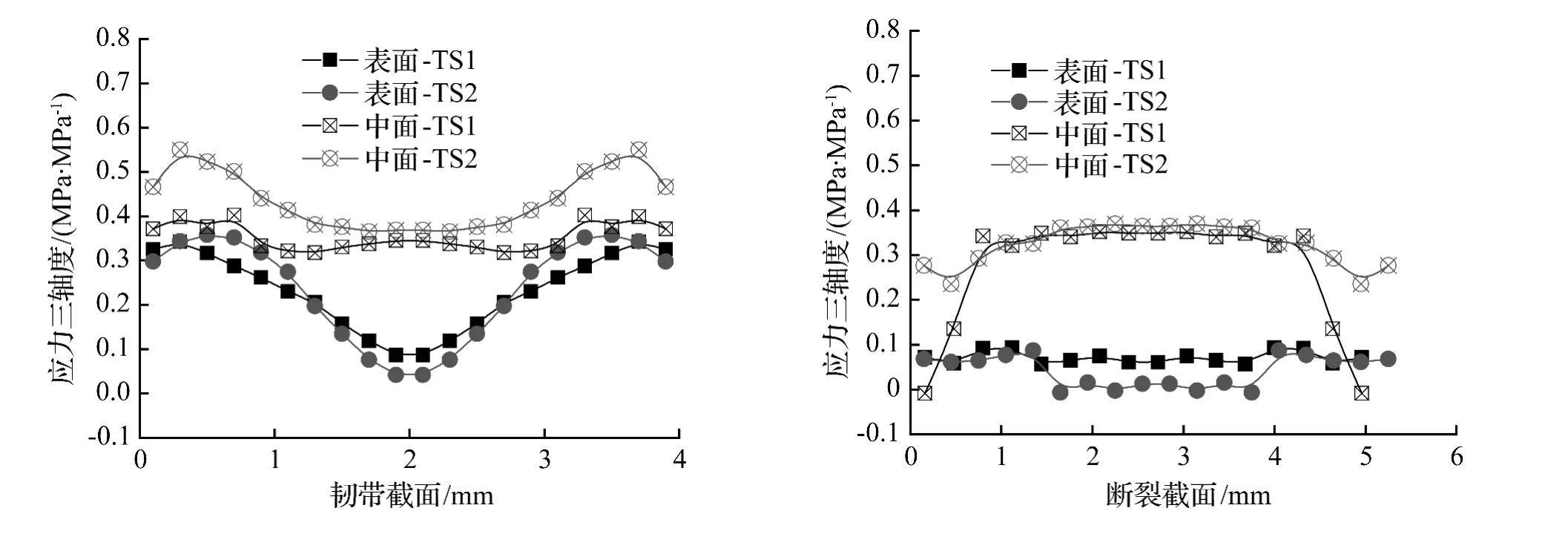
图8 应力三轴度在韧带截面和断裂截面上的分布Fig.8 Distribution of stress triaxiality across the ligament and fracture sections

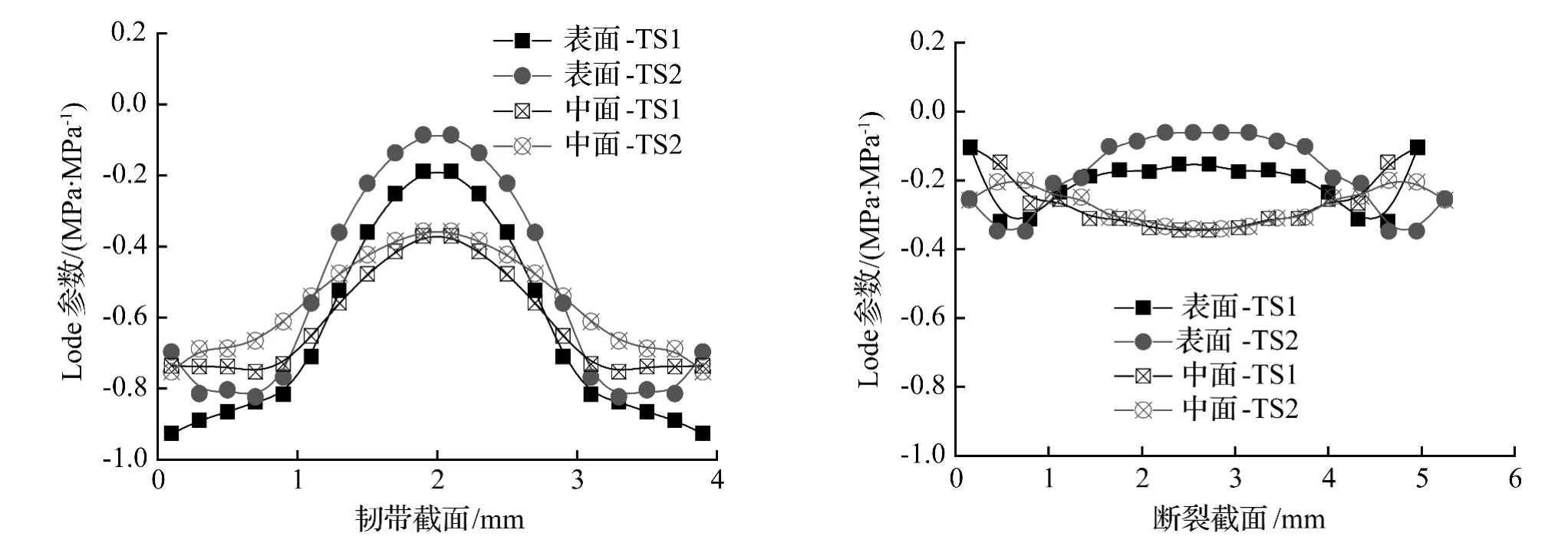
图9 Lode 参数在韧带截面和断裂截面上的分布Fig.9 Distribution of Lode parameters across the ligament and fracture sections

3 断裂应变估计与讨论

根据前述，试样在失稳快速下降段，韧带区域进入塑性变形局部化，模拟结果与实测差值迅速增大，韧带区域的剧烈变形难以通过有限元计算得到。而根据试样的标记线的变形，我们可以从图7(b)的局部放大图上观察到纵向标记线在横向标记线两侧的错动，并利用图7(c)的切变角γ(γ=0 对应初始状态)估计该区域的工程剪应变值，测得tgγ 约为4.33。对剪切主导区域，对数等效应变近似为εeq≈约为1.25。通过与表2 给出的平板和圆棒光滑拉伸试样测得的颈缩截面断裂应变进行比较可知，本文用T2 纯铜测得的剪切断裂应变与拉伸断裂应变接近(拉伸断裂应变在1.157 ～1.282)。

需要指出，圆棒光滑拉伸试样临断前试样心部(裂纹萌生点)应力三轴度Rσ接近1，若按Rice-Tracey 指数公式［10］，εf=αexp(-1.5Rσ)，则比较两种应力三轴度下材料断裂应变可按以下公式:

而前述剪切试验的分析表明，实际断裂面的应力三轴度在0 ～0.4(均值0.2)，而拉伸试样有颈缩现象，试样心部应力三轴度在0.6 ～0.8(均值0.7)。将应力三轴度均值代入式(3)进行估计，若采用Rice-Tracey 公式估计断裂应变，本文试样剪切断裂应变应该是光滑拉伸试样断裂应变的2 倍左右，该值远大于实测评估的断裂应变值。此例说明Rice-Tracey 公式不适用于剪切破坏估计。而Bao-Wierzbicki 提出的幂函数公式［1］，对于剪切试验，εf=aRσ2-bRσ+c(Rσ=0 ～0.4)，需要更多控制应力三轴度不同水平的试验来进行标定，其适用性有待进一步研究。

需要指出，Rice-Tracey 公式表述的断裂应变-应力三轴度的关系规律与其他模型，如得到广泛采用的GTN 模型是一致的，这些模型若用于剪切破坏分析也有类似问题。

表2 光滑试样的拉伸断裂应变Tab.2 The fracture strain of smooth specimen under tension

4 结 论

①纯铜平板剪切试样在单轴拉伸作用下，试样韧带截面有剧烈的剪切错动变形，且该截面在临断前约顺时针转动了20°，而断裂发生在与纵向加载方向约45°角方向，与韧带截面夹角约为25°，断口接近于平面。

②平板剪切试样韧带附近区域，从载荷作用开始直至破坏是以剪切为主的混合应力状态。

③T2 纯铜平板剪切试样的断裂应变与拉伸试样的断裂应变近似相等，与Rice-Tracey 指数公式描述的规律不符。

［1］ BAO Y，WIERZBICKI T.On fracture locus in the equivalent strain and stress triaxialityspace［J］.International Journal of Mechanical Sciences，2004，46(1):81-98.

［2］ MCCLINTOCK F A.A criterion of ductile fracture by the growth of holes［J］.Journal of Applied Mechanics，1968，35:363-71.

［3］ HANCOCK J W，MACKENZIE A C.On the mechanisms of ductile failure in high-strength steels subjected to multi-axial stress-states［J］.Journal of the Mechanics and Physics of Solids，1976，24:147-69.

［4］ BJÖRKLUND O，NILSSON L.Failure characteristics of a dual-phase steel sheet［J］.Journal of Materials Processing Technology，2014，214(6):1190-1204.

［5］ LI H，FU M W，LU J，et al.Ductile fracture:experiments and computations［J］.International Journal of Plasticity，2011，27(2):147-180.

［6］ GAO F，GUI L，FAN Z.Experimental and numerical analysis of an in-plane shear specimen designed for ductile fracture studies［J］.Experimental Mechanics，2011，51(6):891-901.

［7］ TARIGOPULA V，HOPPERSTAD O S，LANGSETH M，et al.A study of large plastic deformations in dual phase steel using digital image correlation and FE analysis［J］.Experimental Mechanics，2008，48(2):181-196.

［8］ 高付海，桂良进，范子杰.两种新型单拉平板剪切试件的设计与对比［J］.清华大学学报:自然科学版，2010，50(2):299-302.

［9］ 朱浩，齐芳娟，张洋.剪应力状态下6061 铝合金的力学性能及断裂行为［J］.中国有色金属学报，2012，22(6):1570-1576.

［10］RICE J R，TRACEY D M.On the ductile enlargement of voids in triaxial stress fields［J］.Journal of the Mechanics and Physics of Solids，1969，17(3):201-217.

［11］BAO Y.Dependence of ductile crack formation in tensile tests on stress triaxiality，stress and strain ratios［J］.Engineering Fracture Mechanics，2005，72(4):505-522.

［12］郑长卿，周利，张克实.金属韧性破坏的细观力学及其应用研究［M］.北京:国防工业出版社，1995.

［13］ZHANG K S，BAI J B，FRANCOIS D.Numerical analysis of the influence of the Lode parameter on void growth［J］.International Journal of Solids and Structures，2001，38(32):5847-5856.

［14］DANAS K，CASTANEDA P P.Influence of the Lode parameter and the stress triaxiality on the failure of elasto-plastic porous materials［J］.International Journal of Solids and Structures，2012，49(11):1325-1342.

［15］张丽敏，张克实，石艳柯.纯铝缺口试样厚度与缺口深度对拉伸破坏的影响［J］，广西大学学报:自然科学版，2009，34(4):438-443.