FV520B不锈钢铣削稳定叶瓣图的构建及实验*

李宏坤，赵鹏仕，李精忠，董 雷（大连理工大学机械工程学院 大连，116023）

FV520B不锈钢铣削稳定叶瓣图的构建及实验*

李宏坤，赵鹏仕，李精忠，董 雷
（大连理工大学机械工程学院 大连，116023）

为了提高压缩机叶轮的加工效率，研究了解析法构建铣削稳定性叶瓣图的方法，并利用该方法实现对FV520B材料加工的参数优化。通过该方法可以选取合适的加工转数和切削深度，避免颤振，使加工后的工件达到要求的精度及表面质量，并能够保护刀具和机床的安全、可靠度。通过实验数据分析，获取构建叶瓣图的所需参数，构建稳定性叶瓣图，并在所构建的叶瓣图中选取不同测试点，对叶瓣图进行正确性验证。研究表明，该方法在实际叶轮加工制造中具有重要意义。

铣削颤振；稳定域；模态分析；FV520B

1 问题的引出

由于叶轮材料的难加工特性，使得加工制造高精度、高质量的叶轮成为难题，因此在铣削加工过程中选取合适的切削参数对于提高加工精度及质量具有重大意义。叶轮机械中叶轮是重要的核心工作件，由于要承载工作载荷并适应其较恶劣的工作环境（高温高压），故叶轮的材料选择条件较为苛刻。FV520B钢材经过热处理后，可以达到1 100～1 300 MPa的耐压强度，对大气及稀释酸或盐都具有良好的抗腐蚀能力。这种材料已经广泛用于叶轮制造、航天工业及其他军事工业。图1为FV520B在五轴加工中心进行叶轮加工。

图1 五轴加工中心加工叶轮Fig.1 Five-axis center milling impeller

FV520B虽然可以满足叶轮的要求，但存在难加工的问题。高强度、硬度使得切削过程中切削力大；切削区局部温度高，刀具易磨损；韧性和塑性较高，切屑不易折断分离；它和其他材料亲和性强，易产生粘附现象。必须选择良好的切削参数才能使加工表面达到精度及质量要求。

在切削加工叶轮的时候会因为刀具悬伸量大、精度要求高等因素引发切削颤振，而避免颤振发生最有效的方法是使用颤振稳定性叶瓣图。文献［1］建立了基于切削厚度再生效应的动态铣削了模型，首先提出了零阶解析法（zero-order analytical，简称ZOA）。刘强等［2］采用ZOA方法获得了车削及铣削过程，平头刀、球头刀和R刀的稳定性叶瓣图，讨论了切削参数和模态参数等对稳定性叶瓣图的影响。

笔者对FV520B的颤振稳定域分析进行研究，以获取最佳的转速，提高切削效率。对动力学模型的优化进行了分析，在构建叶瓣图后对其进行实验验证，为FV520B加工效率的提高提供技术支撑。

2 稳定性叶瓣图的构建原理

铣削系统可以简化为二自由度系统，如图2所示。铣削过程动力学方程［3］可以表示为

其中，mx，my，cx，cy，kx，ky分别为x，y方向上机床-刀具系统的质量、阻尼和刚度；Fxj和Fyj分别为作用在铣刀刀齿j上的切削力在x和y方向上的分量。

图2 二自由度铣削系统Fig.2 Two-degree of freedom milling system

在铣削加工中，只考虑再生颤振的动态切削厚度表达式为

基于Tlusty［4］提出正交切削理论的模型当瞬时角位移为时，作用在刀齿j上的切向和径向动态切削力可以表示为

其中：Kr为系数比，Kr=Krc/Ktc。

将式（2）代入式（3），对各方向上的力求和得到

其中：axx，axy，ayx，ayy为方向系数式。

式（4）可以改写成矩阵的形式

其中：A（t）为与瞬时角位移φj相关的周期函数；其角频率ω=Nn/60；周期T=2π/ω。

对A（t）进行Fourier级数展开并保留第1项，

则式（5）改写为

其中：axx，axy，ayx，ayy为平均方向系数。

通过对式（1）进行整理并进行拉氏变换，其传递函数［3］可表示为

其中：ζx，ζy为阻尼比；ωnx，ωny为系统固有频率。

系统稳定的充要条件是传递函数G（s）特征方程的根均具有负的实部。频域中切削力可以表示为

其中：ωc为颤振频率［5］。

铣削再生颤振频率下的闭环反馈系统的特征方程为

Λ为方程的特征值，其表达式［6］为

其中：a0=Gxx（iωc）Gyy（iωc）（αxxαyy-αxyαyx）；a1=αxxGxx（ iωc）+αyyGyy（iωc）。

由于G（iωc）中存在虚数，而切深为实数，故令Λ =ΛR+iΛI，e-iωct=cosωcT-isinωcT，代入式（10）并令虚部等于零，得

其特征值解析法表示为

由式（12）和式（10）得到临界轴向切深［6］为

其中：k为叶瓣图中的叶瓣数。

从式（13），（14）可知，对于一个给定的机床-刀具-工件系统，只要知道颤振频率（系统固有频率附近）、铣刀齿数、刀具切削系数和切削系统频率响应函数，就能够计算出轴向临界切深和相对应的主轴转速，进而可以构建出颤振稳定性叶瓣图［7］。

由式（12）得到主轴转速为

3 实验数据采集及分析

3.1 模态实验

模态实验是通过振动测试来确定系统的固有频率、阻尼比、刚度和模态振型，是一种用来分析机构动力学特性的方法。模态实验在大连理工大学模具所东昱精机CMV-850A加工中心上进行。实验用刀具为英国斯特拉姆（ATI Stellram）公司生产的7792VXD型牛鼻铣刀（刀片型号为ATI stellram-X500，基质为硬质合金），刀具直径为32 mm，悬伸长为200 mm，刀片数为3个。模态实验设备包括：冲击力锤；加速度传感器，灵敏度为93 m V/g；NI USB-9234型4通道数据采集卡；北京东方振动与噪声技术研究所Coinv DASP V10多通道信号采集和实时分析软件。图3为模态实验的测试装置示意图。

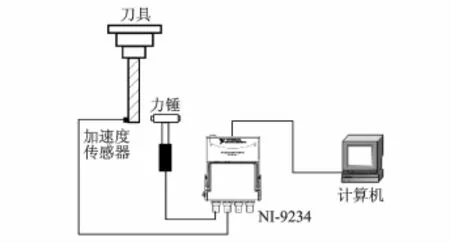
图3 模态实验的测试装置示意图Fig.3 Modal experiment test device schematic

采样参数设置：采样频率为5 120 Hz，采样点数为54 576。为了提高模态测试精度，采用三次锤击激励然后求取平均值。图4为x，y方向的刀具频率响应曲线。

图4 x，y方向刀具频响函数曲线Fig.4 x，y direction frequency response function curve of tool

通过DASP模态分析软件提供的Poly LSCF算法，这是一种采用离散时间频域模型的方法，通过选取合适的阶数和总体拟合，达到所需精度。Poly LSCF算法对于第1阶模态具有特别高的精度，抗干扰能力强，稳态图清晰，并且易于区分虚假模态，运算速度快。由于后n阶模态最后的处理方法相同，影响因子小，并且在最后处理中所得到的稳定性叶瓣图也是取曲线下稳定区域的交集，这里仅以第1阶模态的计算做分析处理。刀具的x，y方向的模态参数如表1所示。

表1 刀具模态参数Tab.1 modal parameters of tool

3.2 铣削力实验

铣削力系数辨识实验在大连理工大学模具所东昱精机CMV-850A加工中心上进行，材料为FV520B钢，刀具型号与模态实验相同，测力仪为大连理工大学传感测控研究所YDX-III97型三向铣削力测试平台，采样频率为20 k Hz。图5为铣削力测量装置示意图。

图5 铣削力测量装置示意图Fig.5 Milling force measuring devices schematic

切削实验考虑三因素（主轴转速n、切深ap和进给速度f），每个因素3个水平方向按正交表L9（33）设计实验。正交实验具有均匀分散、整齐可比的特点，通过交互安排影响实验因素的参数进行实验，达到高质量、高精度的实验结果，并可以有效节省实验的人力、物力和财力［8］。3个因素初步认为影响因子相同，确定的切削参数见表2。

表2 切削参数Tab.2 Milling parameters

通过Matlab编程计算，将切削力在x，y，z 3个方向上计算平均铣削力大小，其平均切削力测试结果如表3所示。

通过切削力系数计算理论及回归分析，可以计算出6个铣削力系数［9］。铣削力系数如表4所示。

表3 实验测量平均铣削力Tab.3 Average force from experiment measuring

表4 切削系数Tab.4 Milling coefficient

4 构建叶瓣图及验证

4.1 叶瓣图的构建

利用模态分析所得数据进行Matlab编程，绘制FV520B钢材的稳定性叶瓣图如图6所示。从图6中可以看出，选择曲线下方的切削参数进行加工为稳定加工区域，其中选择虚线以下部分的切削参数为绝对稳定区，选择曲线以上部分的切削参数进行切削为容易发生颤振的颤振区域。根据叶瓣图选取合理的加工参数可以避免颤振，获得比较高的加工效率、良好的加工表面及精度，并且保护机床与刀具。图6中在主轴转速500～1 500 r/min之间有较大的稳定区域，在制定切削参数时优先选在该区域选取，并尽量避免靠近叶瓣图曲线。

图6 FV520B钢铣削稳定性叶瓣图Fig.6 Milling stability lobes of FV520B

4.2 稳定性叶瓣图的验证

选择A，B两点不同的切削参数进行验证，图7中，A处在叶瓣图的稳定区域，B处在叶瓣图的颤振区域，C点处在稳定区域。其中：A，B，C三点的切削参数如表5所示。

图7 叶瓣图中验证点的选取Fig.7 Verification points selection from lobes

表5 验证实验切削参数Tab.5 Verification experiment milling parameters

稳定性的验证可以通过分析处理力信号来检测，也可以通过观察所加工表面的精度及质量来区分。表面质量及精度没有国家标准来区分是否发生颤振，而是通过所采集的力信号的分析处理。采用快速傅里叶变换观察其时域信号及频域信号的特征，很容易判断是否发生颤振［10］。A点力信号数据如图8所示。A点的时域信号平稳可靠；频域信号中，由于刀齿数N=3，转数为800 r/min，对应主轴转频为13.3 Hz，切削频率为39.8 Hz（13.3 Hz× 3）。振动幅值最大的对应频率为转频和切削频率，没有出现颤振相关频率。B点力信号数据如图9所示。B点的时域信号不好做判断；在频域信号中，其主轴转速为1 000 r/min，对应主轴转频为16.6 Hz，切削频率为49.8 Hz（16.6 Hz×3）。频谱图中幅值最大的频率为268.6 Hz，与切削系统的固有频率接近。颤振发生时，颤振频率在切削系统固有频率附近，故选择在B点切削参数进行切削，已发生颤振。

C点力信号数据和A点类似，没有出现颤振相关频率，铣削过程是稳定切削，与预判断的结果一致。证明了笔者所构建的铣削稳定性叶瓣图正确可靠。

图8 A点的铣削力信号分析（800 r/min，0.5 mm）Fig.8 Cutting force analysis at A（800 r/min，0.5 mm）

图9 B点铣削力信号分析（1 000 r/min，0.5 mm）Fig.9 Cutting force analysis at B（1 000 r/min，0.5 mm）

5 结束语

通过解析法构件加工稳定性叶瓣图，对难加工叶轮材料FV520B的实际切削优化了切削参数，使切削颤振现象得到了控制。这也验证了该方法的正确性和可靠性，提高了加工精度、效率和表面质量，保护了刀具及机床的安全。可见，ZOA解析法构建叶瓣图可以避开颤振区域，简洁方便，可靠性好，可以推广应用于其他材料工件的实际加工应用当中。

［1］ Budak A Y.Analytical prediction of stability lobes in milling［J］.CIRP Annals-Manufacturing Technology，1995，44（1）：357-362.

［2］ 刘强，李忠群.数控铣削加工过程仿真与优化-建模、算法与工程应用［M］.北京：航空工业出版社，2011：70-90.

［3］ 丁烨.铣削动力学-稳定性分析方法与应用［D］.上海：上海交通大学，2011.

［4］ Tlusty J，Ismail F.Basic non-linearity in machining chatter［J］.CIRP Ann-Manufacture Technology，1981，30：299-304.

［5］ 李忠群.复杂切削条件高速铣削加工动力学建模、仿真与切削参数优化研究［D］.北京：北京航空航天大学，2008.

［6］ Budak E，Altintas Y.Analytical prediction of chatter stability in milling.part 1：general formulation［J］.Proceedings of the ASME，Dynamics System and Control Division，1995，57（1）：545-556.

［7］ Altintas Y，Ko J H.Chatter stability of plunge milling ［J］.CIRP Annals，2006，55（1）：361-364.

［8］ Xu Zhongan，Wang Tianbao.Brief introduction to the orthogonal test design［J］.Science/Tech Information Development＆amp；Economy，2002，12（5）：148-150.

［9］ Minis I，Yanushevsky T.A new theoretical approach for the prediction of machine tool chatter in milling ［J］.Journal of Engineering for Industry，1993，115：l-8.

［10］吴石，刘献礼，王艳鑫.基于连续小波和多类球支持向量机的颤振预报［J］.振动、测试与诊断，2012，32（1）：46-50.Wu Shi，Liu Xianli，Wang Yanxin.Chatter prediction based on continuous wavelet features and multi-class spherical support vector machine［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2012，32（1）：46-50.（in Chinese）

TG502.14；TH17

10.16450/j.cnki.issn.1004-6801.2015.04.020

李宏坤，男，1974年9月生，教授。主要研究方向为颤振稳定域分析、动态系统测控和故障诊断。曾发表《基于KPCA-SCM的柴油机状态识别研究》（《振动、测试与诊断》2009年第29卷第1期）等论文。

E-mail：lihk@dlut.edu.cn

*辽宁省科技创新重大专项基金资助项目（201303002）

2013-07-30；

2013-10-09