基于混台验前分布的复杂装备测试性评估*

张西山，黄考利，闫鹏程，连光耀，王韶光（.军械工程学院四系 石家庄，050003）（.军械技术研究所一室 石家庄，050003）

基于混台验前分布的复杂装备测试性评估*

张西山1，黄考利2，闫鹏程2，连光耀2，王韶光2
（1.军械工程学院四系 石家庄，050003）（2.军械技术研究所一室 石家庄，050003）

合理有效地利用验前信息是小子样评估中的关键问题。针对复杂装备小子样测试性评估问题，考虑了不同验前信息的可信度和重要度，提出了一种混合Beta分布的复杂装备小子样测试性评估方法。算例表明，在小子样前提下，传统统计方法得到的测试性置信下限过于保守；现有的可信度度量方法大都直接基于数据层，没有考虑验前信息的来源。混合Beta分布的复杂装备小子样测试性评估方法不仅考虑了验前信息的可信度，还对验前信息的重要度进行了分析，评估结论更加合理，具有较好的工程应用价值。

测试性评估；小子样；可信度；重要度；混合Beta分布

引 言

复杂装备系统由于造价昂贵，测试性评估不可能通过大量的现场试验进行，导致试验数据的缺乏。运用传统的评估方法很难得到理想结果。小子样分析评估技术已经在多个领域得到应用［1-3］。在小子样测试性评估中，有大量的专家经验信息、子系统试验信息和虚拟仿真试验信息等可以利用。这些信息的采用弥补了现场试验信息的不足，可以在不降低置信度的前提下减少试验次数，节省试验产品，缩短试验周期［4］。这些验前信息是在不同的试验条件下获得的，如何利用这些多源验前信息给出验前分布，即多源验前信息的融合是Bayes小子样测试性评估中函需解决的问题［5］。在验前信息的融合中，目前的融合方法主要是基于分布加权的验前信息融合。文献［6］提出了基于可信度的动量轮Bayes可靠性评估，从验前信息嫡的角度提出了一种可信度概念，利用不同验前信息的可信度来定量刻画信息间的差异。文献［7］研究了利用专家信息进行验前分布融合的方法。文献［8］考虑了Bayes可靠性评估中产品的继承性，将继承因子引入到验前信息的融合中。先验信息可信度的Bayes评估方法只考虑了数据本身，没有考虑数据来源，是以统计学知识为基础，具有一定的采伪或者错判的概率。利用专家信息获得权重因子主观性较强，从而导致可信度不高。对于基于继承因子的多源信息融合方法，在没有相似产品或改动较大的全新装备上的应用受到一定的限制。

笔者建立了一种基于多源验前信息融合的小子样复杂装备系统测试性分析评估模型。首先，确定了不同验前信息对应的验前分布；然后，根据验前信息可信度和重要度融合这些验前分布为混合验前分布；最后，利用现场试验数据推断验后分布进行测试性评估。

1 验前信息获取

1.1 验前信息分类

对于复杂装备系统来说，在装备投入使用之前，存在大量的子系统试验信息、专家经验信息和虚拟仿真信息可供利用［8-9］。

1）子系统试验信息。在研制阶段，装备整体的测试性试验信息较少，子系统试验信息相对较多，可将子系统试验信息折合为装备系统测试性信息，得到系统测试性验前值。

2）专家经验信息。工程专家通过长期的现场工作实践积累下来的经验知识是十分重要的验前信息。

3）虚拟仿真信息。通过建立测试性仿真模型，利用计算机对较复杂的现象进行仿真。仿真的方法是获取验前信息的重要途径。

1.2 验前分布形式

对于服从二项分布的测试性成败型试验总体，工程应用中常用Beta（α，β）分布作为其验前分布，设故障检测率（fault detection rate，简称FDR）为P，n种来源的验前信息各自对应的验前分布为

其中：αi，βi为验前分布参数，分别表示历史试验的成功数和失败数。

在验前分布形式已知的情况下，确定αi，βi的值是确定验前分布的关键。

故障检测率P的均值和方差为

2 验前分布参数确定

2.1 基于子系统试验信息的验前分布参数确定

设第i个分系统的故障检测率为Pi，则验前分布为Beta（Pi；αi，βi），结合子系统少量的成败型试验数据（ni，fi），利用Bayes公式计算得Pi的后验分布为Beta（Pi；αi+ni-fi，βi+fi），求得Pi的一阶矩E（Pi）和二阶矩E（P2i）分别为

设综合后相当于系统进行了N次现场试验，F次失效，对于由m个子系统串联起来的系统，故障检测率P=∏mi=1Pi，则

两式联立可求得N，F，α=N-F，β=F。

2.2 基于专家经验信息的验前分布参数确定

设共有n位专家，一共给出n个连续区间［Pi，L，Pi，H］，i=1，2，…，n，专家权重为ωi。基于经典概率统计理论综合各位专家信息后的系统P均值和方差为

联合式（2），（3），（8），（9），得到αi，βi的值。

2.3 基于虚拟仿真信息的验前分布参数确定

假设虚拟仿真试验数据X=（X1，X2，…，Xi，…，Xn）经过一致性检验。ωi为第i批仿真试验数据经过证据理论合成规则得到的权重；mj为第j批虚拟仿真试验的故障样本总数；sj为故障检测成功样本总数。第j批虚拟仿真试验的故障检测率为

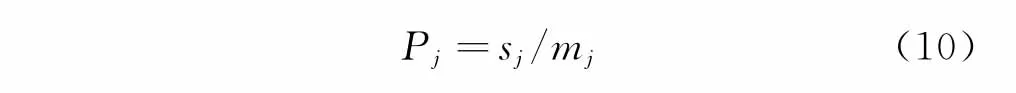
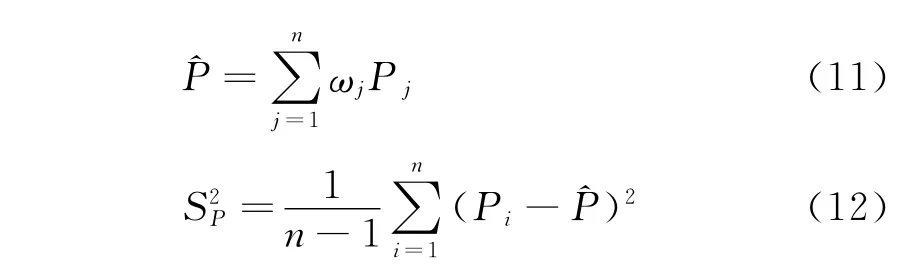
系统故障检测率的验前估计值和方差为联合式（2），（3），（10）～（12），求得αi，βi的值。

3 复杂装备系统测试性评估模型

3.1 融合多源验前信息的混合验前分布

由于测试性试验条件等客观因素的存在，其现场试验样本与历史试验样本一般来说来自不同总体。为了有效利用验前信息，描述验前信息与现场信息的异总体性，并减少历史试验样本与现场试验样本异总体性对测试性评估的影响，需要以某种恰当的形式对历史试验信息进行融合［10］。

目前，对多源信息进行加权融合的方法通常有两种：a.考虑验前信息可信度的多源验前信息融合［11］；b.专家信息确定验前分布的权重［12］。基于可信度的验前信息融合是以统计学知识为基础的，具有一定的采伪或者错判的概率。因此对于验前分布的融合不仅要考虑验前信息的可信度，还要考虑信息本身的来源，对验前信息的重要度进行分析。下面以验前信息的可信度和重要度为基础，给出验前信息融合的混合加权模型。

记有不同来源的验前分布分别为πi（P），各验前信息的可信度为ci，重要度为ωi，i=1，2，…，n。融合后的验前分布为

3.2 可信度c的确定

设从实物试验获得参数θ的概率密度为g（θ），从验前信息获得参数θ的验前概率密度为π（θ），两种信息概率密度的重叠大小可以反映两种信息的相似程度。两者的重叠区域越大，则验前信息包含的有效信息越多，即可信度越高；反之，可信度越小，如图1所示。

图1 可信度计算示意图Fig.1 The calculation diagram of credibility

直接由验前密度函数π（θ）和实物试验概率密度函数g（θ）的重合程度来直观定义仿真数据的可信度［13］，定义为

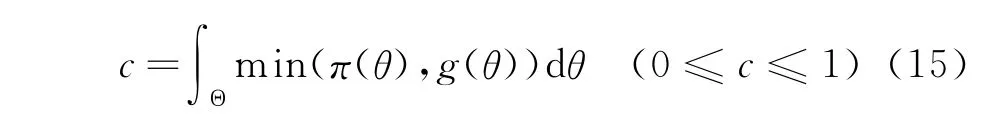
3.3 重要度ω的确定

假设在现场试验之前，由m个不同数据来源的验前分布πi（θ）（i=1，2，…，m）。应用层次分析法确定各信息源的重要度，具体步骤［7］如下。

1）运用专家打分等方法构造各信息源重要度的比较矩阵Bm×m

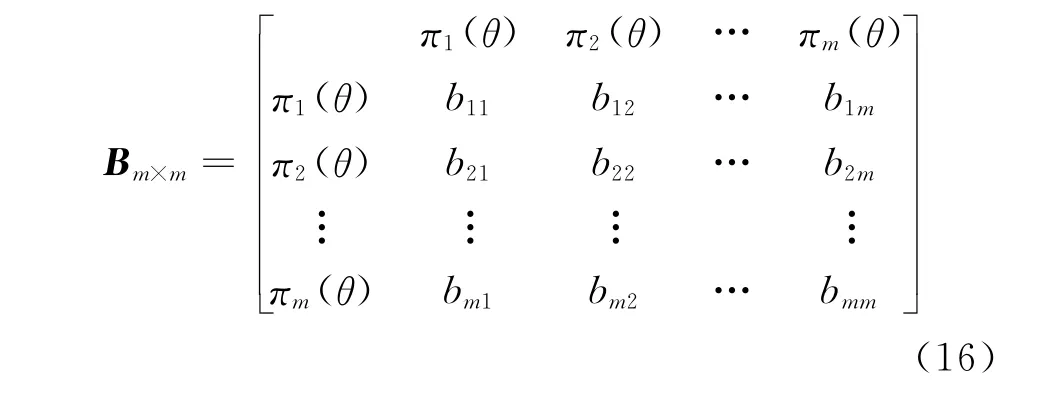
2）将比较矩阵每一列正规化

3）每一列正规化后的矩阵按行相加

5）得出的向量ω=（ω1，ω2，…，ωm）T即为各信息源的相对重要度。

3.4 验后分布确定

假设现场试验获得的成败型样本为X（n，f），依据Bayes定理，代入现场试验样本，整理得到验后分布π（P|X）为

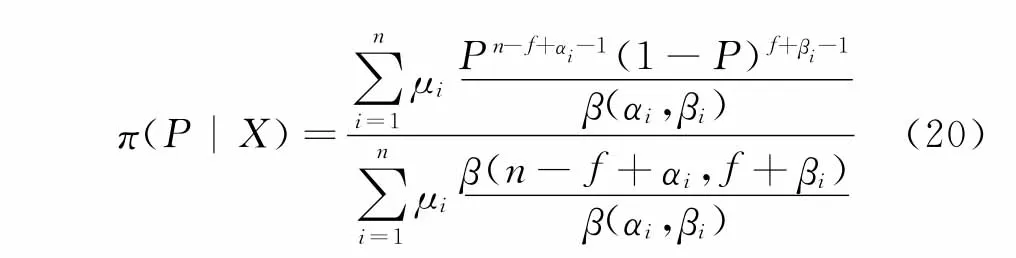
4）对向量W=（W1，W2，…，Wm）T正规化

将π（P|X）代入，求出装备系统在给定置信度γ下的置信下限PL和故障检测率P的各阶矩为

4 实例分析

图2 某型装备结构框图Fig.2 The structure diagram of some equipment

某武器装备由4个分系统串联组成，如图2所示。该装备系统在设计、研制过程中进行了大量的分系统试验，分系统试验数据及超参数计算结果如表1所示。根据表1的试验数据，代入式（4）～（7），计算出α=53.36，β=3.92，即由分系统计算得到的验前分布为π1（P）=Beta（53.36，3.92）。

通过建立测试性验证虚拟样机，利用蒙特卡洛方法生成故障样本集，在虚拟样机上进行故障注入，启动BIT仿真模型进行虚拟测试。得到的虚拟仿真试验数据结果如表2所示，权重由证据合成规则得到。

根据表2的试验数据，代入式（2），（3），（10）～（12），计算得到α=49.86，β=4.97，即由虚拟仿真试验数据计算得到的验前分布为π2（P）= Beta（49.86，4.97）。进行了28次现场试验，失败1次，即n=28，f=1。对此型武器装备进行测试性评估，置信度γ取为0.9。

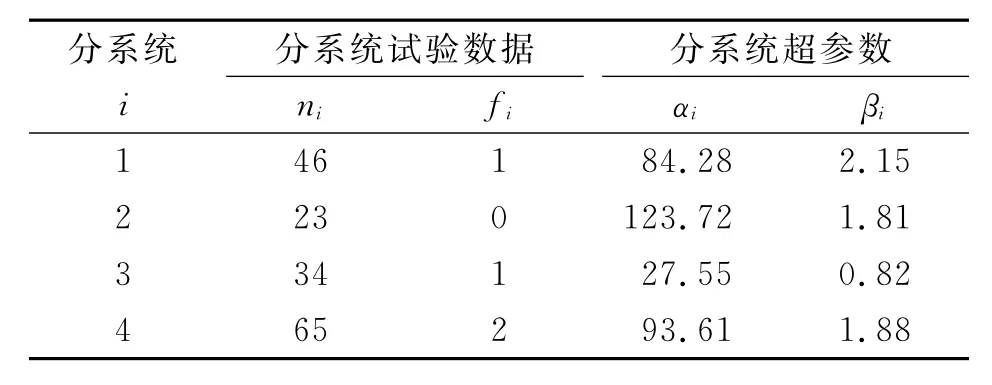
表1 分系统试验数据及超参数Tab.1 FDR experiment information of certain equipment subsystem

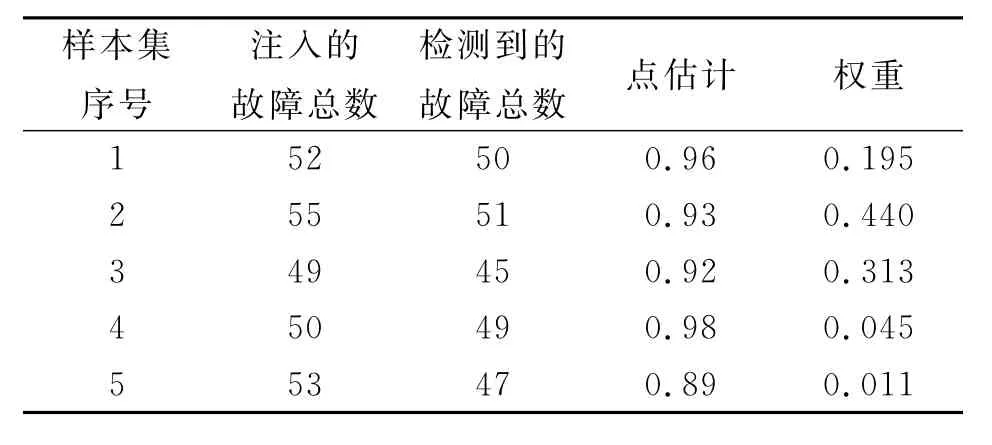
表2 虚拟仿真试验数据Tab.2 FDR virtual simulation experiment information

图3 3种试验FDR的概率密度Fig.3 The probability density function of three test

测试性试验时，对装备实施故障检测和故障离程序并作出故障指示，结果只有成功或失败两种形式。每次试验独立进行，测试性试验可看作是成败型试验，以二项式分布为基础进行评定。本例中若采用经典统计方法，则

其中：PL为P的置信下限；取置信水平γ=0.9；将现场试验数据代入得到故障检测率置信下限PL= 0.868 1。

若只采用可信度进行验前信息加权融合，忽略验前信息来源的重要度，得到故障检测率置信下限PL=0.965 8。通过对比发现，采用本研究方法计算得到的结果大于直接采用现场试验数据计算得到的结果，而小于只采用可信度进行验前信息加权融合得到的结果，这样就避免了仅利用现场数据方法的“保守”与直接只采用可信度进行验前信息加权融合方法的“冒进”。

5 结束语

利用分系统试验数据和虚拟仿真试验数据，并结合现场试验信息，以一种新的Beta分布作为验前分布，通过Bayes数据融合的方法，对某型装备系统的故障检测率进行了分析。该方法考虑了不同验前信息的可信度和重要度，较为合理地利用了各种验前信息，简便易行，在工程研究领域具有很好的实用价值。

［1］ 杨华波，蔡洪，张士峰.基于混合验前分布的制导精度评定方法［J］.航空学报，2009，30（5）：855-860.Yang Huabo，Cai Hong，Zhang Shifeng.Evaluation of missile guidance precision based on hybrid prior distribution［J］.Acta Aeronautica et Astronautica Sinica，2009，30（5）：855-860.（in Chinese）

［2］ 陈宏志，芦永明，王丽娜，等.较小样本动态声发射信号多元统计分析技术［J］.振动、测试与诊断，2013，33（2）：199-203.Chen Hongzhi，Lu Yongming，Wang Lina，et al.A-nalysis of dynamic acoustic emission signals using multivariate statistical technique for smaller dataset［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2013，33（2）：199-203.（in Chinese）

［3］ Wu Jianing，Yan Shaoze，Xie Liyang，et al.Reliability apportionment approach for spacecraft solar array using fuzzy reasoning Petri net and fuzzy comprehensive evaluation［J］.Acta Astronautica，2012，76：136-144.

［4］ 雷军华，秦开宇.确定测试性验证试验方案的贝叶斯方法［J］.系统工程与电子技术，2012，34（12）：2612-2616.Lei Huajun，Qin Kaiyu.Bayesian method for determination of testability demonstration test scheme［J］.Systems Engineering and Electronics，2012，34（12）：2612-2616.（in Chinese）

［5］ 吴建业，周海银.基于混合先验分布的导弹武器系统飞行可靠性评估［J］.飞行器测控学报，2008，27（1）：26-29.Wu Jianye，Zhou Haiyin.Assessment of missile fight reliability based on mixed prior distribution［J］.Journal of Spacecraft TT＆amp；C Technology，2008，27（1）：26-29.（in Chinese）

［6］ 刘强，周经纶，金光，等.基于可信度的动量轮Bayes可靠性评估［J］.宇航学报，2012，34（12）：2612-2616.Liu Qiang，Zhou Jinglun，Jin Guang，et al.Bayesian reliability estimation for momentum wheel based on credibility［J］.Joumal of Astronautics，2012，34（12）：2612-2616.（in Chinese）

［7］ 刘琦，冯静，周经纶.基于专家信息的先验分布融合方法［J］.中国空间科学技术，2004，25（3）：68-71.Liu Qi，Feng Jing，Zhou Jinglun.The fusion method for prior distribution based on expert＇s information ［J］.Chinese Space Science and Technology，2004，25（3）：68-71.（in Chinese）

［8］ 刘晗，郭波.融合多源验前信息的成败型产品可靠性Bayes评估［J］.弹箭与制导学报，2007，27（2）：338-341.Liu Han，Guo Bo.Fusion of information of multiple sources in bayesian assessment for reliability of success or failure product［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2007，27（2）：338-341.（in Chinese）

［9］ 侯敏，郭基联，李建伟.多源信息的验前分布融合方法研究［J］.火力指挥控制，2012，37（7）：57-60.Hou Min，Guo Jilian，Li Jianwei.Research on fusion method for prior distribution of multiple sources information［J］.Fire Control＆amp；Command Control，2012，37（7）：57-60.（in Chinese）

［10］张士峰，蔡洪.Bayes分析中的多源信息融合问题［J］.系统仿真学报，2000，12（1）：54-57.Zhang Shifeng，Cai Hong.Fusion of information of multiple sources in Bayesian analysis［J］.Journal of System Simulation，2000，12（1）：54-57.（in Chinese）

［11］黄寒砚，段晓君，王正明.考虑先验信息可信度的后验加权Bayes估计［J］.航空学报，2008，29（5）：1245-1251.Huang Hanya，Duan Xiaojun，Wang Zhengming.A novel posterior weighted bayesian estimation method considering the credibility of the prior information［J］.Acta Aeronautica et Astronautica Sinica，2008，29（5）：1245-1251.（in Chinese）

［12］刘琦，武小悦.Bayes方法应用中验前分布选择的一致性与可信性原则［J］.系统工程与电子技术，2010，32（11）：2356-2359.Liu Qi，Wu Xiaoyue.Principles of consistency and reliability for prior distributions selection in Bayesian method application［J］.Systems Engineering and Electronics，2010，32（11）：2356-2359.（in Chinese）

［13］邓海军，查亚兵.Bayes小子样鉴定中仿真可信度研究［J］.系统仿真学报，2005，17（7）：1566-1568.Deng Haijun，Zha Yabing.Research on applying simulation credibility into weapon system appraisal［J］.Journal of Syatem Simulation，2005，17（7）：1566-1568.（in Chinese）

TB114.3；TH707

10.16450/j.cnki.issn.1004-6801.2015.04.016

张西山，男，1987年10月生，博士研究生。主要研究方向为装备测试性分析与评估。曾发表《Hierarchical hybrid testability modeling and evaluation method based on information fusion》（《Journal of Systems Engineering and Electronics》2015，Vol.26，No.3）等论文。

E-mail：Xishan871026@sina.com

*国防十二五预先研究项目

2013-06-19；

2013-09-02