混凝土结构中PZT传感器的多功能性分析及应用*

李 旭，霍林生，李宏男，白凤龙（.大连理工大学建设工程学部 大连，603）（.大连市建筑科学研究设计院股份有限公司 大连，60）

混凝土结构中PZT传感器的多功能性分析及应用*

李 旭1，霍林生1，李宏男1，白凤龙2
（1.大连理工大学建设工程学部 大连，116023）
（2.大连市建筑科学研究设计院股份有限公司 大连，116021）

针对混凝土结构被动监测中的压电陶瓷（也称锆钛酸铅，Pb-based lead zirconium titanate，简称PZT）传感器信号的多功能特性，提出了PZT传感器不同用途信号的提取方法。根据不同功能信号的频率范围差异，通过小波Mallat分解，得到用于反映结构整体动态信息的振动信号以及局部断裂破坏引起的声发射信号，通过与加速度传感器和声发射传感器信号比较，验证了提取方法的正确性，并将该方法应用到钢筋混凝土框剪结构模型地震破坏试验的实时监测中。试验结果表明，应用该方法提取到的振动信号能准确测得结构主频率等结构的动态信息，声发射信号部分能清楚捕捉局部损伤引起的能量释放情况。应用该方法可准确提取出结构的振动信号和声发射信号，利用同一PZT传感器能够实时评估和监测结构的整体动态特性和局部损伤状况。

压电陶瓷传感器；小波分析；声发射；振动测试

引 言

压电陶瓷传感器成本低，响应快，结构简单，可靠性好，可以实现信号的收发两用，在结构损伤诊断和健康监测中应用前景广阔［1］。将压电陶瓷埋入混凝土内部或粘贴制作成的压电传感器，在混凝土结构的安全检测和损伤评估中有广泛的应用前景。赵晓燕［2］在框架剪力墙的振动台试验中，将压电传感器布置在柱脚用于被动监测，准确获取了结构的动态性能。文献［3-4］研究证明，压电传感器能获得结构的内部应力，将水泥基压电传感器应用于公路上交通流的监测，准确获得通过路面的车辆的数量和人流量。文献［5-8］开发了一种压电智能骨料，根据压电传感器收、发应力波信号的特性，用以监测混凝土内部的裂纹及损伤状况。杨永军等［9］通过压电陶瓷传感器分析了弹性波在输电塔线上的传播特性，用来识别塔线的损伤。PZT传感器的一个显著特点就是频率响应范围宽广，从零到上百兆赫兹的频率范围内，PZT传感器输出信号与表面的应力（应变）保持较稳定的线性关系［10］。因此，与其他类传感器相比，PZT传感器接收的信号是不同功能信号的重叠信号：布置在结构上的PZT传感器既可以接收到结构动态测试信号，也能采集到高频的弹性波信号。区分不同用途的PZT信号，能降低成本，增加可靠性，使PZT传感器发挥更多用途。

笔者提出了基于小波分析的PZT传感器不同功能信号的分离方法，通过小波分析的Mallat分解，得到用于振动测试的内力信号以及局部断裂引起的声发射信号，并进行了钢筋混凝土框剪结构模型的地震破坏试验。从埋置在内的PZT传感器信号分离得到不同功能的信号，说明了同一PZT传感器对结构动态特性和局部损伤监测的多功能性。

1 PZT传感器的多功能性分析

1.1 压电传感器的工作原理

压电传感器的工作原理由压电方程描述。对应力应变等力学参量，通过压电传感器以电压的形式输出。根据实际情况，对压电材料做出如下的假设：压电陶瓷视为理想的弹性材料和理想的介电材料，不存在自由移动电荷；压电陶瓷电极面为等电势面，即在压电陶瓷正负两个电极面之间形成的电场为均匀电场，且无其他方向的分量。压电方程［10］表达

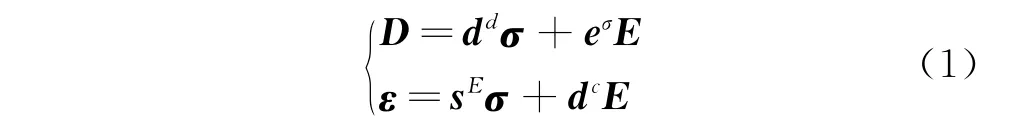
式为其中：D为电位移向量，即单位面积上的电荷；ε为应变向量；σ为应力向量；E为电场强度向量；sE为弹性柔顺常数矩阵；eσ为介电常数矩阵；上标σ和E分别表示在应力常数和应变常数条件下测量的量；dd和dc为压电常数矩阵；上标d和c用来区分正负压电效应。

实际中，dd和dc在数值上是相等的。计算方向和PZT的极化方向如图1所示。

图1 压电陶瓷的计算方向Fig.1 The positive direction of computation model

被用作传感器时，外加电场为零，极化方向为3方向的时候，电位移为其中：d31，d32，d33分别为由1，2，3方向引起的3方向的压电常数；σ1，σ2及σ3分别为1，2，3方向极化面上的应力。

以d33为主的PZT薄片结构，由于侧向面积较小，可忽略侧向内力，即σ1和σ2对输出信号的影响。输出的电压U为

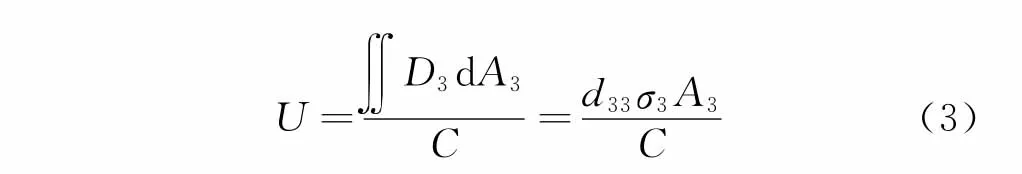
其中：A3为电极面的表面积；C为传感器电容，当与电荷放大器相连时，C表示电荷放大器电容。

埋置在结构内的PZT传感器的输出信号体现了传感器极化表面应力的变化情况。对于使用中的土木工程结构，引起埋置其内部PZT传感器极化表面内力改变的因素主要有两方面：外部激励引起的结构内力的改变；结构内部断裂释放的弹性应力波，即声发射信号。前者包含了结构的模态信息，可用获取结构的动态特性，频率集中在零到上百赫兹的低频范围，声发射的信号频率为1 000 Hz～10 MHz的高频成分。PZT传感器的频率响应范围广，若数据采集设备的采样频率足够高，PZT的输出信号将会覆盖用于振动测试的内力信号以及内部断裂引起的声发射信号。两者在频率范围内并不冲突。通过数字信号处理技术将不同功能特性的信号分离，实现PZT传感器的多功能特性。

1.2 基于小波分析的PZT传感器不同功能的信号

提取

小波分析［11-13］是20世纪80年代末发展期起来的数学分支。小波分析的Mallat算法是一种塔式多分辨率分析与重构的快速算法，是一种实现不同功能PZT传感器信号的方便工具。Vj为尺度函数φ（t）经过伸缩和平移之后得到函数族｛φj，n（t）｝n∈Z构成的正交规范基。信号f（t）的近似信号fAj（t）为信号f（t）在Vj上的正交投影，其展开式的系数aj（n）为近似部分的小波系数。类似的，Wj为小波函数ψ（t）经过二进伸缩和平移之后得到函数族｛ψj，n（t）｝n∈Z构成小波空间的正交基。细节信号fDj（t）为f（t）在Wj上的正交投影，其展开式系数dj（n）为细节部分的小波系数。在Mallat算法中，将用数字滤波器h（n）和g（n）代替尺度函数和小波函数，g（n）和h（n）分别为

Mallat分解算法表达式为k

Mallat分解算法的过程如图2所示。其中：j+ 1层近似部分的小波系数aj+1为通过aj与分解滤波器h卷积并隔点采样得到；j+1层细节部分的小波系数dj+1为通过aj与分解滤波器g卷积并隔点采样得到。

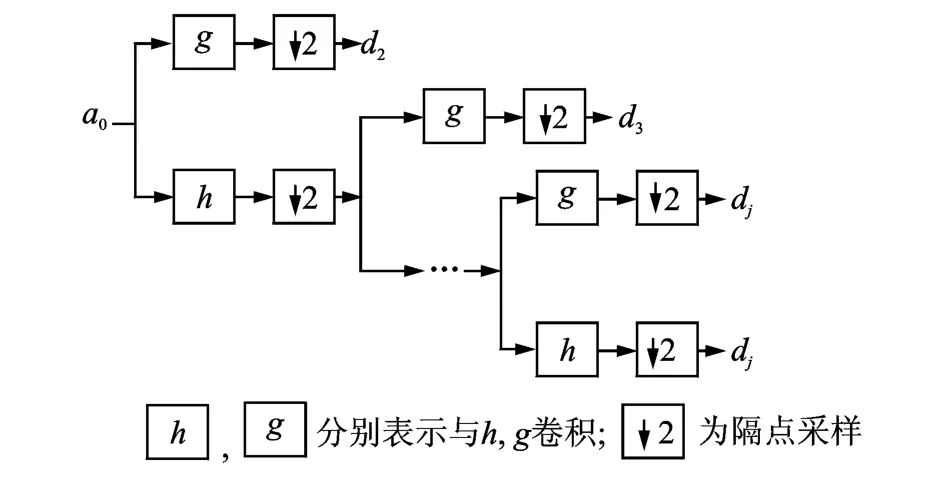
图2 Mallat分解算法Fig.2 The Mallat algorithm

将PZT信号fpzt（t）进行j级Mallat分解，fAj（t）为第j级分解后逼近系数aj的重构信号，fDj（t）为j级分解后细节系数dj的重构信号。结构振动信号成分SV取PZT信号小波分解后近似部分

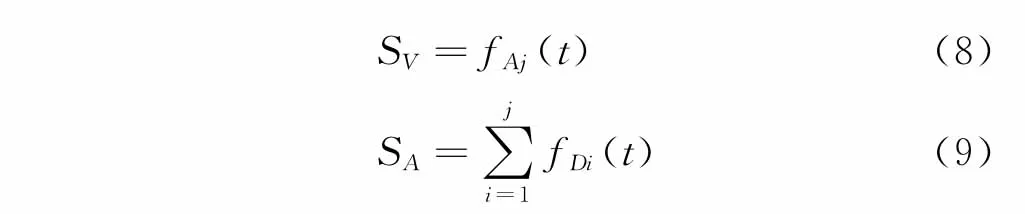
若采样频率为fc，根据采样定理，信号f（t）的频率范围为0～fc/2，则SV的频率范围为0～fc/2j+1，SA的频率范围为fc/2j+1～fc/2。二者的频率界限为fc/2j+1，选择合理的j才能准确提取PZT传感器不同功能的信号。因此，j的选择既要满足fc/2j+1大于测试所需结构的各阶模态频率，又要使fc/2j+1小于声发射信号频率的下限。在土木工程结构的模态测试中，通常采样频率为1 k Hz就可以满足测得各阶模态主频率的需要。为了准确提取PZT传感器不同功能的信号，分解层次j的选取应尽可能接近log2（fc/1 000）。

小波基的选择会影响PZT传感器不同功能信号的提取效果。不同的小波基具有不同的时频特性，同一信号由不同小波基分解的信号也存在差异。根据PZT传感器信号的特点，为了准确分离不同功能的PZT传感器信号，避免频率混叠，所选的小波基应该在时域内具有紧支撑性，在频域具有快速衰减性，为具有一定消失矩的正交或双正交小波基。因此，Daubechies小波、Symlets小波和Coitlets小波都是适用于PZT传感器信号提取的小波基。

图3 SV与加速度的时频域信号Fig.3 The time and frequency domain of accelerative signal and SV

图3为框架剪力墙模型地震模拟试验中，同一位置处加速度传感器与由PZT传感器信号得到的的小波系数重构信号，声发射信号成分SA用PZT传感器信号的细节信号累加来表示SV比较。可以看出，PZT信号的振动信号成分与加速度信号的波形相近，SV的前3阶频率为4.27，17.7，31.13 Hz，加速度信号的前3阶频率为4.25，17.75，30.77 Hz，最大相对误差不超过0.5％，SV较准确地反映了结构的模态频率。此外，在钢筋混凝土柱中相同位置处布置的声发射传感器和PZT传感器。图4为由PZT传感器信号得到的SA与声发射传感器测得的声发射信号的对比，声发射测得信号的主频率和SA的主频率分别为125 k Hz和124.7k Hz，相对误差为0.24％。声发射测试中的一些特性参数都是由时域波形得到的，故进一步分析二者时域波形的相似程度。互相关函数描述了两个信号间的相关程度，图5为SA和声发射传感器信号的互相关函数。可以看出，在零相位时刻，互相关函数为0.978 2，接近1，两传感器的时域波形具有非常好的相似性。不管从信号的时域特性还是频域特性分析，SV和SA分别与振动信号和声发射信号有良好的相似性。通过式（8），（9），可以将PZT信号中的振动信号和声发射信号分离出来，实现PZT传感器的多功能性。

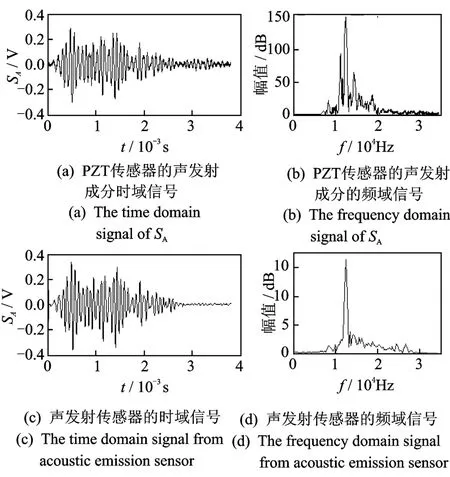
图4 SA与声发射的时频域信号Fig.4 The time and frequency domain of acoustic emission signal and SA

图5 声发射传感器信号与SA的互相关函数Fig.5 The cross-correlation function between acoustic emission signal and SA

2 多功能性PZT传感器在框架剪力墙模型地震破坏试验中的应用

进行了钢筋混凝土框架剪力墙结构的振动台破坏的PZT传感器实时监测试验，根据PZT传感器的多功能性来分析整体和局部破坏情况。模型为1/5尺寸的双向双跨三层钢筋混凝土偏心框架-剪力墙结构，采用埋入式PZT传感器，编号为E-1到E-7，传感器布置如图6所示。模型中的受力纵筋采用3 mm的镀锌铁丝，0.9 mm的镀锌铁丝作为箍筋，剪力墙和板中的配筋直径为2 mm、间距为20 mm的双层镀锌铁丝网，结构采用微粒混凝土进行浇筑。基础底座采用C30混凝土饶筑。柱子的截面尺寸为80 mm×80 mm，梁截面为50 mm× 100 mm，板厚为30 mm。图7为试验的模型图。试验是在大连理工大学海岸与近海工程国家重点实验室的地震模拟振动台上进行的，在水平方向（y方向）和竖直方向（z方向）同时进行激振。采用1940 年El-Centro波南北分量和竖向分量作为本次试验的地震动输入，如图8所示。输入的地震波工况如表1所示，共分13组工况输入，每种工况下地震波具有不同的幅值。用dSPACE系统采集PZT信号，采样频率为10 k Hz，并同步测量了每层的加速度。

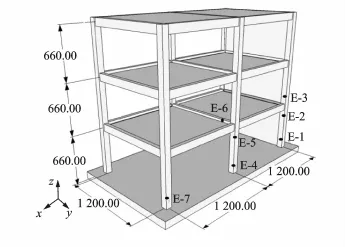
图6 模型的尺寸及传感器布置（单位：mm）Fig.6 The dimensions of model and the distribution of PZT sensors（unit：mm）

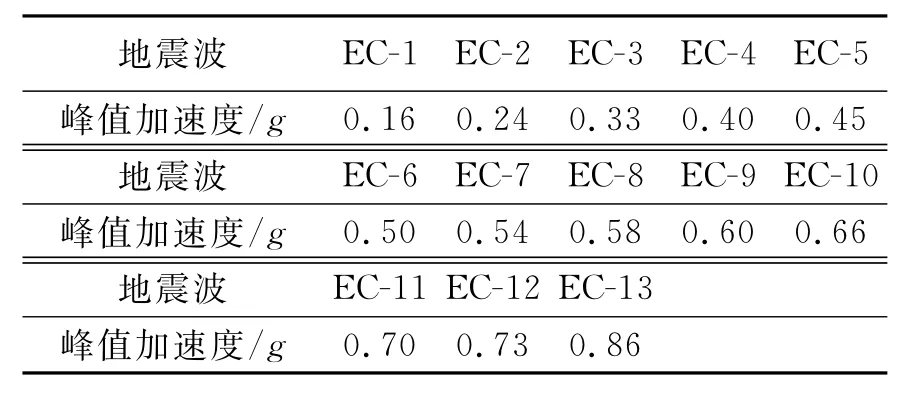
表1 所输入的地震波Tab.1 The earthquake wave list

图7 试验照片Fig.7 The experimental photo

同步采集了PZT及速度传感器的数据，选择Daubechies25小波基进行4级小波分解，根据式（8），（9）获得结构振动测试的信号和声发射信号。图9为EC-13加载得到的E-1的PZT传感器的信号以及分解得到的SV和SA。

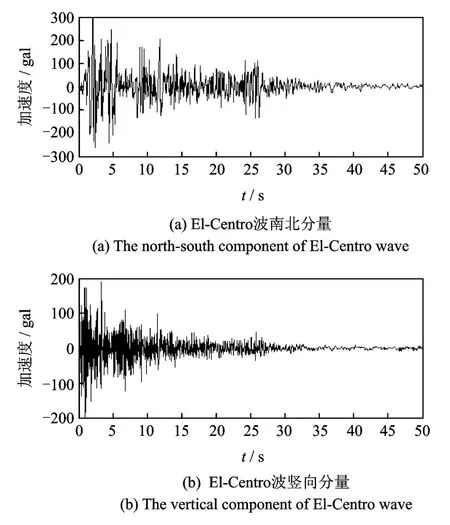
图8 El-Centro波Fig.8 The El-Centro wave

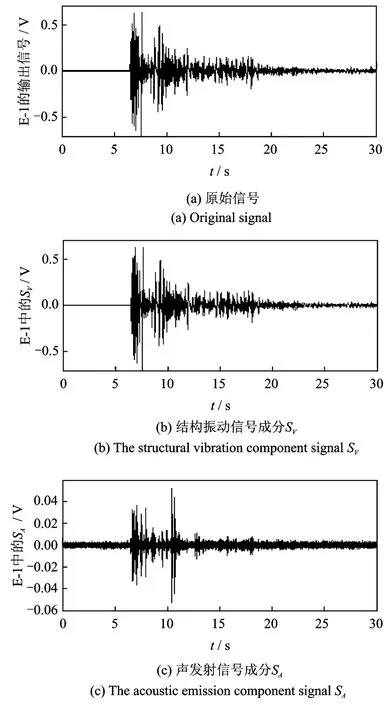
图9 EC-13加载得到的E-1的PZT传感器的信号以及分解得到的SV和SAFig.9 The signal of E-1 and the SVand SAduring EC-13 loading process

图10为各级加载中，2层加速度传感器和E-2得到的前三阶频率随加速度峰值变化的曲线。可以看出，E-2得到的前三阶主频率与加速度传感器的测量结果相似，随着峰值加速度的增加，结构破坏不断加剧，频率逐渐降低。

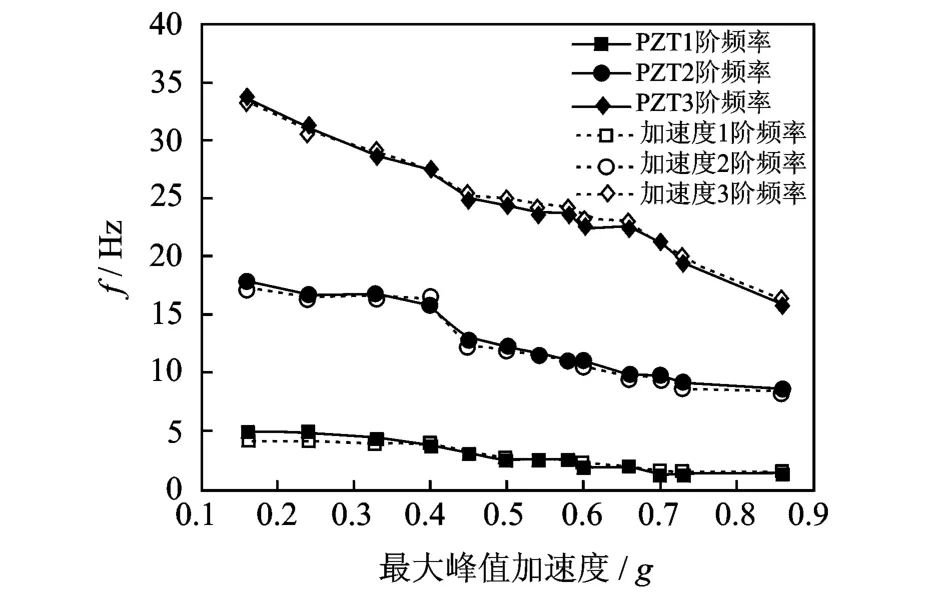
图10 前三阶频率曲线Fig.10 The curve of first three frequencies

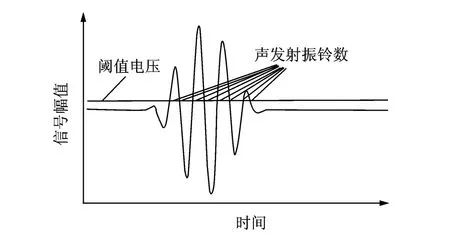
图11 声发射振铃数的示意图Fig.11 The schematic diagram of acoustic emission counts

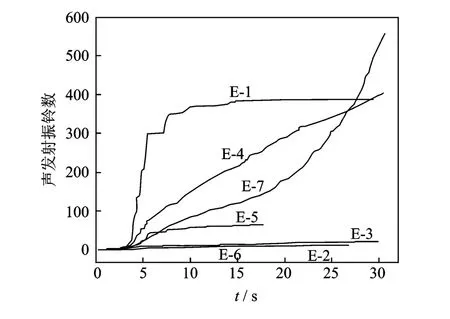
图12 EC-13加载过程中E-1～E-7声发射振铃数Fig.12 The acoustic emission count of E-1to E-7 during EC-13 loading

声发射的振铃数N为声发射信号中通过某一阈值的次数，如图11所示。声发射的振铃数体现了声发射信号能量的大小［14］，N越大，声发射信号释放的能量越大，损伤越严重。图12记录了EC-13加载过程中E-1到E-7声发射振铃数的变化，其中阈值为0.005 V。可以看出，加载的地震波为EC-13时，整个加载过程中E-2，E-3，E-6的振铃数分别为12，22和11，说明E-2，E-3，E-6附近在EC-13的加载历程仅发生了微小的破坏。E-1，E-4，E-7发生较严重的破坏，15 s后，地震加速度的峰值已经过去，E-1的振铃数已经不再增加，而E-4和E-7的振铃数持续增加，说明E-4和E-7附近的破坏已经相当严重，即使很小的外部荷载也会使裂纹继续拓展。图13为所有地震波加载完成后，E-1～E-7总的声发射振铃数。比较结构底端的传感器信号，E-7的累计振铃数最多，E-4次之，E-1振铃数相对较少，说明边柱的底部破坏较严重，中柱次之，而与剪力墙相连的柱底破坏较轻。这是结构因为沿着x方向的刚度不均匀，剪力墙一侧刚度较大而边柱一侧的刚度较小，结构发生扭转，导致边柱的变形要大于剪力墙部分的变形，因此沿着x方向破坏变的越来越严重。通过PZT传感器得到的声发射信号能监测传感器附近的构件的破坏状况，判断结构的局部损伤。

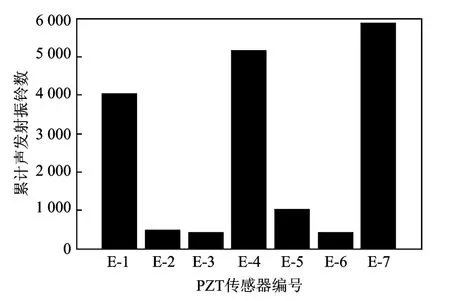
图13 E-1～E-7总的声发射振铃数Fig.13 The total acoustic emission count of E-1 to E-7

3 结 论

1）在小波分析的基础上，将不同用途的PZT信号加以分离，结合加速度信号和声发射信号，可得到结构的振动信号用于测试结构的动态参数以及局部断裂引起的声发射信号，实现了PZT传感器用途的多功能性。

2）从PZT信号中分离出来的用于结构动态测试的信号分量，准确监测了钢筋混凝土框架剪力墙模型随着地震荷载峰值加速度增加导致的前三阶频率的变化，可用于评估结构的整体损伤。从PZT信号中分离出来的用于捕捉断裂信息的声发射信号，能够评估结构的局部损伤。该方法可使同一种传感器实现不同用途，降低成本，减少维护，可同时用于评估结构的整体及局部损伤状况。

［1］ 王秋婧.压电陶瓷驱动器力学模型理论与试验研究［D］.沈阳：沈阳建筑大学，2011.

［2］ 赵晓燕.基于压电陶瓷的结构健康监测与损伤诊断［D］.大连：大连理工大学，2008.

［3］ 杨晓明.土木工程结构的性能监测系统与损伤识别方法研究［D］.天津：天津大学，2006.

［4］ Li Zhongxian，Yang Xiaoming.Application of cementbased piezoelectric sensors for monitoring traffic flows ［J］.Journal of Transportation Eengineering，ASCE，2006，132（7）：1-9.

［5］ Song Gangbing，Olmi C，Gu Haichang.An overheight vehicle-bridge collision monitoring system using piezoelectric transducers［J］.Smart Materials and Structures，2007，16（2）：462-468.

［6］ Song Gangbing，Gu Haichang，Mo Yilung.Smart aggregates：multi-functional sensors or concrete structures-a tutorial and a review［J］.Smart Materials and Structures，2008，17（3）：1-17.

［7］ Gu Haichang，Song Gangbing，Dhonde H.Concrete early-age strength monitoring using embedded piezoelectric transducers［J］.Smart Materials and Structures，2006，15（6）：1837-1845.

［8］ Song Gangbing，Gu Haichang，Mo Yilung，et al.Concrete structural health monitoring using embedded piezoceramic transducers［J］.Smart Materials and Structures，2007，16（4）：959-968.

［9］ 杨永军，李华东，裘进浩.弹性波在高压输电线中的传播特性［J］.振动、测试与诊断，2012，32（2）：214-217.Yang Yongjun，Li Huadong，Qiu Jinhao.Propagation characteristics of elastic wave in the overhead transmission cable［J］.Journal of Vibration，Measurement ＆amp；Diagnosis，2012，32（2）：214-217.（in Chinese）

［10］Sirohi J，Chopra I.Fundamental understanding of piezoelectric strain sensors［J］.Journal of Intelligent Material Systems and Structures，2000，11（4）：246-257.

［11］Yi Tinghua，Li Hongnan，Sun Hongmin.Multi-stage structural damage diagnosis method based on“energydamage”theory［J］.Smart Structures and Systems，2013，12（3-4）：345-361.

［12］沈松，应怀樵，刘进明.小波变换在振动信号分析中的工程解释与应用［J］.振动、测试与诊断，2000，20（4）：259-263.Shen Song，Ying Huaiqiao，Liu Jinming.An engineering interpretation to wavelet transform and its applications to the analysis of vibration signals［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2000，20（4）：259-263.（in Chinese）

［13］唐晓初.小波分析及其应用［M］.重庆：重庆大学出版社，2006：32-54.

［14］Carpinteri A，Lacidogna G，Niccolini G，et al.Critical defect size distributions in concrete structures detected by the acoustic emission technique［J］.Meccanica，2008，43：349-363.

TU375；TP212.9；TH165+.3

10.16450/j.cnki.issn.1004-6801.2015.04.018

李旭，男，1985年12月生，博士研究生。主要研究方向为结构健康监测与智能材料。曾发表《钢筋混凝土柱加载试验的AE监测研究》（《振动与冲击》2014年第33卷第20期）等论文。

E-mail：lx3818262@163.com

*国家重大基础研究发展计划（“九七三”计划）资助项目（2015CB057704）；国家自然科学基金创新群体资助项目（51121005，51421064）；大连市建设科技计划资助项目

2013-07-17；

2013-10-08