高填方涵洞顶部土体的成拱效应及计算分析
马 莉
(山西省交通规划勘察设计院,山西 太原 030012)
0 引言
由于山西地处黄土高原,沟壑纵横,地形复杂,随着高速公路规划网的不断细化,很多条高速公路都修建于山岭重丘区。由于高等级公路线性标准的要求和地形的限制,使得山区高速公路的填土高度普遍较大,高填方涵洞也随之增多。与低填方涵洞相比,高填方涵洞具有填土荷载大的特点,再加上山区特殊地质条件的影响,涵洞的受力及变形特性极为复杂,很多涵洞都出现了开裂,甚至垮塌,严重影响公路的正常运营,给人民的生命财产安全造成极大威胁。而涵洞顶部土压力的精确计算是涵洞结构设计中的重中之重,但是相关研究表明目前的土压力计算理论均不能够准确估计高填方涵洞顶部土压力分布状态。本文基于试验数据,合理考虑“拱效应”原理,分析了高填土条件下的涵洞顶部土体的土压力变化特点,为涵洞的结构设计提供参考。
1 涵洞顶部土体的成拱效应
“拱效应”是土木工程中一个普遍存在的现象[1-2],由于存在“拱效应”,高填方涵洞顶部土压力的计算并不能简单地仅仅归结于土的重力计算问题。合理考虑“拱效应”对涵顶土压力的影响程度是精确计算高填方涵洞顶部土压力的首要问题。
本文选取山西某山区高速公路圆管涵为研究对象,结果表明:高填方涵洞顶部存在明显的“拱效应”。涵顶土压力随着填土高度的不断增大以非线性规律逐渐增大。因此研究一种合理考虑“拱效应”的土压力计算方法,才能使高填方涵洞的结构设计更为经济合理。
2 高填方涵洞顶部竖向土压力研究
本文以试验数据为依据,运用回归分析法对涵顶土压力随填土高度增大的变化规律进行研究。
2.1 试验方法设计和分析
选取山西某山区高速公路典型圆管涵涵洞断面为试验对象,沿涵顶轴线位置埋设5个土压力盒以测试涵顶竖向土压力。测试结果表明,涵顶竖向土压力随填土高度的增大表现出显著的非线性增大规律。
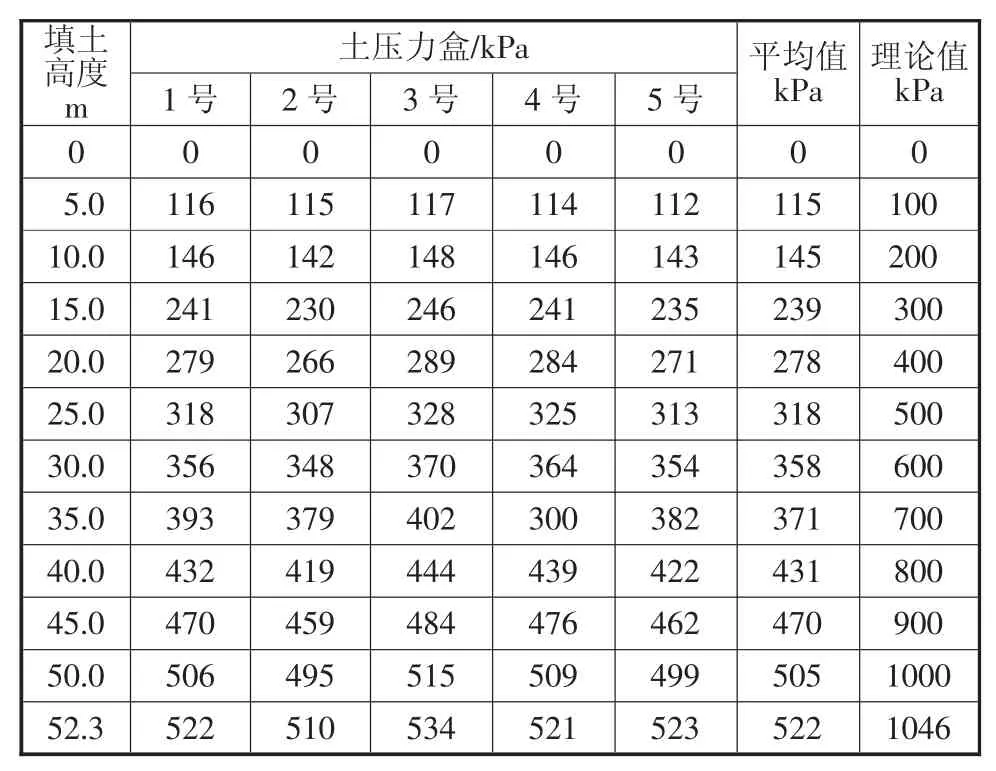
表1 不同填土高度下的涵顶竖向土压力测试结果
2.2 涵顶土压力计算公式非线性回归分析
试验数据表明,高填方涵洞顶部的土压力随填土高度增大呈显著的非线性增大规律。本文运用以下简单实用的模型作为高填方涵洞顶部土体的土压力计算公式,结合试验数据计算出回归系数,给出涵顶土压力计算公式。
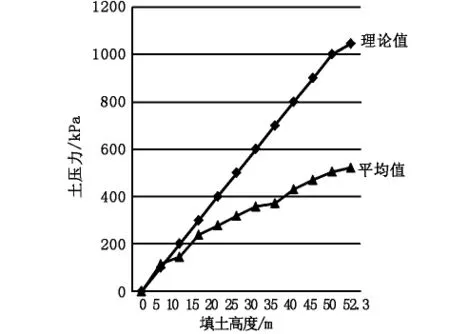
图1 涵顶土压力理论计算值和测试值对比图

式中:a、b为回归系数;γ为填土容重,kN/m3;H 为填土高度,m。
对式(2)回归计算得:a=1.198,b=0.783.
3 实例分析
运用马斯顿法[3-4]、土柱法[5]、普氏理论、太沙基理论以及本文的土压力计算公式,分别计算不同填土高度下涵洞顶部的土压力,以便于对各种理论公式的适用性进行分析研究。
计算参数如下:内摩阻角φ=30°,内聚力c=20 kPa,填土容重 γ=20 kN/m3,涵洞半径a=2.7 m。
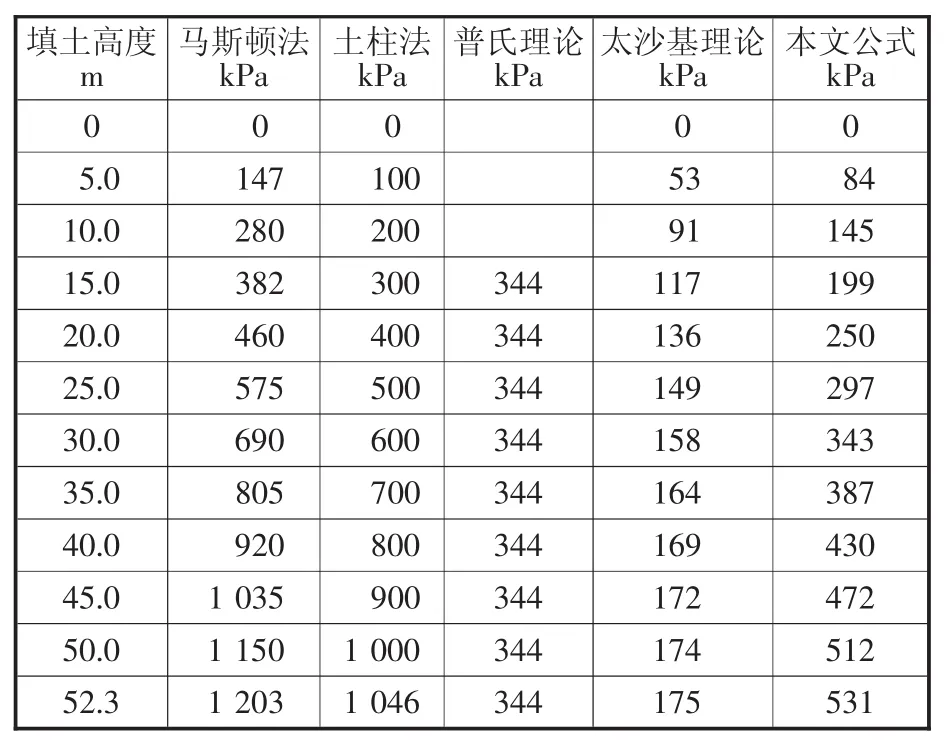
表2 不同理论公式下涵顶竖向土压力的计算结果
由表2可见,马斯顿法或土柱法由于未考虑拱效应,计算出的土压力过大,以此为依据进行涵洞结构设计将会造成安全系数过大,过分保守而不经济;太沙基理论以岩体传力为计算基础,填土达到一定高度时,压力将不再往下传递,计算出的土压力最小,如以此理论计算的土压力为依据进行设计,将会导致结构不安全;普氏理论假设涵洞上方有一个稳定的土拱,考虑了拱效应,结构承担的荷载为土拱下不稳定的土体重量,计算的土压力不随填土高度变化而改变,且未考虑在填土增加过程中仍有部分土压力传递到涵顶的情况。而本文推导出的非线性计算公式,合理考虑了“拱效应”,即充分考虑高填方涵洞上方存在拱效应以及此土拱效应不稳定的特点,在填土增加过程中仍有部分土压力传递到涵顶,其计算的土压力高于太沙基理论,但又显著低于不考虑土拱效应的土柱法和马斯顿法,使计算结果和实际情况较为接近,设计的涵洞结构既经济又安全。
4 结论
a)本文回归分析的涵顶土压力计算公式合理考虑了“土拱效应”对土压力的影响,使计算公式计算出的涵顶土压力结果接近实际情况,计算结果较为合理。
b)本文的土压力计算公式简单实用,只需确定填土高度和填土容重两个计算参数即可,便于广泛应用。
c)本文的土压力计算公式是基于现场实验反推出来的半经验公式,使用具有一定局限性,更广泛使用的“通用公式”,需要更多的试验数据支持。
——结构相互作用的影响分析

