非线性互补问题光滑化拟牛顿算法的超线性收敛性

牛潇萌

（赤峰学院 数学与统计学院，内蒙古 赤峰 024000）

1 算法

考虑P0函数非线性互补问题：求x∈R"，使得

其中F是连续可微的P0函数.

使用如下光滑函数[1]：

设 z=(μ,x)∈Rn+1,

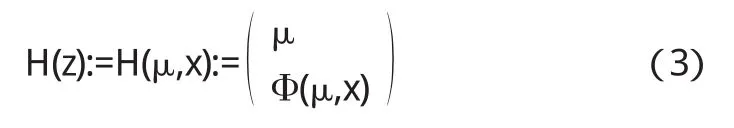
其中

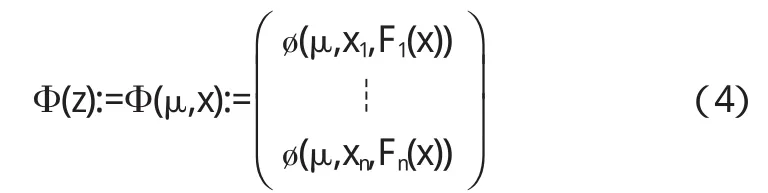
经简单计算易知H(z)的Jacobian矩阵为

其中塄xΦ(z)T:=[μD1(z)+D2(z)]+[D1(z)+μD2(z)]F'(x),

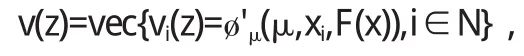
且 D1(z):=diag{a1(z),…,an(z)}，

设 γ∈(0,1).定义函数 ρ:Rn+1→R+为ρ(z)=γmin{1,||H(z)||2}.

算法1[2]（光滑化拟牛顿算法）

步1 若 ||H(zk)||=0，停.否则，设 ρk:=ρ(zk).若 μk>ρkμ0，解方程 H(zk)+Gk△zk=ρk赞得 △zk=(△μk，△xk)，否则，令 △zk=(△μk，△xk):=（0，△xk），并解方程组 Φ(zk)+Bk△xk=0得 △xk，其中 Gk∈R(n+1)×(n+1)定义为塄且 Bk是塄xΦ(zk)T的一个近似.

步2 若 ||H(zk+△zk)||≤α||H(zk)||-σ1||△zk||2，则设 λk:=1，转步4.

步3 设 λk是取自集合{1,δ,δ2,…}使得 λ=δi满足如下线搜索的最大数

步4 zk+1=(μk+1,xk+1)=zk+λk△zk

步5 用如下Broyden-like校正公式修正Bk得Bk+1：

其中 sk=λk△xk=xk+1-xk，yk=Φ(μk,xk+1)-Φ(μk,xk)，参数 θk满足 |θk-1|≤且 Bk+1非奇异.

步6 令k=k+1，转步1.

2 超线性收敛性分析

引理 1[3]设 H:R++×Rn→Rn+1，Φ：R++×Rn→Rn+1和 v:R++×Rn→Rn+1分别由（3），（4）和（6）定义，则

（i）Φ 在 R++×Rn是半光滑的；

（ii）H是局部Lipschitz连续的且在R++×Rn是半光滑的.进一步，F'(x)在Rn上是Lipschitz连续的，则H在R++×Rn是强半光滑的.

为证明超线性收敛性需要如下假设条件：

假设条件B

（i）由算法1产生的序列{zk}收敛到H(z)=0的解z*=(μ*,x*)=(0,x*)，其中 H(z)由（3）定义，且 x*是非线性互补问题（1）的严格互补解；

(ii)塄xΦ(z*)非奇异.

引理 2[3]假设 H:Rn+1→Rn+1和 Φ:Rn+1→Rn分别由（3）和（4）定义.则

（ⅰ）Φ 在任一点 z=(μ,x)∈Rn+1，μ≠0是连续可微的.

（ⅱ）H在任一点 z=(μ,x)∈R++×Rn是连续可微的，其Jacobian矩阵由（5）定义.如果 F是一 P0函数，则塄xΦ(z)在R++×Rn是非奇异的，从而H'(z)在R++×Rn是非奇异的.

定理1 假设条件A，B成立，{zk=(μk,xk)}由算法1产生.则存在一常数 ζ>0和一指标k軈，使得当 ζk≤ζ且 k≥时，有λk=1，其中.此外，对于满足 ζk≤ζ的 k≥，不等式成立.

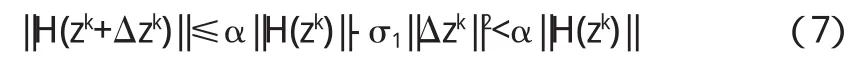
证明由算法1的步2可知，仅需证明存在一正常数ζ，使得ζk≤ζ且k充分大时式（7）成立.设xk+tsk)Tdt.因为μk>0，所以由引理 2（ii）可知 Ak+1非奇异.由假设条件 B（i）可知 Ak+1趋于塄xΦ(z*)，因为塄xΦ(z*)和 Ak+1非奇异，所以存在一常数M2>0，使得对充分大的kM2，其余的证明由[4]引理4.4类似可证.

定理2 设假设条件A，B成立，{zk}由算法1产生，{zk}是超线性收敛的.

证明由[4]定理4.1类似可证.

3 数值实验结果

本节提供数值实验结果.结束准则为

||H(zk)||≤ε=10-6

相关参数取 ε=10-6，α=0.9，δ=0.9，σ1=0.8，μ0=10-3，γ=0.2，η=0.5.

算例 1[5]（HS35）这是Hock-Schittkowski收集的第35个问题.这个问题定义为

minf(x)=2x12+2x22+x32+2x1x2+2x1x3-8x1-6x2-4x3+9

s.t.3-x1-x2-x3≥0

xi≥0，i=1，2，3.

这是一个凸规划问题，它的Karush-Kuhn-Tucker最优性条件导出一个4维单调互补问题CP（F），其中F(x)定义如下：

表1 算例1的计算结果

算例2[6]考虑如下4维非线性互补问题NCP（F），其中F(x)定义如下：

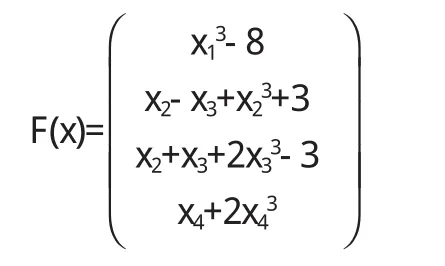
此问题有唯一退化解x*=(2,0,1,0)，计算结果见表2.

表2 算例2的计算结果

算例3[7]这是一组n维线性互补问题，设F(x)=Mx+q，n阶方阵M和n维向量q定义如下:

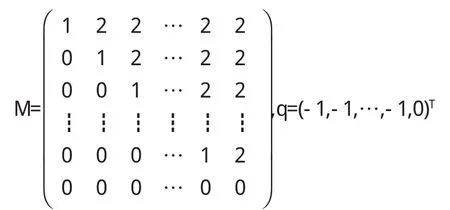
M是P0矩阵，取初始点x0=(0,…,0)T，计算结果见表3.

表3 算例3的计算结果

〔1〕Huang Z,Han J,Xu D,Zhang L.The non-interior continuation methods for solving the -functin nonlinear complementarity problem[J].Science in China,2011,44:1107-1114.

〔2〕牛潇萌.非线性互补问题的光滑化拟牛顿算法[J].计算机工程与应用,2013(18):33-35.

〔3〕Zhang L P,Han J Y,Huang Z H,Superlinear/Quadratic one-step smoothing New ton method for -NCP[J].Acta Mathematica Sinica,2005(21):117-128.

〔4〕Ma C F,Chen L J,Wang D S.A globally and superlinearly convergent smoothing Broyden-like method for solving nonlinear complementarity problem[J].Applied Mathematics and computation.2008(198):592-604.

〔5〕Hock W,Schittkowski K,Test examples for nonlinear complementariy problems [J].Computati-onal Optim izationand Applications,1996(5):155-173.

〔6〕Yamashita N,Fukushima M,Modified New ton methods for solving a semismooth reformulati-on of monotone complementarity problems[J].Mathematical Programm ing,1997(76):469-491.

〔7〕Chen X J,Ye Y Y,On smoothing methods for the P0-matrix linear complementarity problem[J],SIAM J.Optim.,1997(7):403-420.