基于振动特性的含冲击损伤复合材料检测的有限元模拟
杨鹏飞,宁 宁,詹绍正,何 潇
(中国飞机强度研究所,西安 710065)
当前,飞机复合材料结构损伤容限的设计准则是基于损伤无扩展概念来进行的,而试验结果表明,复合材料对外来冲击和意外损伤较敏感。为确保结构安全,必须运用严格的检查手段来检测可能出现的冲击损伤。然而,现有的技术手段需要逐点扫查,检测效率低,故需要建立一种快速、简洁、实用的无损检测方法,以便能够及时地获取材料或结构中损伤位置、损伤程度等信息,并能对结构的剩余强度做出评估。
近年来,出现了比较多的基于振动特性的材料和结构损伤的研究,DOEBLING[1],CARDEN[2]等考虑了结构的质量、阻尼和刚度等参数对结构振动响应的影响。ZOU 等[3],DELLA 和SHU[4]等研究了复合材料分层的出现对结构强度改变和振动响应的影响。对于复合材料的振动分析,主要通过频响函数,振动频率,模态曲率,应变能等损伤指标对其进行分析。各种损伤指标分析时都有自己的优势和不足,需要进一步对其完善。笔者主要通过以模态固有频率和改进的模态曲率损伤因子作为损伤指标对含冲击分层损伤的复合材料层压板进行分析。
1 损伤识别原理
1.1 模态固有频率
对于含损伤的结构,笔者主要考虑以固有频率和改进的模态曲率作为损伤识别指标。
由于材料或结构刚度发生变化,其固有频率也发生相应的变化。所以,模态固有频率变化率可作为其损伤检测的一个指标。

式中:fifdi分别表示没有损伤和含损伤复合材料板的固有频率。
模态固有频率作为损伤指标对于结构的损伤有一定的感知能力,但对于结构损伤的具体定位并不十分明晰,不同部位的损伤可能具有相同的模态固有频率。
1.2 模态曲率损伤因子
模态曲率作为一个重要参数对损伤识别也具有重要的意义。在位移模态振型的基础上,依据中心差分法可以近似计算出模态曲率振型[7]:

式中:kqi(φi)为局部模态曲率;φqi为测点的模态振型;φ(q+1)i和φ(q-1)i分别为测点前一相邻位置和后一相邻位置的模态振型;l为测点到相邻两侧点之间的距离的平均值。
通常取模态曲率的差值(MCD)来进行损伤识别
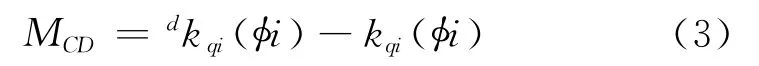
式中:kqi(φi)和dkqi(φi)分别为结构未损伤和损伤情况下的局部模态曲率。
在此基础上,笔者考虑了局部曲率变化在整体结构中的影响,给出了以下方程:

式中:m为模态阶数,MCDF为在某一阶情况下结构损伤的局部模态曲率损伤因子,′MCDF为总体阶数下的模态曲率损伤因子。
2 有限元模型的建立
所采用的复合材料为T300/QY9811,材料几何尺寸为150mm×100mm×0.5mm,三边自由,一边固支。粘结单元采用COH3D8单元,单层纤维板采用3D 应力单元,单元尺寸约为2.25 mm2,可以满足对单元精度的要求。
对于冲击损伤的引入,笔者主要考虑分层对模态的影响,通过引入粘结单元的办法引入冲击损伤。粘结单元的损伤模式中,近似认为材料两个方向的断裂能相等。通过超声C扫描和B扫描,确定损伤位置和尺寸,C扫描的揭层显示可以描述分层的形状,B扫描可以给出损伤在厚度方向的轮廓,依次得到损伤的尺寸[5],将其简化处理记录典型损伤形式并引入有限元模型当中,笔者所引入的损伤轮廓及简化方式如图1所示。

图1 冲击损伤C扫描及简化模型图
经冲击损伤数据的分析和阶层显示可以了解到:分层损伤主要成花生壳形状的分布形式[6];能量较小时,花生壳形状表现不明显;随着冲击能量的增大,花生壳形状表现越来越明显,并沿着纤维方向分布。不同层的损伤主要考虑分层损伤,通过将损伤区域的粘结单元删除,上下层板之间没有连接,以此来模拟分层损伤。各层的损伤形式为花生壳形状,从上到下的轮廓模式近似按照B扫描的形式给出,从上到下损伤面积逐渐扩大,但底部损伤面积又稍微减小一些。
对于模态求解采用Lanczos法,提取15阶模态参数;之后,分别提取复合材料层压板整体的模态频率和模态振型,同时在复合材料层压板表面设置15个测点,提取其在X,Y,Z3个方向的模态振型;进而计算模态固有频率变化率和模态曲率损伤因子。测点位置如图2所示。

图2 测点分布图
3 结果分析和讨论
3.1 不同损伤程度的复合材料损伤指标的变化
3.1.1 模态固有频率的变化
针对4 种不同损伤程度的复合材料层压板进行模态分析。损伤程度分别为1 8mm×2 0mm,39mm×41mm,58mm×60mm,80mm×79mm。比较4种损伤情况下,模态固有频率差值和模态曲率损伤因子的变化。
从图3可看出,随着损伤程度的增加,由于材料强度的减小,模态频率即材料的固有频率变化率逐渐增大。同时还可看出,对于铺层情况相同损伤程度不同的复合材料,随着损伤程度的增加,6、8阶的固有频率变化率也随之增大。这主要是因为增大的损伤导致了材料在新的部位出现损伤,新的地方出现强度减弱的趋势。同时各种损伤程度下固有频率变化率都在4、10、12、14阶情况下变化较大,具有一致性。

图3 不同损伤程度下的模态固有频率变化率
图4列出了没有损伤和第4 种损伤程度的4、8、12、14、15阶模态图,从图中可以看出其模态的差异性。在这对于试验测定频率变化所选取的模态阶数有一定的指导意义。
3.1.2 模态曲率损伤因子的变化

图4 无损伤和第4种损伤情况的模态位移振型
提取15阶z方向模态位移振型数据进行分析。这里取测点12处测点的实际位置,分别计算其模态曲率损伤因子。
由图5可见,随着损伤程度的增加,模态曲率损伤因子也随之增大;同时,通过模态曲率可看出振型变化的位置,进而可确定损伤的位置。由于冲击损伤主要集中在中间测点处,四种情况下,最大的模态曲率损伤因子位于8测点,所以模态损伤因子作为损伤指标能比较准确地给出损伤位置。还可看出,当损伤较小时,中间测点旁边的测点也较大,损伤识别不是很明显,这主要是因为损伤较小时,模态曲率变化不大,周围测点的数据会对损伤的判别有一定的干扰。随着损伤程度的增加,中间测点和周边测点的模态曲率的差异性变大,对损伤位置识别的灵敏度增强。
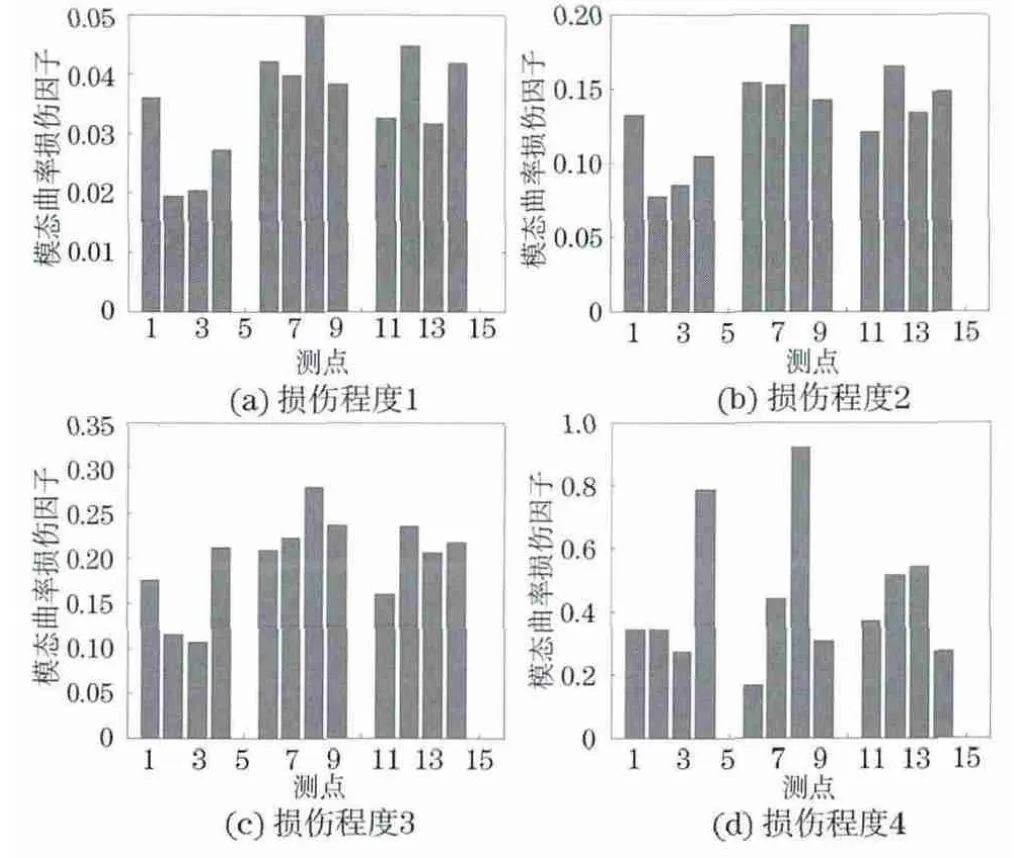
图5 不同损伤程度的模态曲率损伤因子
3.2 不同铺层复合材料损伤指标的变化
3.2.1 模态固有频率的变化
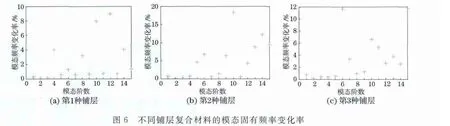
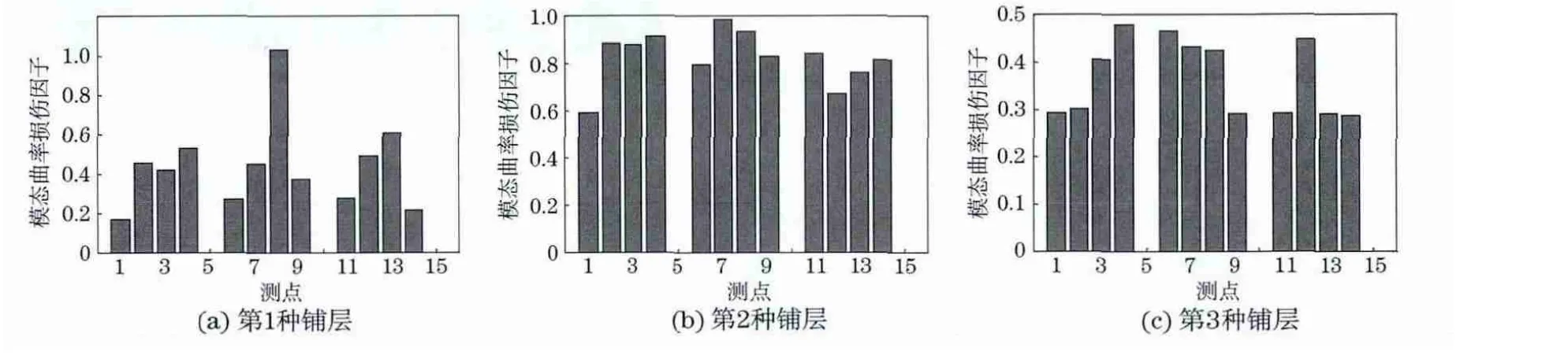
图7 不同铺层复合材料的模态曲率损伤因子
针对不同铺层的情况,选取各层相同的40mm×40 mm 的损伤面 积,分别选取[0/45/-45/90],[0/90/0/90],[45/0/-45/0]三种情况的铺层(数字表示层压板单层的铺设角度),分别考虑其对应的模态固有频率变化率和模态曲率变化损伤因子,其结果如图6,7所示。
从图6可看出,随着铺层情况的变化,模态频率即材料的固有频率变化率也发生了变化。同时还可看出,对于损伤情况相同铺层不同的复合材料,第一种铺层的固有频率变化率最小,第二种铺层的固有频率变化率最大;这主要是因为铺层不同的复合材料层压板对于相同损伤拥有不同的强度变化。模态曲率变化率的规律性并不明显,但固有频率变化率都在10阶处具有较大的变化率,具有一致性。这对于损伤的发现和检测具有指导意义。
3.2.2 模态曲率损伤因子的变化
从图7可看出,第一、二、三种模态的曲率损伤因子最大处分别位于8,7,4测点处,基本都位于冲击损伤处,位置基本正确;但第一种容易识别,第二种和第三种的识别相对较难一些,这主要是因为损伤面积较小,其模态曲率损伤因子变化特征不明显而不容易区分开来,这也说明模态曲率损伤因子有一定的适用范围,对较小损伤识别不敏感。
3.3 不同损伤位置的复合材料损伤指标的变化
3.3.1 模态固有频率的变化
选取了不同位置处含相同大小损伤的层压板,损伤位置分别为A、B、C,分别对应层压板的左、中、右三处位置。针对不同损伤位置的情况,选取各层相同的40mm×40mm 的损伤面积,分别考虑其模态固有频率变化率和模态曲率损伤因子的变化情况。
不同损伤位置的模态固有频率变化率如图8所示。从图8可看出,随着损伤位置的变化,模态频率即材料的固有频率变化率也发生了变化;对于损伤情况相同铺层不同的复合材料,随着损伤位置的右移,10阶固有频率变化率也随之增大;但固有频率变化率都在10阶、12阶处具有较大的变化率,具有一致性。这对于损伤的发现和检测具有指导意义。

图8 不同损伤位置的模态固有频率变化率
3.3.2 模态曲率损伤因子的变化
不同损伤位置的模态曲率损伤因子如图9 所示。从图9可看出,随着损伤位置的向右移动,模态曲率损伤因子确定的损伤位置也随之由测点10 转向测点8再转移到测点6,比较准确地识别了损伤位置的变化。证明模态曲率损伤因子不仅可给出损伤程度,并且可以准确地识别出损伤所在的位置,故可以作为损伤位置的识别参数。
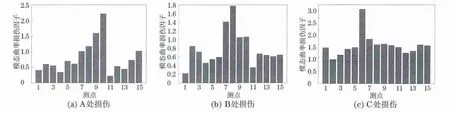
图9 不同损伤位置的模态曲率损伤因子
4 结语
(1)通过引入典型的低速冲击分层损伤模式和粘结单元,模拟了冲击后含分层损伤的复合材料层压板的振动模态特性。通过改变损伤程度、损伤位置、材料铺层,可以看出模态固有频率变化率在不同阶的变化的差异性,以及其在不同阶的变化的一致性;表明选择合适阶的变化率可以作为损伤出现的指标,有利于损伤的发现。
(2)在原有模态曲率基础上,采用改进的模态曲率损伤因子作为损伤指标识别损伤,更加完整准确地描述了损伤信息。随着损伤程度的增大,模态曲率损伤因子也随之增大,其对损伤识别的灵敏度增加;铺层信息对于模态曲率损伤因子的识别也有一定影响;模态曲率损伤因子能比较准确地给出损伤位置的变化。
[1]DOEBIING S W,FARRAR C R,PRIME M B.Asum-rnary review of vibration based damage identification methods[J].The Shock and Vibration Digest,1998,30(2):91-96.
[2]CARDEN E P.Vibration based condition monitoring:a review[J].Struct Health Monit,2004(3):355-377.
[3]ZOU Y,TONG L,STEVEN G P.Vibration-based model-dependent damage(delamination)identification and health monitoring for composite structures:a review[J].J Sound Vib,2000(2):357-378.
[4]DELLA C N,SHU D.Vibration of delaminated composite laminates:a review[J].Appl Mech Rev,2007(60):1-20.
[5]PIERRE V,VLADIMIR B,PATRICK T.Prediction of the propagation of impact-induced delamination in carbon/epoxy laminates[J].Composite Structures,2013(95):227-235.
[6]朱炜垚,许希武.T300/QY8911层合板低速冲击试验及有限元模拟[J].材料科学与工程学报,2013,31(1):68-73.
[7]李德葆,陆秋海.实验模态分析及其应用[M].北京:科学技术出版社,2001.

