城市轨道交通车辆走行部维修周期优化模型

孙 超徐永能

（1.北京轨道交通路网管理有限公司，100101，北京；2.南京理工大学交通工程系，210094，南京∥第一作者，硕士）

城市轨道交通车辆走行部维修周期优化模型

孙 超1徐永能2

（1.北京轨道交通路网管理有限公司，100101，北京；2.南京理工大学交通工程系，210094，南京∥第一作者，硕士）

阐述了国内外轨道车辆设备的维修模式。针对现行设备维修模式的不足，在已有研究的基础上提出了容许量的概念，并建立了基于可靠度的最佳维修周期优化模型。模型融合了故障发生等级、故障发生频率和可靠度函数等信息。以国内某地铁车辆的故障数据为例，计算车辆走行部的转向架、制动系统、辅助系统等相关系统在优化模型下的最佳维修周期，提出了单系统“隔双周检”和“隔10日检”、多系统“隔10日检”的维修模式。

城市轨道交通；车辆维修；可靠性分析；维修周期优化

First-author's addressBeijing Metro Network Control Center，100101，Beijing，China

对于城市轨道交通车辆设备的维修，在长期的实践中形成了预防维修和事后维修两大类［1］。预防维修可分为定期维修和状态维修两种方式。在状态修的基础上，上海地铁又提出了均衡修的概念，充分利用车辆运营高峰回库的窗口时间，提高车辆利用率。法国巴黎地铁和日本地铁均根据预防维修的原则，从走行公里与运行时间上考虑对车辆的各部件进行修理。我国深圳地铁和京港地铁等则根据车辆运行公里采用预防维修，实际进行维修时往往以里程数和日历数先到为准［2］。

采用预防维修，会在不同程度上出现维修过剩或维修不足的现象，并且维修作业过程占用过多的运营时间，导致车辆利用率降低。另外，按照传统维修的观念，定期维修能够避免故障的发生，有时能改变故障的后果；但按照RCM（以可靠性为中心维修）的观念，采用定期维修难以避免故障的发生，不能改变故障发生的后果［3-4］。事后维修是故障发生后进行被动修理，它虽然避免了预防维修可能出现的维修过剩，但若发生故障则损失难以估计。

针对不同维修模式中出现的问题，本文提出了基于可靠度的最佳维修周期的确定方法。其核心思想是：对设备在使用期发生的故障进行分析，明确设备可靠度的变化趋势。该方法根据各故障发生的后果，确定可接受的最低可靠度下对应的维修周期，从而将维修模式问题转化为可靠度约束条件下求解最长维修周期的单目标优化问题。本文所提出的求解方法较为简便，避免了过于复杂的数学模型和算法，提高了计算效率，保证了计算的准确度，在实际工程中具有较强的操作性。

1 最佳维修周期的优化模型

1.1 综合框架

1.1.1 维修策略描述与故障等级划分

由于设备和运行情况的多样性，使得维修策略和故障数据具有多种方式和来源，因此，需要对使用的维修策略和故障数据进行说明，然后根据海因里希法则对故障等级进行划分。

1.1.2 最佳维修周期确定

首先，基于故障等级划分原则与故障统计数据确定设备当量A类故障的历史可靠度；然后，根据可靠性寿命试验理论对故障统计数据进行处理，确定该设备的可靠度函数，得到可靠寿命与可靠度表；最后，根据最佳维修周期优化模型确定单系统和多系统的维修周期。

1.1.3 分析验证

将提出的维修模式与现行的维修模式进行比较，计算该设备在新维修模式下的可靠度增加值及维修周期的延长时间等参数，验证所提维修模式的有效性。

1.2 轨道交通车辆维修策略描述

1.2.1 维修策略说明

预防维修中采用的维修策略基本分为更换、修理和保养三类［5］。更换是指将损坏的设备进行拆除，换上全新的备品备件。这种方法常用于设备故障较为严重、修理产生的成本大于更换成本的情况下。根据维修理论，为简化模型和方便研究，采用更换的方式进行维修后，可以将设备视为全新的、性能完全相同的设备［6］，设备的故障间隔时间服从独立同分布。

1.2.2 可靠性理论基础

单元系统的可靠度是指设备在规定的时间内和规定的条件下，完成规定功能的概率。可靠度是时间的函数，一般记为R（t），称为可靠度函数。

式中：

R（t）——样本在t时刻能正常工作的概率；

N——样本量；

n（t）——在t时刻失效的样本量。

平均寿命（tMTBF）表示设备的无故障工作时间。采用本文的维修策略，对于可修产品，其寿命指相邻两次故障间的故障时间。平均寿命即为平均故障间隔。

式中：

ni——第i个设备的故障次数；

tij——第i个设备从第j-1次故障到第j次故障的工作时间。

1.3 海因里希法则

对故障等级进行量化时，使用海因里希法则。海因里希法则是美国著名安全工程师海因里希提出的300∶29∶1法则［7］。在进行可靠性分析前，按照海因里希法则，将走行部相关系统发生的故障划分为A、B、C三类故障。故障等级的划分原则如表1所示。

表1 故障等级划分原则

1.4 维修周期的优化模型

1.4.1 单系统最佳维修周期的确定

历史可靠度（R）是指设备在统计期内完成规定功能，而没有发生C类及以上故障的概率。其计算式为：

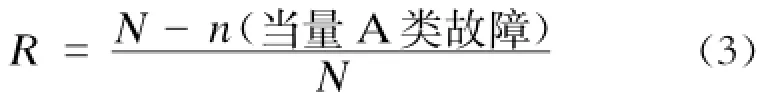
复杂设备的故障具有多样性，在进行可靠性分析时，需要将发生的各类故障进行归一。根据海因里希法则，各类故障等级与转化准则如表2所示。

表2 故障等级与转化准则

容许量r是指工程实际可以接受的设备或系统的最低可靠度。本文将容许量设为设备或系统的历史可靠度。即：

若设备的可靠度Ri对应的可靠寿命为ti，i= 1，2，…，n，则根据可靠度函数有：

式中：

f（ti）——单系统的故障概率密度函数。

当Ri=r时，设ti=a，则有：

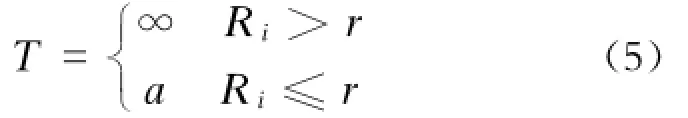
式中：

T——单系统的最佳维修周期。

1.4.2 多系统最佳维修周期的确定

可靠性框图是为预计或估算产品的可靠性所建立的方框图，是系统各部分及其可靠性意义下连接关系的图形表达，表示各部分的正常或失效状态对系统状态的影响［8］。采用可靠性框图法分析列车系统的可靠性模型，可以得出列车系统是一个串联系统［9］。基于此，轨道交通车辆走行部相关系统的可靠性框图如图1所示。

图1 轨道车辆走行部结构可靠性框图

由图1得到轨道交通车辆多系统的可靠性模型：

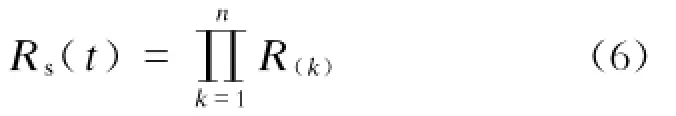
式中：

R（k）——设备k的历史可靠度；

Rs（t）——车辆多系统历史可靠度。

设rs（t）为轨道交通车辆多系统的容许量，则有：

若设备k的可靠度Ri，（k）对应的可靠寿命为ti，（k），k=1，2，…，n，则有：

式中：

Rsi（t）——车辆多系统的可靠度。

当Ri，（k）=R（k）时，设ti，（k）=a（k），则多系统维修周期T（k）的数学模型为：

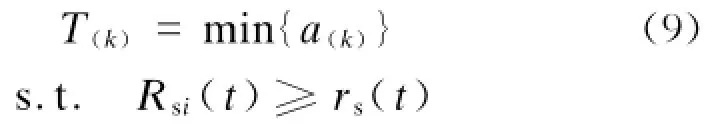
2 实例分析

2.1 走行部相关系统维修策略

本文采用国内某地铁车辆设备2010—2012年的统计故障数据，将其中4列车作为样本进行数据分析。目前，该地铁的车辆设备采用隔日检、全效修、架修和大修相结合的维修制度。隔日检是指以3 d为一周期对车辆的重要部位进行的检查。

车辆走行部相关系统指转向架、制动系统以及辅助系统。基于统计的故障数据，转向架故障主要发生在轮对踏面、润滑器以及悬挂系统。制动系统的故障主要发生在制动控制模块、供风单元等。辅助系统发生的故障主要由车头灯、普通照明及蓄电池等的故障组成。可以看出，走行部相关系统的维修策略基本以更换为主。因此，可靠性特征量可由式（1）和式（2）求得。

2.2 故障等级划分

基于海因里希法则分析该地铁车辆设备故障。根据故障等级的划分原则，将转向架、制动系统及辅助系统的常见故障进行等级划分，结果如表3所示。

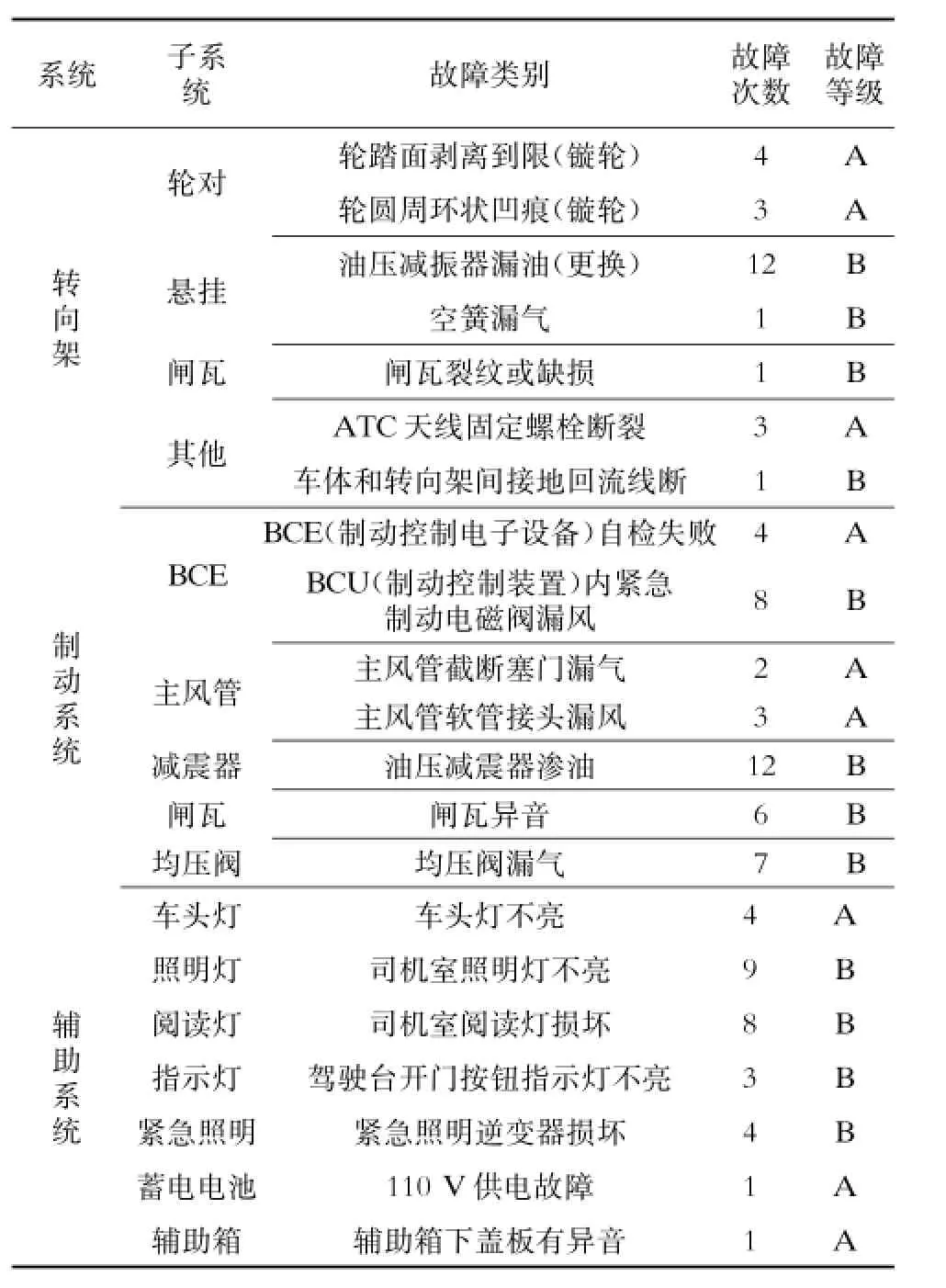
表3 故障等级划分表

2.3 单系统最佳维修周期的确定

首先，对发生的故障数据进行总体描述统计，并计算历史可靠度和容许量；然后，通过统计量检验，确定单系统寿命分布和可靠度函数；最后，确定单系统最佳维修周期。由于方法类似，本节详细给出转向架的故障描述统计表、拟合度检验表以及可靠度-时间关系图，制动系统和辅助系统直接给出历史可靠度、和寿命分布。

2.3.1 转向架最佳维修周期的确定

对转向架的故障间隔观测值进行汇总，将t（d）∈［10，93］分为8组，统计结果如表4所示。从表4中可以看出，转向架故障在［10，20］的区间内发生的频率最高。

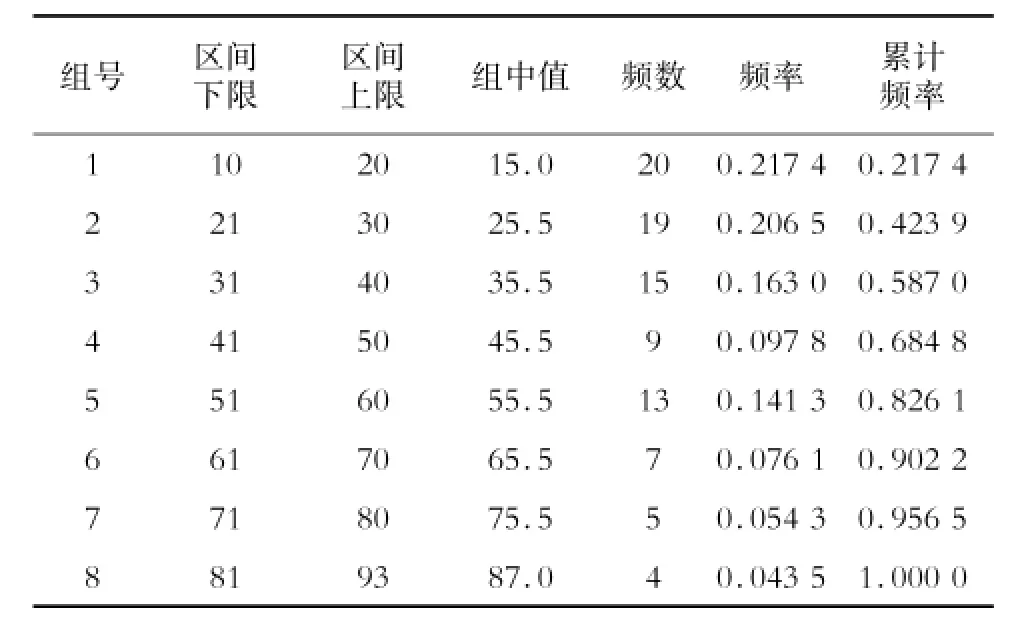
表4 转向架故障频率及累积频率

由表3及表4可知，统计期内，转向架共发生故障92次。其中，发生A类故障10次，B类故障15次，C类故障67次。则n（当量A类故障）=10+根据式（3），可计算出转向架当量A类故障的历史可靠度：

由式（4）得r=0.883。

将转向架的故障间隔时间导入Weibull++7软件，采用极大似然估计法对正态分布、对数正态分布、Weibull分布进行参数估计和拟合度检验。其中Weibull分布最早在1939年由瑞典物理学家威布尔提出［10］，并迅速发展成为可靠性工程中重要的分布类型。计算得到的参数值如表5所示。

表5 转向架寿命分布模型

由表5可知，转向架故障数据正态分布的P值小于显著性水平0.05，因此其只服从对数正态分布和Weibull分布。其中，3P-Weibull分布的K-S统计量最小，因此转向架的故障数据最符合3PWeibull分布。

转向架可靠度函数R（t）=e-0.006×（t-6.975）1.456， tMTBF=39.16 d。转向架可靠度随时间的变化如图2所示。

根据转向架的可靠度函数，可以得到转向架可靠寿命所对应的关键可靠度，如表6所示。

从表6中可以看出，转向架可靠寿命ti∈［9.4，19.6］，可靠度Ri∈［0.80，0.98］。因为r= 0.883，根据单系统最佳维修周期的确定法则得T= 15.4 d。即最长维修周期优化为15.4 d时，转向架的可靠度仍高于隔日检维修模式所得到的可靠度。因此，转向架可采取“隔双周检”的维修模式。

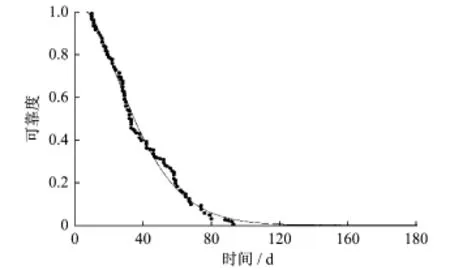
图2 转向架可靠度-时间关系图

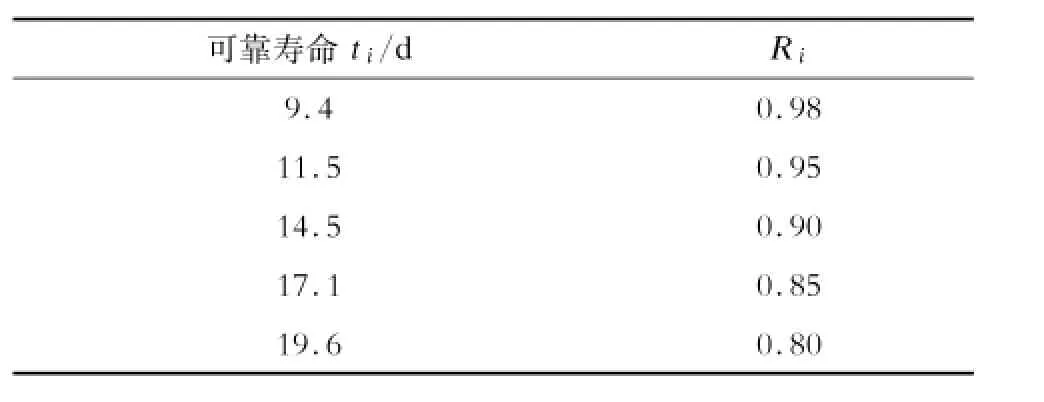
表6 转向架可靠寿命与可靠度表

2.3.2 制动系统和辅助系统最佳维修周期的确定

制动系统和辅助系统最佳维修周期的确定方法同转向架。采用类似于转向架历史可靠度的计算方法，可得制动系统的历史可靠度为85.93%，辅助系统的历史可靠度为87.44%。根据式（4），得到制动系统的r为0.859，辅助系统的r为0.874。

根据转向架可靠度函数的建模方法，得到制动系统与辅助系统的寿命分布均最符合3P-Weibull分布，可靠度函数分别为R（t）=e-0.028×（t-9.600）1.048，R（t）=e-0.060×（t-9.725）0.872；tMTBF分别为39.35 d和36.88 d。

根据制动系统和辅助系统的可靠度函数，可以得到制动系统和辅助系统可靠寿命所对应的关键可靠度，如表7和表8所示。

表7 制动系统可靠寿命与可靠度表

表8 辅助系统可靠寿命与可靠度表

由表7可知，制动系统可靠寿命ti∈［10.3 16.8］，可靠度Ri∈［0.80，0.98］。因为r=0.859，根据单系统最佳维修周期的确定法则，可得T= 14.6 d。即制动系统可以采取“隔双周检”的维修模式。

由表8可以看出，辅助系统可靠寿命ti∈［10.0 14.2］，可靠度Ri∈［0.80，0.98］。因为r =0.874，根据单系统最佳维修周期的确定法则，可得T=12.2 d。即辅助系统可以采取“隔10日检”的维修制度。

2.4 多系统最佳维修周期的确定

在确定多系统最佳维修周期时，将走行部的转向架、制动系统和辅助系统作为串联系统。由式（6）计算得到走行部的历史可靠度Rs（t）=66.55%。根据式（7），走行部的容许量rs（t）=0.666。

将走行部各相关系统的关键可靠度与对应的维修周期进行关联，可得到走行部可靠度变化趋势，如表9所示。

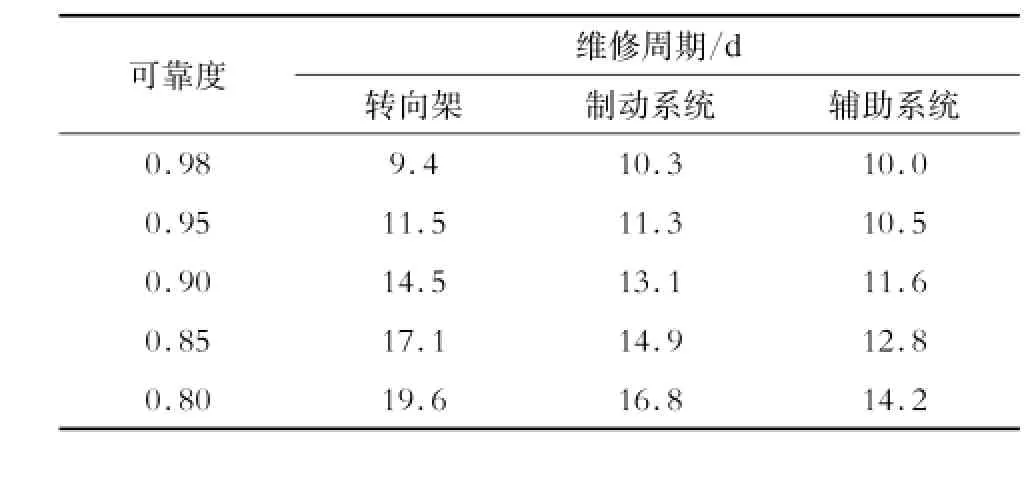
表9 走行部可靠度变化趋势

根据多系统最佳维修周期的确定法则，可得T（k）=12.2 d。如果考虑适度安全的原则，可以将维修周期选择在10～11 d，走行部可靠度高于0.81；如果考虑严格安全的原则，建议将维修周期选择为10 d，走行部可靠度高于0.91。

3 结语

通过分析城市轨道交通车辆设备历史故障数据，对单系统提出了“隔双周检”与“隔10日检”维修模式；对多系统提出了“隔10日检”的维修模式。相比国内某地铁现行的“隔日检”维修模式，本文提出的维修模式延长了维修周期，优化了资源配置，提高了车辆的维修效率和车辆的利用率。在本文提出的维修模式下，转向架、制动系统与辅助系统的可靠度均高于0.90，可以认为最多仅会发生10%的当量A类故障。下一步将结合表3中给出的车辆设备常见故障，进行故障模式影响及危害性分析（FMECA），以判断故障对城市轨道交通车辆设备造成的影响，并对优化后的维修周期的可行性进行进一步论证。

［1］ 刘林祥，姚家瑞.现代设备管理［M］.上海：上海科学普及出版社，1989.

［2］ 南京理工大学交通工程系，南京地下铁道有限责任公司运营公司.南京地铁车辆创新型维修模式研究中期评估报告［R］.南京：南京理工大学，2012.

［3］ 张红蓉.兰州石化公司设备可靠性管理研究［D］.天津：天津大学，2009.

［4］ 贾希胜.以可靠性为中心的维修决策模型［M］.北京：国防工业出版社，2007.

［5］ 金玉兰.生产系统有限时间区间弹性周期预防性维修策略研究［D］.上海：上海交通大学，2009.

［6］ 安志萍，赵丽萍，敖琼.构建预防性维修年龄维修策略模型［J］.设备维修，2007，22（8）：35.

［7］ 习徐红.海因里希法则与有效控制事故［J］.广东安全生产，2008（17）：42.

［8］ 贾东梨.基于可靠性框图的配电网接线模式薄弱环节研究［D］.天津：天津大学，2008.

［9］ 张安.地铁车辆的可靠性分配和可靠性预计［J］，质量与可靠性，2006（7）：13.

［10］ 叶慈南，曹伟丽.应用数理统计［M］.北京：机械工业出版社，2007.

Optimum Maintenance Circle Model for Rail Transit Vehicle′s Running Gear

Sun Chao，Xu Yongneng

Some maintainence models on rail transit vehicles in the world are described.According to the deficiency of traditional maintain models，the conception of tolerance is proposed，an optimum maintainence circle model for rail transit vehicle′s running gear systems based on the reliability analysis is presented.The model consists of the information of fault levels，the frequency of fault and reliability function.Based on the fault data from a domestic vehicle depot，the best maintenance circle for bogie，brake and the supporting system of vehicle is calculated，including the biweekly check for single system，10 days interval check for both the single and the multiple systems.

urban rail transit；vehicle maintenance；reliability analysis；maintenance circle optimization

U 279.1：U 270.33

10.16037/j.1007-869x.2015.01.019

2013-05-08）