DFIG型风电机组多点接入地区电网暂态稳定分析

詹孝和，徐永卫，朱梅

(1.江苏华电扬州发电有限公司，江苏 扬州 225000；2.扬州供电公司，江苏 扬州 225009)

DFIG型风电机组多点接入地区电网暂态稳定分析

詹孝和1，徐永卫2，朱梅2

(1.江苏华电扬州发电有限公司，江苏 扬州 225000；2.扬州供电公司，江苏 扬州 225009)

大型风电场集中并入电网，改变了原有电网的潮流分布﹑电压水平和系统惯量，给电网稳定性造成较大影响。本文建立了双馈直驱风力发电机的通用模型，选用牛顿—拉夫逊法(功率式)计算电力系统潮流，在接入同步水电机组和双馈风电机组﹑单点和多点接入﹑不同接入点﹑不同接入容量等情况下，分析系统潮流和暂态稳定性能，以各种情况下的故障临界清除时间，对比分析含风电场的电网的暂态稳定性。

双馈直驱风力发电机；并网；潮流分析；暂态稳定

0 引言

20世纪90年代，世界各国为了应对全球性的能源危机和温室效应，加强了对可再生能源的开发利用，这给风能等清洁能源带来了发展的契机。风电作为新能源发电的主角之一，已成为驱动新能源发电发展的不二选择，也是目前国内外新能源发电的研究重点[1]。因此，在风电建设与接入电网之前，进行必要的包含风电的电力系统分析计算，研究风电接入后系统运行的稳定性变化情况，无论是对于业主还是电网部门而言，都是非常必要的。一方面有助于发现风电并网后电力系统中可能出现的问题，明确风电接入对于系统稳定性的影响；另一方面，通过必要的改善措施增强风电并网后电网的安全性与稳定性，最大限度地保证风电的并网发电，保障业主投资的回收与利益。

随着风电机组技术的进步及风电在电网中所占比例的迅速提高，目前多个国家的风电并网导则都对风电场提出了更高的要求：在规定的故障及电网电压跌落期间，保证一定时间范围内风电场能够连续运行而不脱离电网，要求风电场在电网故障发生后发出无功功率参与电网的电压控制[2]。例如从2003年开始，德国E.on电网公司除了要求故障后电网电压恢复期间风电场必须保持并网运行外，还要求风电机组动态发出无功功率以支持电网电压，防止风电机组由于电压过低导致的跳闸。风电场的这种故障期间保持并网不间断运行的能力通常称为风电场的“低电压穿越能力”。

本文重点研究双馈感应电机的结构﹑模型﹑基本工作原理和优点等，研究分析风电系统的并网模型，采用实际地区电网的数据，在不同的情况对大规模风电集中接入后的电网暂态稳定性进行分析，并给出相应的结论和建议。

1 双馈感应发电机的数学模型

双馈型发电机(Doubly-fed Induction Generator，简称DFIG)是绕线式异步发电机的一种，其定子绕组直接接入工频电网，转子绕组接线端由三只滑环引出，因此可以对转子进行交流励磁。其转子绕组通常由一台双向变频器接至电网，图1为其结构原理图。

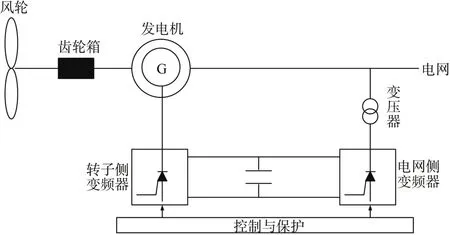
图1 双馈型风机结构原理图Fig.1 Structure schematic diagram of DFIG

由图1可知，双馈风力发电系统的主要部件包括风轮﹑增速齿轮箱﹑交流发电机﹑双PWM变流电路﹑控制系统等。风力机把风能转换为机械能，发电机把机械能转换为电能。双馈感应风力发电系统的工作原理是：当风速降低时，风力发电机转速降低，双馈感应发电机的转子转速ω也降低，转子绕组电流产生的旋转磁场转速ω2低于双馈感应风力发电机的同步转速ω1，定子绕组感应电动势的频率f低于额定频率f0(50Hz)，此时转速测量装置立即将转速降低，这一信号反馈到交流-直流-交流双向变频器，使转子电流频率增高，则转子旋转磁场的转速又回到同步转速ω1，于是定子绕组感应电动势的频率又恢复到额定频率f0[3]。以同步旋转坐标系为参考，采用定子磁链进行定向，根据双馈机的电压及磁链方程可得定子侧电功率为[4]

转子侧电功率为

式(1)-(3)中：usd、usq为定子d轴﹑q轴电压；urd、urq为转子d轴﹑q轴电压；isd﹑isq为定子d轴﹑q轴电流；ird﹑irq为转子d轴﹑q轴电流；Ps﹑Qs为定子侧有功和无功功率；Pr﹑Qr为转子侧有功和无功功率。

2 风电并网潮流分析

潮流计算是根据给定的电网结构﹑参数和发电机﹑负荷等元件的运行条件，确定电力系统各部分稳态运行状态参数的计算。通常给定的运行条件有系统中各电源和负荷点的功率﹑枢纽点电压﹑平衡点的电压和相位角。待求的运行状态参量包括电网各母线节点的电压幅值和相角，以及各支路的功率分布﹑网络的功率损耗等。

本文选择的是牛顿法(功率式)[5]，将发电机节点视为PV节点，n个节点电力系统的潮流方程的一般形式是

采用直角坐标时，节点电压可表示为

导纳矩阵元素则表示为

将上述表示式代入式(4)的右端，展开并分出实部和虚部，便得

假定系统中的第1,2,…,m号节点为PQ节点，第i个节点的给定功率设为Pis和Qis，对该节点可列写方程是2(n-1)个。不难写出如下的修正方程式

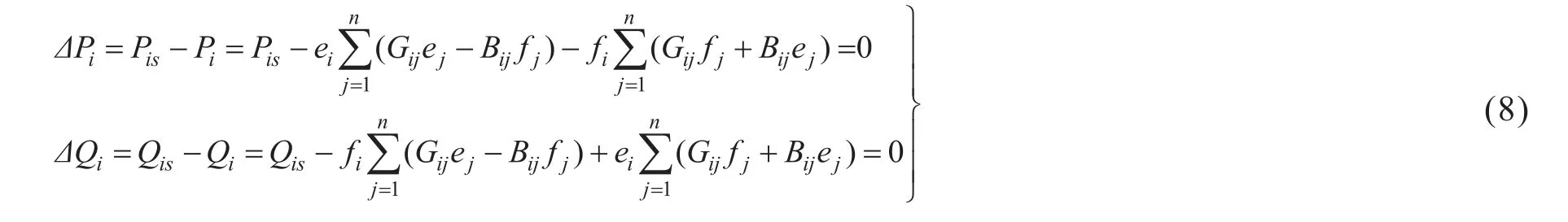
假定系统中第m+1，m+2，…，n-1号节点为PV节点，则对其中每一个节点可以列写方程

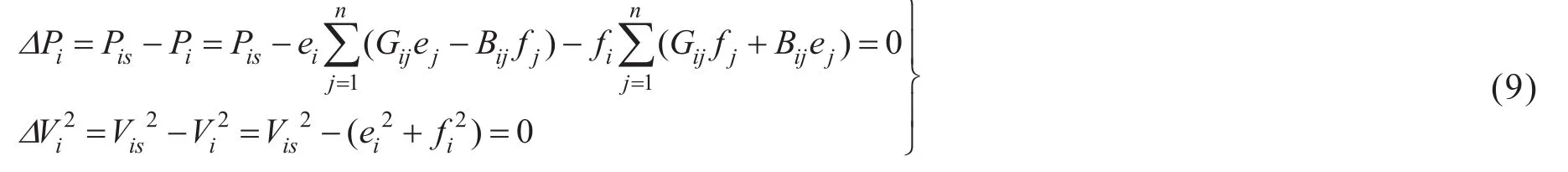
第n号节点为平衡节点，其电压Vn＝en+jfn是给定的，故不参加迭代。

式(8)和式(9)总共包含了2(n-1)个方程，待求的变量有e1，f1，e2，f2，…，en-1，fn-1，也是2(n-1) 个。不难写出如下的修正方程式

式中：J是雅可比矩阵。

上述方程中雅可比矩阵的各元素，可以对式(8)和式(9)求偏导数获得[6]。当i≠j时

3 风电并网暂态稳定分析

3.1 电网暂态稳定分析概况

电力系统暂态稳定指的是电力系统受到大干扰后，各发电机保持同步运行并过渡到新的或恢复到原来稳定运行状态的能力，通常指第一或第二摆不失步[7,8]。电力系统暂态稳定分析的主要目的是检查系统在大扰动下(如故障﹑切机﹑切负荷﹑重合闸操作等情况)，各发电机组能否保持同步运行。如果能保持同步运行，并且有可以接受的电压或频率水平，则称此系统在这一大扰动下是暂态稳定的。

常规电力系统暂态稳定裕度常用故障临界清除时间(Critical Clearing Time, CCT)衡量，CCT也适用于含有风电的电力系统暂态稳定分析。采用故障临界清除时间表征电网暂态稳定性：线路故障临界清除时间越大，系统的暂态稳定性越强。系统故障取线路短路最严重情况，即线路三相短路。CCT表示为：

式中：tf和tcl分别是故障发生和清除时间。

3.2 双馈风电机组的暂态特性

DFIG是在普通绕线式异步感应电机的基础上，外加连接在转子滑环与定子之间的变流器及其控制系统，属于交流励磁异步化同步电机的一种[9]。转子的电角速度ωr﹑转子外加励磁电源产生的旋转磁场角速度ωe与同步旋转磁场角速度ω0的关系为：

DFIG为异步运行，其转子转速可以通过改变交流励磁电源的频率进行调节，克服了传统同步发电机必须严格同步的要求，把发电机机械与电气之间的刚性联系变为柔性联系[7]。其稳态电路模型如图2。

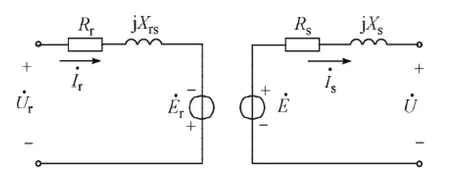
图2 DFIG的稳态电路模型Fig.2 Steady state circuit model of DFIG

DFIG具有广泛的稳定运行范围，在任一滑差的运行点上具有与传统同步发电机相同的功角特性：

4 算例分析

4.1 基础数据

QYS风电场被列为全国十大风场之一，同时也是所属省份全省最大的风电场，根据LC气象站及风电场场址区测风资料统计，气象站的多年平均风速为1.57m/s(1975年～2004年)，风电场场址区10m高度测风年(2003年2月1日～2004年1月31日)年平均风速为5.49m/s，最大风速25.2m/s。其主导风向稳定，风速的日变化较小，破坏性风速少，大风日多且持续时间长，具有一定的风资源开发前景。因此本论文选取ESLC地区的大规模风电资源并入电网为例进行研究。

4.2 故障临界清除时间

为了研究地区电网与风电场的暂态稳定性，本文中故障设置为风电场升压站110kV母线发生三相短路，这是风电场有可能遭遇的最恶劣情况。以NP110kV并网母线为例，接入规划容量(491.3MW)风电计算水平下，故障类型为NP110kV母线发生三相短路，故障开始时间为tf＝5s，故障清除时间分别为tcl＝5.39s和tcl＝5.40s时，仿真分析NP110kV母线的电压变化情况。

由图4可以看出，在故障清除时间CT(clearing time)为0.39s时，NP110kV母线电压仍可恢复到正常水平，而当CT=0.40s，母线电压大幅度振荡，不可恢复至正常水平，系统崩溃，表明ENP110kV母线发生三相短路时，系统的故障临界清除时间(CCT)为0.39s。

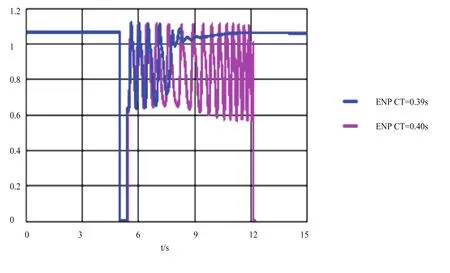
图4 ENP110kV母线发生故障时电压变化曲线Fig.4 Voltage curve of ENP 110kV bus after fault

4.3 风电场单点接入暂态特性分析

通过对包含风电场动态模型的时域仿真，求解风电场单点接入时，电网暂态故障条件下系统的故障临界清除时间，判断风电场对系统暂态稳定的影响。风电场单点并网时，考虑并网点网架结构和并网容量的典型性，仅考虑母线ENP110接入风电场(见表1)，计算在接入与不接入这2座风电场时的CCT，故障点设置在NP110kV母线，故障类型为三相短路，故障开始时间tf＝5s。

由表1可以看出，在风机并网点发生三相短路时，接入风机与未接风机的CCT基本相等。这是由于当在风机并网点三相短路时，由于其母线电压跌落为零，风机脱网，对网侧无贡献[22]，故在接入风机与未接风机时，CCT基本相等。从图5可以看出，NP110kV母线并网容量98.8MW时，在接入与不接入风电场，故障清除后恢复过程基本相同，风电机组的贡献微弱。

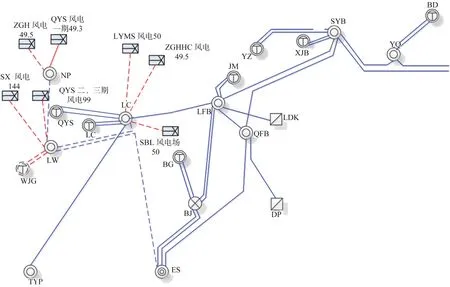
图3 风电接入地理位置接线图Fig.3 Location of Wind generation access to the power grid

表1 风机接入后系统故障CCT对比表(单位：s)Tab.1 CCT of fault after wind generation access to the power system

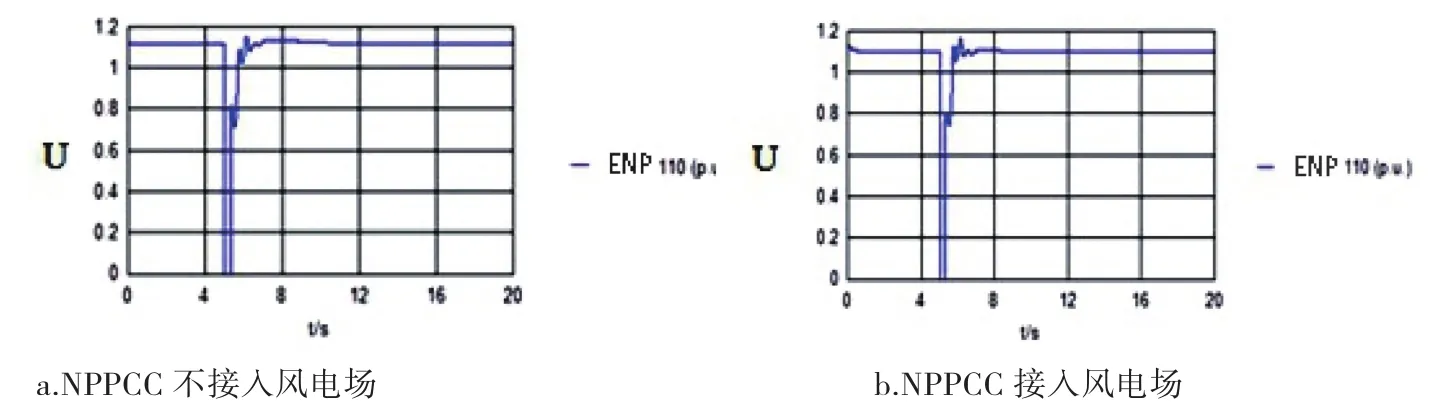
图5 风机并网母线电压变化曲线Fig.5 Connection bus voltage curve of wind generation

4.4 风电场多点接入暂态特性分析

方案1：NP﹑LC﹑LW110kV母线接入规划风电机组时，在NP110kV母线处发生三相短路，故障开始时间tf＝5s，故障清除时间tcl＝5.33s，以SBL风电场为例观察双馈机组各状态量变化(以下各值均为标幺值)。

方案2：NP﹑LC﹑LW110kV母线接入同等容量的同步机组小水电机组时，NP110kV母线处发生三相短路，故障开始时间tf＝5s，tcl＝5.33s，选择替代SBL风电场位置的水电机组为例，观察各状态量变化(以下各值均为标幺值)。

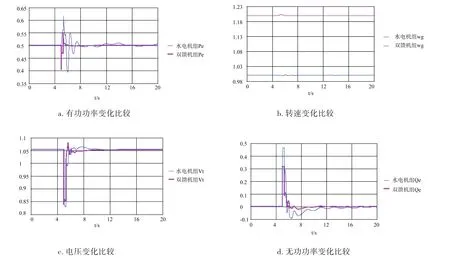
图6 双馈机组与同步机组各状态变量的对比曲线Fig.6 Comparison curves fo DFIG and Synchronous generator

图a和b的对比分析得出，用同等容量的水电机组代替风力发电机组，在发生同样的故障且故障同时清除的条件下，同步机组与双馈风电机组都会加速并发生转速及有功功率的振荡，双馈电机风电场有功功率振荡相比同步机组电厂的有功功率振荡要小很多，这充分反映出电网侧发生故障时双馈风电机组与同步机组不同的特性，双馈风电机组较同步机组有着更好的暂态稳定特性。

图c﹑图d可以看出，用同等容量的水电机组代替风力发电机组，在发生同样的故障且故障同时清除的条件下，双馈机组的电压和无功功率变化在故障清除后恢复得更快，其对电网的支撑作用也明显高于水电机组。

从能量平衡角度看，在系统故障期间，由于电磁转矩和机械转矩不平衡，会导致双馈风电机组加速，其中一部分不平衡能量会暂存在风电机组叶片与转子加速旋转的动能中，这部分暂存的能量能够降低风电机组在暂态过程中对电网的冲击[25]。因此，在一定的并网容量下，接入双馈风电机组时，电力系统的暂态稳定性要好于在同一点接入等容量同步发电机组。

5 结论

本文研究了双馈风电机组的数学模型，对其并网后的潮流计算进行了分析，在此基础上分析了风电机组的暂态数学模型，通过实际地区电网的仿真分析，验证在多点接入情况下电网的暂态稳定能力，得到以下结论：(1)双馈风电机组较同步机组有着更好的暂态稳定特性。在发生同样的故障且故障同时清除的条件下，双馈机组的电压和无功功率变化在故障清除后恢复得更快，其对电网的支撑作用也明显高于同步发电机组。(2)在风机并网点发生三相短路时，接入少量风机与未接风机的CCT基本相等。(3)在接入容量一定的情况时，故障清除后，接入风机比不接入风机母线电压恢复得更为平稳，风电场接入后对电网的暂态稳定性有明显的改善，并且随着系统并网风电容量的增加，系统的暂态稳定性不断提高。

[1] 魏巍, 王渝红, 李兴源, 等.基于PSASP的双馈风电场建模及接入电网仿真[J].电力自动化设备, 2009, 29(12):68-73.Wei Wei, Wang Yuhong, Li Xingyuan, et al.Large wind farm modeling and grid-connection simulation based on PSASP.Electric Power Automation Equipment, 2009, 29(12):68-73.

[2] 肖伸平, 曾钰, 赵培哲.改进干扰观测法在光伏发电系统 MPPT 中的应用[J].新型工业化, 2014, 4(4):45-50.XIAO Shen-ping, ZENG Yu, ZHAO Pei-zhe.An Improved Perturbation and Observation Method for Photovoltaic Power Generation System[J].The Journal of New Industrialization, 2014, 4(4):45-50.

[3] Zhang Feng, Li Mingxia1, Fan Guowei, Luo Zhongyou, Chang Xiqiang.Impact of Wind Integration on Transient Voltage Stability in Regional Grid[J].Electricity, 2012, (2):20-25.

[4] Ekanayake J B, Holdworth L, Wu X G.Dynamic Modeling of Doubly Fed Induction Generator Wind Turbines[J].Power Systems, 2003, 2(18):803-809.

[5] 崔强, 王秀丽, 唐伦, 等.考虑系统风电接纳的尖峰电价决策研究[J].新型工业化, 2014, 4(4):45-50.CUI Qiang, WANG Xiuli, TANG Lun, et al.Decision Model of Critical Peak Pricing Considering Wind Power to Be Integrated[J].The Journal of New Industrialization, 2014, 4(4):45-50.

[6] 杨琦, 张建华, 李卫国.电力系统接入风电场后的暂态稳定分析[J].高电压技术, 2009, 35(8):2042-2047.YANG Qi, ZHANG Jian-hua, LI Wei-guo.Analysis on Transient Stability of Integration of Wind Farms into Power Systems[J].High Voltage Engineering, 2009, 35(8):2042-2047.

[7] Zhang XueMin, Mei ShengWei, Wu ShengYu.Transient stability and emergency control[J].Science in China(Series E:Technological Sciences), 2009, 52(2):420-428.

[8] 谷雅琼, 于惠钧, 邓栋, 等.基于 MATLAB 的风力发电机组低电压穿越仿真[J].新型工业化, 2014, 4(10):18-22.Gu Yaqiong, Yu Huijun, Deng dong, et al.Wind Turbine Generator Low Voltage Ride Through Based on MATLAB[J].The Journal of New Industrialization, 2014, 4(10):18-22.

Transient Stability Analysis of DFIG Access to Region Power Grid

ZHAN Xiaohe1, XU Yongwei2, ZHU Mei2
(1.Jiangsu Huadian Yangzhou Power Generation Corporation Limited, Yangzhou, 225000, China; 2.Yangzhou Power Supply Company, Yangzhou 225009, China)

Large-scale wind farms integrated with the grid will change Power flow distribution, voltage Profile and system rotate intertie, which results in Profound influence on transient stability of the Power grid.So it is necessary to study the transient stability of Integration of Wind Farms into Power Systems.In this paper, the general model of doubly-fed and direct drive wind turbines in Power System Analysis Soft Package(PSASP) was used, and the Newton-Raphson method stated with power equation was chosen to calculate the load flow.Wind farms were accessed in single point or multi-points, wind farms were accessed in different points and different capacity of wind farms were accessed, Using PSASP to do load flow calculation and transient stability simulation, the Critical Clearing Times(CCT) in different kind of cases were obtained, then analyzing transient stability of the power system

DFIG; access to power grid; power flow analysis; transient stability

詹孝和，徐永卫，朱梅．DFIG型风电机组多点接入地区电网暂态稳定分析[J]．新型工业化，2015，5(5)：25-32

10.3969/j.issn.2095-6649.2015.05.04

:Zhan Xiaohe, Xu Yongwei, Zhu Mei.Transient stability analysis of DFIG access to region power grid [J].The Journal of New Industrialization, 2015, 5(5)∶ 25‒32.

詹孝和(1959-)，男，江苏扬州人，高级技师，主要研究方向：继电保护的研究；徐永卫(1966-)，男，江苏张家港人，工程师，主要研究方向：电力通信方面的研究；朱梅(1971-)，女，江苏扬州人，工程师，主要研究方向：电力系统通信方面的研究。