斜坡面路灯安装间距的优化算法研究及其应用
黄静莱,唐文婷,李 勇,闫兴睿,张 涛
(1. 内江师范学院 数学与信息科学学院,四川 内江 641110;2. 内江师范学院 计算机科学学院,四川 内江 641110)
斜坡面路灯安装间距的优化算法研究及其应用
黄静莱1,唐文婷1,李 勇2,闫兴睿2,张 涛1
(1. 内江师范学院 数学与信息科学学院,四川 内江 641110;2. 内江师范学院 计算机科学学院,四川 内江 641110)
针对斜坡面路灯安装间距选取问题,根据路灯照明原理以及影响路灯安装间距因素之间的关系,分别设计了一盏灯和两盏灯优化数学模型,重点讨论了两盏灯之间的最大安装间距问题,并将模型应用于实际问题,提出了合理的安装改进方案,减少了路灯安装成本,提高了路灯的使用效率,并节省了电能资源。
斜坡面;路灯安装间距;照明原理
路灯作为城市生活的重要组成部分,不仅肩负着城市夜晚照明和交通安全,也扮演着美化城市的重要角色。我国是一个人口大国,随着电器化时代的发展,我国对电力资源的需求量相当大,目前国家正大力提倡环保和节约能源。不少研究者发现路灯过分强调美化功能,既降低了路灯的照明效率也造成了资源的严重浪费,因此对路灯的优化设计及其安装间距的优化成为研究的热点。
高尚[1]研究了两盏路灯优化问题,解决了一排路灯以及街道两边路灯的优化模型;韩蕴等[2]研究了路灯的优化排列方式;王巍等[3]分析了照度均匀度和高度均匀度的问题;文献[4-5]探讨了大学校园内路灯的合理布设及优化算法;文献[6]讨论了基于数学建模的城市路灯优化与节能问题。上述研究工作都是基于地面为水平面情况的,但当实际中遇到斜坡面的情况,若同样按照水平面情况来处理则显然不合理。
本文针对斜坡面路灯安装间距选取问题,分析了水平面和斜坡面的区别,根据路灯照明原理以及影响路灯安装间距因素之间的关系,分别设计了路灯安装最大间距的一盏灯和两盏灯优化数学模型,并将模型应用于实际问题,提出了合理的安装改进方案。
假设以下模型讨论的路灯高度为h,路功率为p。
1 水平面上一盏路灯的优化模型
根据物理学知识,被光线照射的物体的亮度依赖于它与光源之间的距离平方的倒数和光线的投射角度[1]。如图1所示,路灯到A点的光线强度Ⅰ为

其中r为O点到A点的距离。
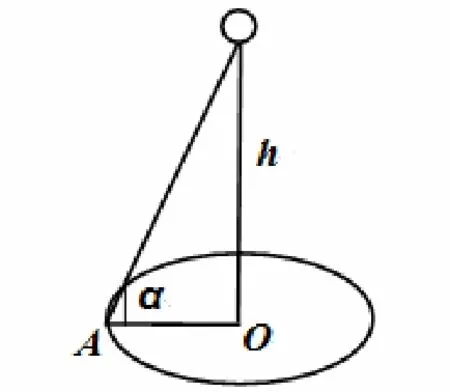
图1 水平面上的一盏路灯
照明强度直接影响可见度,只有照明强度不低于c0(c0通常取2
40w/ m),才能认为物体可见。因此,图1中A点的照明强度cA为

其中α为路灯与A点所在的直线与直线OA的夹角。那么地面上照明强度不低于c0的区域为

时,(5)式无解,地面的物体不可见;当

的区域的物体可见。
2 斜坡面上一盏灯的优化模型
仿照水平面上一盏路灯的可见区域的讨论处理斜坡面上的一盏路灯的可见区域。由于斜坡面使得路灯的照明光线到达地面不能像水平面一样具有对称性(如图2所示),因此,图2中的A点和B点不可能会在同一个照明圆周上,只能分别讨论A点和B点的照明强度。根据物理学知识和式(2)知,要求出这两点的照明强度,需要求出由于斜坡角度而导致的虚拟路灯高度和光照圆周半径。
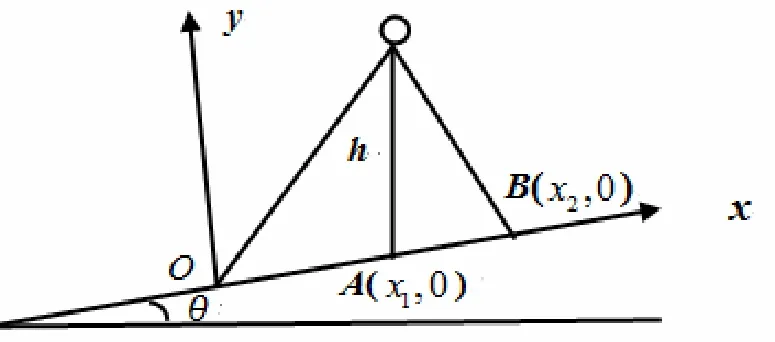
图2 斜坡面上的一盏路灯
设斜坡面的斜度为θ(0≤θ<90°)。如图2所示建立直角坐标系。路灯照射到斜坡面的两交点坐标为A( χ1,0),B( χ2,0)。
构造以A点和B点所在的照明圆周,根据式(2),A点和B点的照明强度cA和cB分别为

照明强度直接影响可见度,只有照明强度不低于c0(c0通常取40w/ m2),才能认为物体可见。因此,取c=min{cA,cB}且满足c≥c0,即可保证路灯的照明效果。例如,根据经验认为cA≤cB,那么为了能够保证路灯的照明效果,必须要求cA≥c0,对(6)式进行放缩有
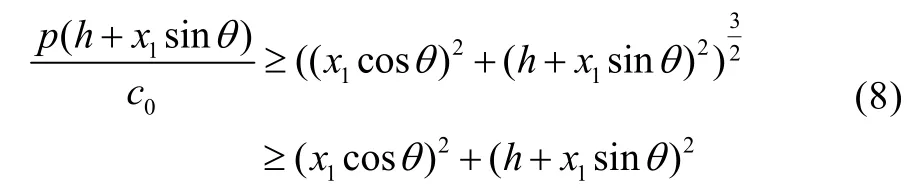
通过对(8)式进行放缩、合并和化解得到,当
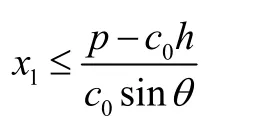
时,能够保证A点的照明效果。
3 斜坡面上两盏路灯的优化模型
路灯通常是以列的方式应用在城市中,两两路灯之间是相互影响的,路灯的间距太长,地面的照明效果不好,路灯的间距太短,造成电能资源的浪费和成本的增加。为了简化问题,尽考虑两盏路灯间距(l)的优化问题,斜坡面的斜度为θ(0≤θ<90°)。设两盏路灯照射到斜面的交点为A,建立直角坐标系如图3所示。B, C两点的坐标为B( χ1,0),C( χ2,0)。
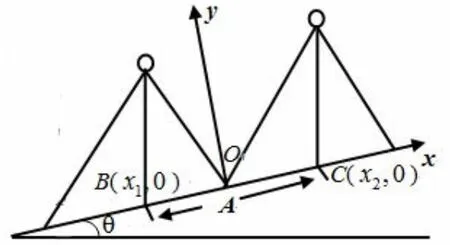
图3 斜坡面上的两盏路灯
根据光强原理,路面上某点的总光线强度等于可以照到该点的所有路灯在该点的光线强度之和,即

其中Ⅰi为第i个路灯照到该点的光线强度。
考虑A点的光线强度,根据(9)式,A点的光线强度等于相邻两盏路灯照到A点的光线强度之和,再根据(6)式和(7)式分别计算两盏路灯照到B点的光线强度cA为
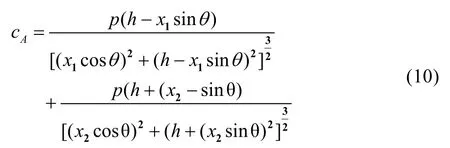
同样,为了保证照明效果,cA必须满足

那么问题转化为在A点的光线强度不低于c0的前提下,使路灯之间的间距尽可能的大,因此,其优化模型为

上述规划问题由于其约束条件(10)式的复杂性使得求解非常困难,在求解中结合了光滑牛顿法[7]和遗传算法的思想[8],利用MATLAB[9]软件得到最优解为

4 实例分析
某高校校内有两段斜面路段,路的两边非均匀地安装着路灯(如图4和图5所示)。路灯选用的是八叉九火玉兰灯(图6所示),为了应用本文路灯间距优化模型检验路灯的安装间距是否合理,假设每盏路灯上灯泡的排列方式不影响光线强度的改变,将每盏路灯的多灯泡功率之和视为一个灯泡的功率。

图4 某高校斜坡面1上路灯

图5 某高校斜坡面2上路灯

图6 某高校八叉九火玉兰灯特写
利用全站仪、棱镜、钢卷尺和经纬仪测得优化模型中所涉及到的参数见表1,其中实测路灯安装距离为路灯的平均间距(路灯之间的间距并不完全相等),所测的数据都只保留小数点后两位有效数字。

表1 斜坡面参数值及结果值
将所测参数代入(13)、(14)式所得结果也列于表1。
从表1可以得到两斜面的最优间距分别为

与实测安装间距比较

(17)和(18)式表明,该高校的两段斜面路灯安装间距过小,没有充分利用此功率路灯的效率,可以适当增加这两段斜面路灯安装间距。
5 结论
研究针对路灯安装间距选取问题,将水平面上路灯安装问题推广到了斜坡面上路灯的安装问题,探究了两者之间的联系和区别,提出了一盏路灯和两盏路灯最优间距的优化模型,并将模型应用于实际问题,并提出了合理的安装改进方案。
[1] 高尚.路灯安置优化问题研究[J].数学的实践与认识,2004, 34(1):1-6.
[2] 韩蕴,张兵.一种城市路灯合理排布的优化设计方法[J].物理学与社会,2007,36(4):331-333.
[3] 王巍,葛爱明,邱鹏,王俊伟,等.基于路面亮度系数表的路灯配光优化及透镜设计[J].照明工程学报,2013,24(2):75-77.
[4] 梁栋,高清平,沈婷婷.大学校园路灯合理布设及优化方法研究[J].中文信息,2013(2):87-88.
[5] 祝洪波.大学校园路灯照明系统的设计探讨[J].现代物业, 2011,10(3):87-88.
[6] 张家昕,仇海全,卢中其.基于数学建模的城市路灯优化与节能研究[J].安徽科技学院学报,2011,25(1):53-55.
[7] 谢亚君,马昌凤.求解非线性规划问题的光滑牛顿法[J].福建师范大学学报(自然科学版),2011,27(5):17-22.
[8] 刘道建,黄天民.序列无约束极小化技术和遗传算法在非线性规划中的应用[J].内江师范学院学报(自然科学版),2002, 17(2):3-6.
[9] 张志涌.精通MATLABR2011a[M].北京:北京航空航天大学出版社,2013.
(责任编辑、校对:赵光峰)
The Research of Streetlights Installation Spacing Optimization Algorithms in the Slope Surface and Its Application
HUANG Jing-lai1, TANG Wen-ting1, LI Yong2, YAN Xing-rui2, ZHANG Tao1
(1. College of Mathematics and Information Science, Neijiang Teachers College, Neijiang 641110, China; 2. College of Computer Science, Neijiang Teachers College, Neijiang 641110, China)
For the streetlights installation spacing in the slope surface selection problem, according to the principle of streetlights and the relationship between the factors influencing the streetlights installation spacing, one streetlight and two streetlights optimization mathematical model are designed respectively. The biggest installation spacing between the two streetlights is discussed, and it is applied to practical problems. The reasonable installation improvement scheme, which reduces the streetlights installation cost, improve the efficiency of the use of streetlights and save the energy resources, is put forward.
slope surface; streetlights installation spacing; lighting principle
O221.2
A
1009-9115(2015)02-0013-03
10.3969/j.issn.1009-9115.2015.02.004
四川省教育厅一般科研项目(12ZB266),数值仿真与数学实验教学示范中心大学生实验项目(0001247)
2014-09-16
黄静莱(1994-),女,新疆乌鲁木齐人,内江师范学院学生。
张涛(1982-),男,四川雅安人,讲师,研究方向为应用数学。

