秩和比法在居民食用碘盐和重点人群尿碘监测综合评价中的应用

赵向阳，孙爱峰，孙齐蕊

1.白城市疾病预防控制中心，吉林白城 137000；2.白城市卫生急救中心，吉林白城 137000；3.吉林大学公共卫生学院，吉林长春130021

碘缺乏病是我国重点防制的一种生物地球化学性疾病。疾病监测是碘缺乏病防制的一种重要措施，包括随机抽样调查居民食用碘盐监测、大型集体用餐重点单位碘盐食用情况监测、重点人群尿碘水平监测和儿童碘缺乏病病情监测，各方面又有相应评价指标。考虑到某地2007—2012年重点单位碘盐食用情况和儿童碘缺乏病病情监测之间的差异无统计学意义，因此，笔者选择居民食用碘盐监测和重点人群尿碘水平监测结果为基本资料，应用秩和比法来综合评价某地2007—2012年相应监测数据，为做好疾病预防控制工作提供客观的参考依据。现报道如下。

1 资料与方法

1.1 一般资料

以某地按照监测方案所获得的2007—2012年居民食用碘盐监测和重点人群尿碘水平监测数据为基本资料，其中X1-碘盐覆盖率（%）、X2-碘盐合格率（%）和X3-合格碘盐食用率（%）为评价居民食用碘盐的指标，X4-育龄妇女尿碘适宜构成比（%）、X5-儿童尿碘适宜构成比（%）和X6-孕妇尿碘适宜构成比（%）为评价重点人群尿碘水平的指标，所得各年度的监测值见表1[1]。监测数据来自文献，真实可靠。

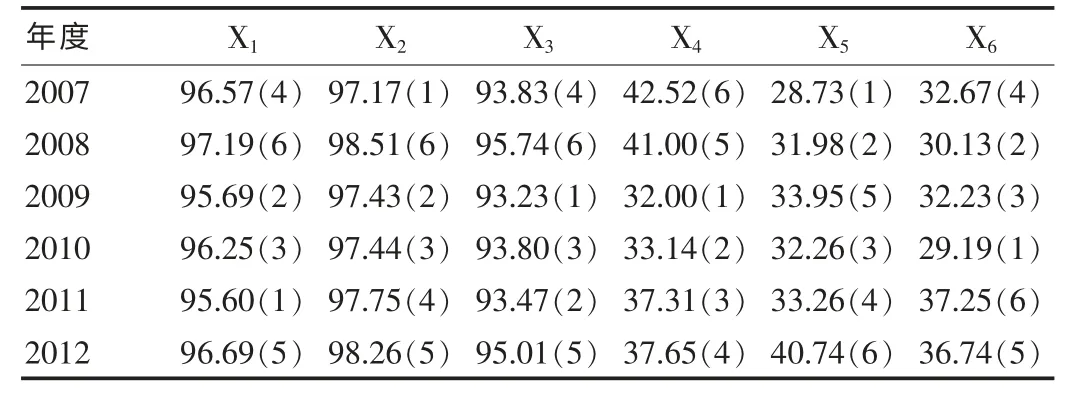
表1 某地居民食用碘盐和重点人群尿碘监测结果及其秩变换

1.2 统计方法

应用基于秩和比的可信区间法[2]分析表1 资料。首先计算由居民食用碘盐和重点人群尿碘水平监测结果所得各年度的秩和比RSR1 和RSR2，如两者Pearson 相关系数呈现正相关或无相关关系，则计算合计秩和比RSR，按可信区间法对RSR 进行综合评价；如两者之间呈负相关关系，则按可信区间法分别对RSR1 和RSR2进行综合评价。

计算各年度平方根反正弦代换值y 的95%CI 时，为减少I 类错误，按Bonferroni 法[3]校正检验水准。

2 结果

2.1 秩和比的计算

有专业知识可知，评价指标均为高优，对同一指标按从小到大顺序编秩（见表1 括号内数字），分别计算RSR1和RSR2，经计算两者相关系数为0.1832，两者之间差异无统计学意义（P＞0.05）；进而计算RSR，并按大小顺序排序，见表2。

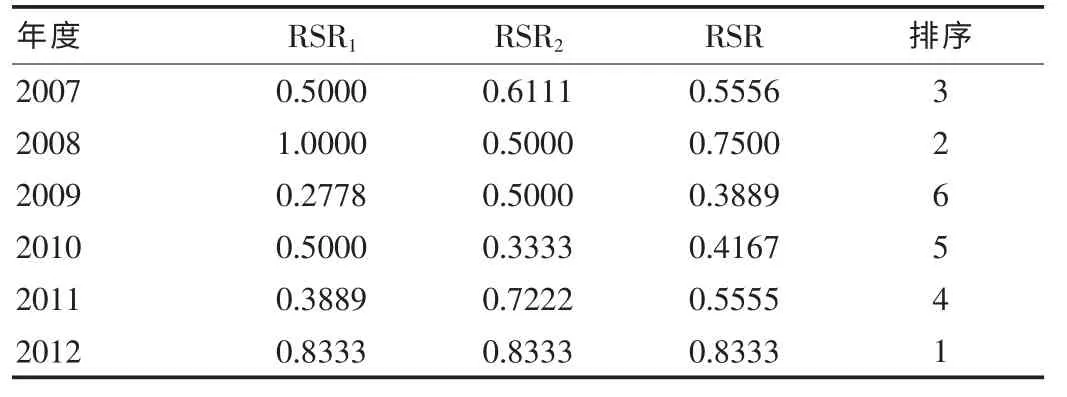
表2 各年度居民食用碘盐和重点人群尿碘监测的秩和比和排序

2.2 综合评价

计算各年度RSR 的平方根反正弦代换值y，按照公式y±3.1440 Sy 计算y 的95%CI，见表3。

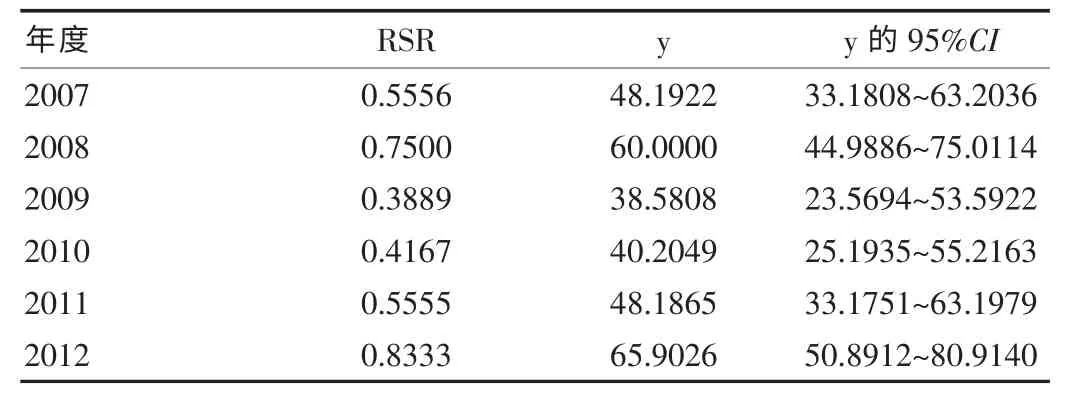
表3 各年度居民食用碘盐和重点人群尿碘监测结果的综合评价

比较各年度y 的95%CI 可知，2008年与2009年、2010年，2012年与2007年、2009年～2011年两两年度之间的差异有统计学意义（P＜0.05）；其余年度两两之间均差异无统计学意义（P＞0.05），见表4。

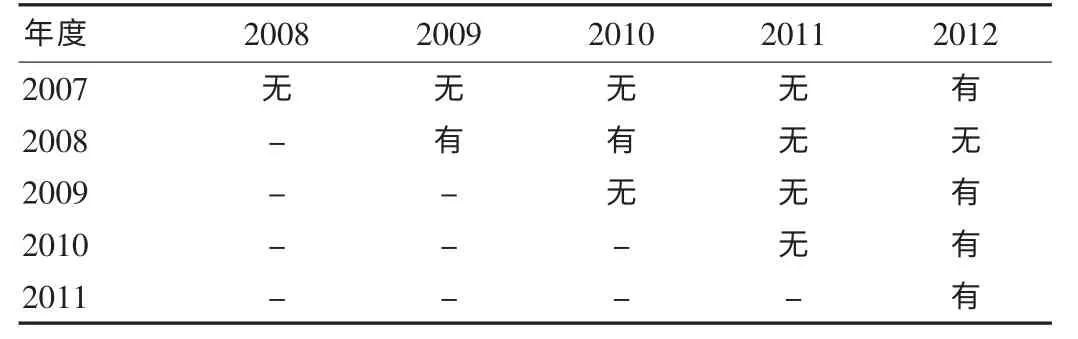
表4 两两年度之间差异是否具有统计学意义的判断

3 讨论

居民食用碘盐和重点人群尿碘监测是防制碘缺乏病的重要措施，通过监测获得的数据可以计算相应统计指标，采用适宜的统计方法在对监测数据进行综合评价，用以提高监测质量和优化监测方案，更可为碘缺乏病的防制提供可靠的参考依据，阻止疾病在人群中的发生、发展和流行。

秩和比法是由原中国预防医学科学院田凤调教授提出的一种融非参数统计和参数统计于一体的统计方法，在疾病监测数据的统计分析中得到广泛应用[4-7]。在应用秩和比法时，秩次变换应区分为高优还是低优指标，保证计算得到的秩和比越大越好；要根据研究目的的不同和被研究对象数量的多少，选择可信区间法或分档法对资料进行综合评价。

当比较组数较少时，应选择可信区间法进行两两比较。为减少I 类错误的发生，在计算RSR 变量变换值时应对检验水准进行校正，两两比较的准则是看变量变换值95%CI 交叉数值是否超过可信区间范围的一半，超过的话说明在设定的检验水准下，两者之间的差异无统计学意义，否则差异有统计学意义。当比较组数较多时，应选择分档法进行聚类分析。分档法要求按照线性分割或均数±标准差等方法至少分为2 档（等级），且各档方差齐，应用方差分析和多重比较法表明各档之间均数及其两两均数之间的差异均有统计学意义，即为最佳分档。可见基于秩和比的可信区间法和分档法的原理的不同的。

表1 资料给出的评价指标分属居民食用碘盐和重点人群尿碘监测，直接将其编秩计算秩和比是不合理的。此时应计算类秩和比RSR1 和RSR2 的Pearson 或其他相关系数，如呈正相关或无相关关系则计算合计秩和比RSR 并进行综合评价；如呈负相关关系，为避免合计秩和比所产生的相互抵消作用，则分别对RSR1 和RSR2 进行综合评价。由于该文资料所得Pearson 相关系数为0.1832，两者之间差异无统计学意义（P＞0.05），所以应进一步计算各年度的合计秩和比，以客观反映各年度居民食用碘盐和重点人群尿碘监测数据表现出的综合作用。值得注意的是，通常认为居民食用碘盐和重点人群尿碘水平之间应该是呈正相关关系的，但该文却得出无相关关系的结论，这里的原因可能是多方面的，值得进一步开展相关流行病学调查进行研究和探讨。

该资料计算得到2007年和2011年的RSR 均为4/9，这是由于秩次变换只考虑数值之间的大小关系所致。此时可采用其他秩次变换方法，由于数值保留到千分位均可做进位处理，笔者试以2001年各指标数值的增长幅度合计数值大小决定哪一年度进位哪一年度不进位，由于该年度的增长率为-13.43%，所以2007年进位，2011年不进位，这同时也满足了秩和比加和值为（n+1）/2 的基本理论，更解决了两个年度排序相同问题。

基于以上分析可知，2007—2012年某地居民食用碘盐和重点人群尿碘监测综合排序结果为2012年＞2008年＞2007年＞2011年＞2010年＞2009年，排序结论与TOPSIS 法完全相同。该方法的优势在于可以将计算得到的秩和比进行两两比较，获得比文献[1]更为丰富的信息。同时，当年度数量较多时，尚可进行发展趋势和统计预测预警分析，这更有利于根据统计分析结果来提高监测质量和优化监测方案，为碘缺乏病的防制提供可靠的参考依据，达到阻止疾病在人群中的发生、发展和流行的目的。

碘缺乏病在我国广泛流行。《食用盐碘含量》（GB26878-2011），中规定食用盐产品（碘盐）中碘含量的平均水平（以碘元素计）为20～30 mg/kg，碘含量的允许波动范围为±30%；各省、自治区、直辖市人民政府卫生行政部门在规定的范围内，根据当地人群实际碘营养水平，选择适合该地情况的食用盐碘含量平均水平。要实现“因地制宜，分类指导，科学补碘”的防治策略，必须按照国家规定加强碘缺乏病监测工作，不断提高监测质量，进行科学统计分析，为疾病防制提供强有力的数据支撑。

[1]黎新宇,李阳桦,杜丹,等.采用TOPSIS 法对北京市2007-2012年碘缺乏病检测结果综合评价[J].中国地方病防治杂志,2014,29(3):185-186,190.

[2]孙爱峰.秩和比法在不同地区人体蛔虫感染现状调查结果综合评价中的应用[J].中国医药指南,2011,9(31):226-227.

[3]方积乾.医学统计学与电脑实验[M].第4 版.上海：上海科学技术出版社,2012.

[4]张辉,孙爱峰.秩和比法在吉林省省级大骨节病病情监测结果综合评价中的应用[J].中国医药指南,2012,10(18):377-378.

[5]姜芳晶,杨维中.医学常用综合评价方法[J].疾病监测,2006,21(6):325-328.

[6]薄桂云,孙爱峰.秩和比法在某市2006～2010年居民户碘盐监测结果综合评价中的应用[J].中国医药指南,2013,11(18):773-774.

[7]王艳萍,孙爱峰,孙齐蕊.秩和比法在中国大陆居民用户碘盐监测结果综合评价中的应用[J].中国医药指南,2014,12(35):385-386.