供应链库存成本模型的研究
李群霞,马风才,张 群
(北京科技大学 东凌经济管理学院,北京 100083)
0 引言
传统供应链库存模型假设各成员之间相互独立的,结果是优化结果是次优的。为了保证利益的最大化,必须在全局范围内进行优化。Wang[1]引入了折扣机制,供应商可以针对不同的客户进行不同程度的折扣。李群霞等[2]研究了数量折扣方法,在联合决策中引入了补贴激励机制,根据客户的订货量和订货次数,给予客户不同程度的补贴。Viswanathan和Piplani[3]研究了共同补货时间,供应商确定一个共同的补货时间,要求所有客户只能在这段时间内补货。Sajadieh[4]研究提前期对供需同步库存模型的影响,假设提前期服从负指数分布。
本文在由一个生产商和一个客户组成的2级供应链上,当客户在提前期开始点下达订货要求时,生产商启动生产,直到满足客户的多次订货要求才结束生产。本文将建立供应链库存成本模型,在全局基础上进行联合决策优化,确定最佳的订货量和订货次数,保证最小的联合决策库存成本。
1 供应链库存成本模型
缺货条件下的供应链库存涉及的具体参数定义如表1所示。图1(a)反映客户库存水平的变化情况,图1(b)反映生产商库存水平的变化情况。t1时刻末为订货点,客户向生产商订Q件产品。生产商立即响应客户的订货要求,开始生产产品。在L时刻末,生产商已生产至少Q件产品以满足客户的Q件产品的需求。Q件产品会瞬时到达,客户的库存会及时补货。生产商会一直生产产品,直到生产nQ件产品来满足客户的n次订货才结束生产。

表1 变量及其含义
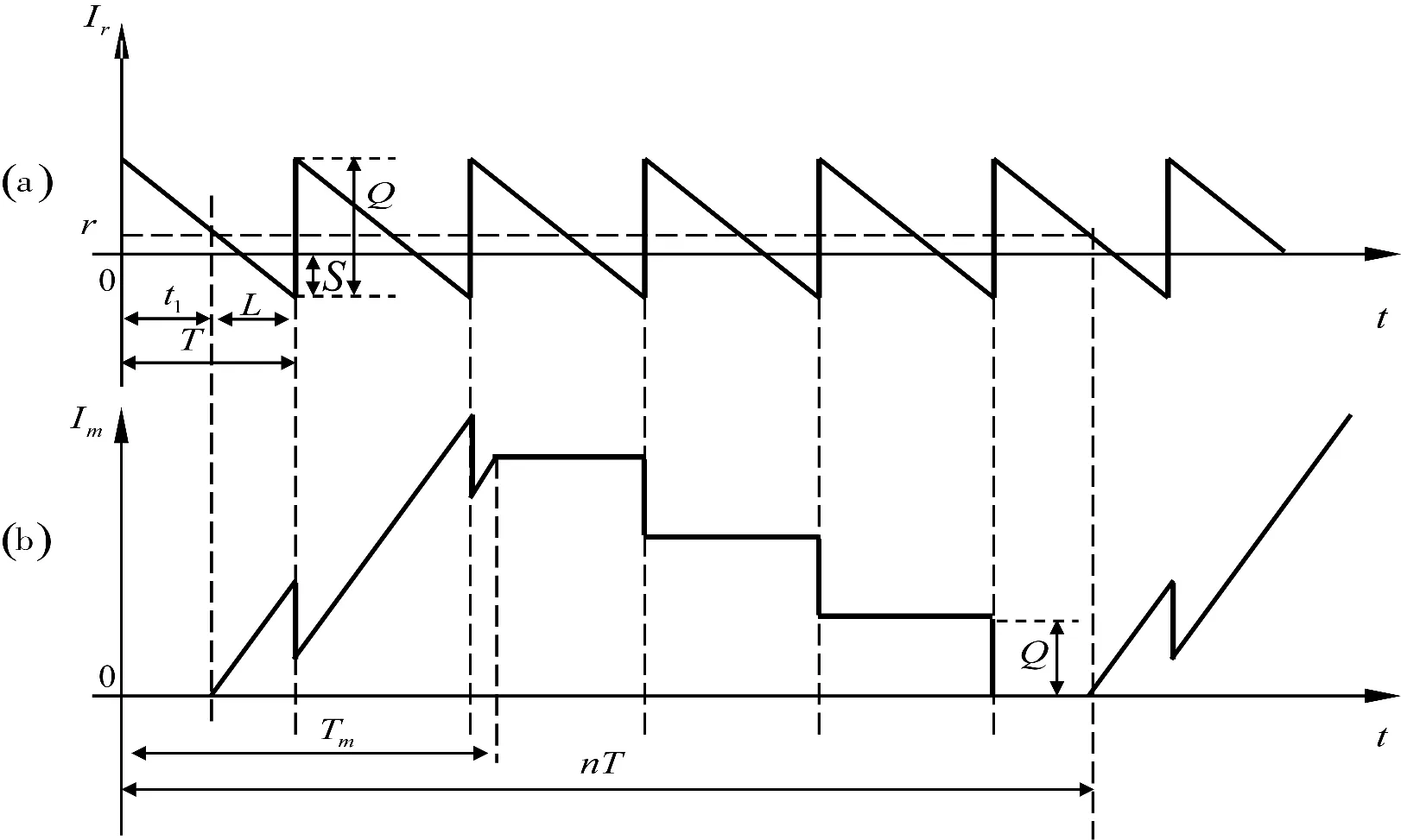
图1 客户(a)— 生产商(b)的库存变化水平
如图1(a)所示,客户平均库存成本Cr为订货成本、持有成本和缺货成本之和,即

如图1(b)所示,生产商的库存持有成本为持有成本和生产准备成本之和,即
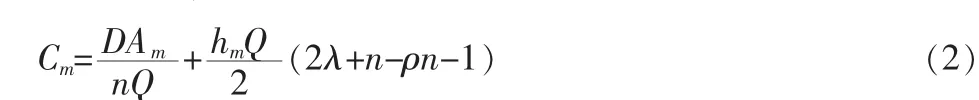
结合客户库存成本模型(1)和生产商库存成本模型(2),可得供应链联合库存成本为
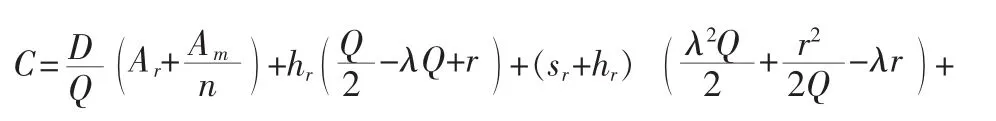

采用求导优化方法,可得最优解和最优供应链库存成本:
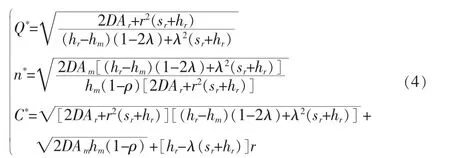
2 算例分析
假设客户和生产商的库存参数如下:
(1) 一次订货 (客户):Ar=100 元 /次,D=2000 件 /年,hr=20件 /年,sr=50 件 /年,r=50 件,λ=0.1。
(2)一次生产(生产商):Am=10000 元 /次,P=40000 件 /年,hm=10 元 /件 /年。
为了证明本文提出的优化估计方法的正确性和验证式(4)是否存在最小联合库存成本,使用穷举法搜索最佳参数估计值(n*,Q*)。 具体搜索步骤如下:
设置 n 的搜索范围[1,100],步长=1;
设置 Q 的搜索范围[1,1000],步长=1;
将不同的n值和不同的Q值代入式(4),获取不同的联合库存成本;
从上述得到的联合库存成本中,寻找最小的联合库存成本;
寻找最小的联合库存成本所对应的n值和Q值。
按照上述步骤,可搜索在n*=8,Q*=257处存在最小值C*=22380。可见穷举法搜索的结果与优化估计方法产生的结果大致相同,证明优化方法正确。如果设置更小的步长,可得到更加精确的估计值,但是这种穷举搜索法需要消耗更多的计算资源,搜索时间会更长,有时候会达到无法忍受的地步。而本文提出的优化估计方法可以快速估计出最优值,相比穷举搜索法更加优越。
3 结论
本文研究了由单一生产商和单一客户组成的2级供应链库存模型,建立了基于联合库存目标函数的供应链库存成本模型,证明了存在着最优订货量和最优订货次数。数值分析方法表明优化方法估计得到的结果与穷举搜索法搜索到的最佳结果是一致的。表明本文提出的优化方法是正确的。相比穷举搜索法,本文提出的优化方法更加有效、更有意义。
[1]Wang Q.Determination of Supplier’soptimal quantity discountschedules with heterogeneous buyers [J].Naval Research Logistics,2002,49 (1):46-59.
[2]李群霞,马风才,张群.供应链库存模型联合决策的研究[J].中国管理科学,2011,19(6):57-64.
[4]Lee CH, Rhee BD.Trade credit for supply chain coordination [J].European journalofoperational research,2011,214(1):136-146.
[3]Viswanathan S, PiplaniR.Coordinating supply chain inventories through common replenishment epochs [J].European Journal of Operational Research,2001,129(2):277-286.
[4]Sajadieh MS, Jokar MRA, Modarres M.Developing a coordinated vendor-buyer model in two-stage supply chains with stochastic leadtimes[J].Computers& operations research,2009,36(8):2484-2489.

