模糊数学与中介真值理论相结合的评价方法*
潘 茜,张育平,陈海燕
(南京航空航天大学计算机科学与技术学院,江苏 南京 210016)
模糊数学与中介真值理论相结合的评价方法*
潘 茜,张育平,陈海燕
(南京航空航天大学计算机科学与技术学院,江苏 南京 210016)
针对模糊非确定现象的评价问题,提出了模糊数学与中介真值理论相结合的评价方法。模糊数学评价法和中介真值理论的方法都是从量的角度研究和处理模糊现象。但是,模糊数学评价法注重应用而缺乏系统理论的支持,其模糊合成算子在多因素情况下很难确定,且度量值域局限于[0,1];中介真值理论的评价方法在处理因素较多且权重难以细分的情况时,也具有一定的局限性。因此,将模糊数学与中介真值相结合,将模糊数学的评价方法运用到二级指标的评定,将中介真值理论的评价方法运用到一级指标的综合评定,由此确定最佳选择方案。最后,将该方法运用于软件质量评估,并分别与模糊数学评价法和中介真值理论的评价方法相比较,结果表明该方法是可行的、合理的,并具有一定优势。
模糊数学;中介真值理论;度量值域;指标体系;质量度量
1 引言
所谓评价,即价值的确定,是通过对照某些标准来判断测量结果,并赋予一定价值。早期的评价方法有总分评定法、排队计分法、综合指数法等。这些方法简单,但原始数据遗失较大,评价结果也不够全面,因此涌现出很多评价方法,例如:层次分析法AHP(Analytic Hierarchy Process)[1]、逼近理想解排序法[2]、模糊评价法[3]、多元统计分析法[4]、灰色关联分析法[5]、遗传算法[6]、人工神经网络法[7]等,以及这些方法的改进算法。但实际生活中,很多客观事物都呈现出“亦此亦彼”的模糊现象,模糊现象是普遍而客观存在的,因此需要一种基于逻辑的、相对合理的、有效解决模糊现象的方法。
1965年美国自动控制专家查德(Zadeh L A)教授提出了模糊数学评价法,它是在模糊环境下,考虑多种因素的影响,为了某种目的对评价对象做出综合决策的方法[8]。它根据隶属度理论将定量与定性相结合,能较好地解决模糊的、难以量化的问题。模糊数学已在水质勘测、环境度量、软件度量等领域得到应用[9~11],但它完全是从应用的角度出发,缺乏系统的数学理论的支持,仍存在一些不足:(1)在因素较多,既要突出某个主要因素,又要兼顾其他因素时,模糊合成因子很难确定;(2)度量值域局限于[0,1]。
20世纪80年代,朱梧檟教授和肖奚安教授[12]提出了中介原则,中介真值理论由此诞生。中介真值理论的方法是以中介数学系统[13]为背景,通过描述数值区域与其对应谓词的关系进行数值度量的方法[14]。它的诞生,从理论上对模糊数学评价法进行了扩充。它不仅提出了介于好与坏之间的“中介”状态,而且提出了“更好”与“更坏”的超态概念。超态概念的引入,理论上使度量值域从模糊数学的[0,1]扩展为(-∞,+∞)。这将促使人们更加方便地与计算机进行对话,现已在很多领域得到运用[15~17]。但是,在因素较多的情况下,如果将其分层,那么二级指标采用中介真值理论的计算结果不仅偏小,甚至含有大量0、1和负值的情况,不利于一级指标的评定,而层次越多结果也越不准确。
因此,本文从理论与应用的双层角度出发,将模糊数学评价法和中介真值理论的评价方法相结合,根据因素集中各指标的关系进行分层,利用模糊数学评价法在单因素评价上的优势,将其运用于二级指标的评定,并将中介真值理论的评价方法运用于最终的一级指标评定。本文旨在为模糊非确定现象的处理提供一种基于逻辑的、能够被计算机理解的评价方法,为今后更深层次的研究打下基础。
2 模糊数学和中介真值理论相结合的评价方法
利用模糊数学与中介真值理论相结合的评价方法对指标体系进行评价,首先需要根据指标集中各因素的关系进行分类,用以解决因素过多、权重难以划分的问题。再将模糊数学评价方法用于二级指标的评定,中介真值理论的评价方法用于一级指标的综合评定。最终确定最佳选择方案。
2.1 中介真值理论相关定义
中介真值理论的评价法最突出的一点,就是比模糊数学评价法具有更系统的数学理论的支持,以下是中介真值理论的部分定义:
在中介数学系统中,记P为一个谓词,x为一变量,P(x)表示x完全具有性质P。符号“╕”表示 “对立于”,则╕P表示P的反对对立面。符号“~”称为模糊否定词,解释为“部分”。符号“+”表示“更”,因此+P表示比P更P。文献[14]给出了如下定义:
定义1若给定非空对象集合x,称映射F:X→Rn是对象集合X的数值化映射。
定义2对于x∈X,子集T⊂Rn和F⊂Rn分别满足:f(x)∈T↔P(x)及f(x)∈F↔╕P(x),就称T和F分别是谓词P的“真数值区域”和“假数值区域”。
定义3f是非空对象集合X的一维数值化映射,即f:X→R。与谓词P的真值对应的数值区域是闭区间[α-ε,α+ε],则称α为P的ε标准度。数值区域与谓词的对应关系如图1所示。

Figure 1 Corresponding relationship between numerical area and predicate
从图1中可以直观地看出,度量域从 [0,1]扩展为(-∞,+∞)。
定义4相对于P的距离比值函数hT:f(X)→R,当取y=f(x)∈f(X)时,
(1)
hT(y)越大,y相对于P的真值程度越大,y相对于╕P的真值程度就越小。
定义5f:X→Rn是对象集合X的n维数值化映射。当取yi=(f1(xi),f2(xi),…,fn(xi))=(yi1,yi2,…,yin)∈f(X)时,有:
对应P的距离比例和函数:
hnT-S(yi)=∑(hT(yik))
(2)
对应P的距离比例平均函数:
(3)
2.2 单因素模糊评价步骤
对单因素进行评价,主要利用模糊数学评价法,其步骤如下:
(1)对于任一对象,将其待评价的因素记为u1,u2,…,um,即评价集为U={u1,u2,…,um},如软件质量评价U={功能性,可靠性,易用性};
(2)给出评价等级集合V={v1,v2,…,vn},如V={优,中等,差};
(3)确定评价指标的权重W=(w1,w2,…,wm),且∑wi=1;
(4)通过专家打分或问卷调查等形式确定m*n的评价矩阵R,即:
(5)通过评价矩阵R和权重系数矩阵W得到模糊评判集S,即:
而∘即为模糊合成算子。
模糊合成算子有四种形式:
①M(∧,∨)算子:
Sk=∨(wj∧rjk)=max{min(wj,rjk)}
(4)
②M(·,∨)算子:
Sk=∨(wj·rjk)=max{wj,rjk}
(5)
③M(∧,⊕)算子:
Sk=min{1,∑ min(wj,rjk)}
(6)
④M(·,⊕)算子:
Sk=min{1,∑wj,rjk}
(7)
其中,M(∧,∨)算子和M(·,∨)算子比较能突出评价中起主要作用的因素,在确定W时其分量之和不一定为1;M(∧,⊕)算子和M(·,⊕)算子能够兼顾各因素的作用,W分量之和一定为1。
2.3 多因素的评定步骤
根据因素集中各指标的关系进行分类,每类有k个指标,则第二级评价因素集为Ui={ui1,ui2,…,uik},相应权重矩阵为wi=(wi1,wi2,…,wik),相应单因素评判矩阵为:
(1)根据2.2节的单因素评定步骤得到模糊评判矩阵A,即:
(8)
(2)采用中介真值理论的评价方法,记谓词P(x)表示对应程度,即对象质量为优,则╕P(x)表示对象质量差,~P(x)表示对象质量中等,+P(x)表示对象质量特优,╕+P(x)表示对象质量特差;
(3)建立P与╕P之间的标准度αF和αT,其中αF为每列最小值,αT为每列最大值,εF=εT为每列的最小距离值,并计算出αF-εF,αF+εF,αT-εT,αT+εT;
(4)根据定义4中的公式,计算出距离比例函数h(aij),得到另一个m*n阶矩阵B,即:
(5)根据定义5中的公式,分别计算出距离比例和函数和距离比例平均函数hnT-S(yi)和hnT-M(yi),并比较大小,确定最佳选择方案。
3 实验证明及分析
将模糊数学和中介真值理论相结合的评价方法用于软件质量评价中,并分别与模糊数学评价法和中介真值理论的评价方法相比较,以证明该方法的可行性和有效性。本文所用实验数据皆来自文献[18]。
本文以文献[18]中的递阶层次分析结构模型为例,包含6个一级指标和24个二级指标,如图2所示。

Figure 2 Hierarchic analysis structure model of the software quality metric
采用文献[12]中给出的权重值,其主要采用了专家排序法,所得过程我们不做过多赘述,引用目的在于验证本文所提方法的可行性。
一级指标权重为:
W=(w1,w2,w3,w4,w5,w6)=(0.27,0.22,0.15,0.13,0.17,0.06)
二级指标权重为:
w1=(0.27,0.35,0.16,0.22);w2=(0.40,0.27,0.19,0.14);w3=(0.28,0.31,0.23,0.18);w4=(0.31,0.33,0.12,0.24);w5=(0.22,0.26,0.43,0.09);w6=(0.29,0.45,0.07,0.19)
实验数据:引用文献[12]中实例分析中的数据可知,现有甲、乙、丙、丁四种软件质量的解决方案,需对这四种方案进行综合度量,并为企业推荐一种最优的解决方案。该企业聘请了领域专家对各项二级指标进行打分,并对结果进行规范化处理,所得结果如表1所示。
(1)采用2.2节中单因素模糊评价步骤分别对二级指标进行评定:由于需要兼顾每个因素的作用,所以选择M(·,⊕)算子,根据式(7)和式(8)计算得一级指标评价结果,如表2所示。
(2)利用2.3节中中介真值理论的评价方法对表2中的结果进行计算,根据定义5中式(1)~式(3),分别计算得到距离比例函数h(aij)、距离比例和函数hnT-S(yi)、距离比例平均函数hnT-M(yi),如表3所示。从距离比例和函数和距离比例平均函数值可以看出,就优越性而言,丙方案优于其他三种方案,乙方案为备选方案。
(3)用模糊数学评价法和中介真值理论的评价方法分别对其进行计算,并比较结果。
①采用模糊数学评价法,对二级指标评价结果不变,但是模糊合成算子的选择会对结果产生很大影响,分别采用四个算子,根据式(4)~式(7)对一

Table 1 Software quality evaluation results of the second level index表1 软件质量二级指标评价结果

Table 2 Software quality evaluation results of the first level index表2 软件质量一级指标评价结果

Table 3 Distance ratio function value,sum distance ratio function value and average distance ratio function value表3 距离比例函数值、距离比例和函数值和距离比例平均函数值
级指标进行评价,所得结果如表4所示。
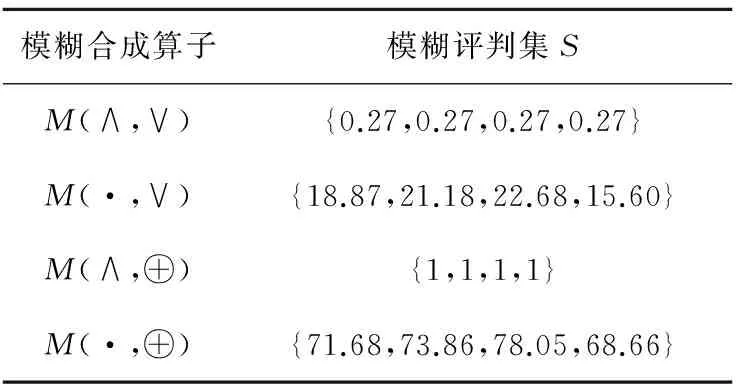
Table 4 Evaluation results of the four fuzzy synthesis operators表4 四个模糊合成算子评价结果
由表4可以看出,M(∧,∨)和M(∧,⊕)所得结果根本无法起到评价作用,那是因为权重值的大小和各指标的分值大小之间存在很大差距;M(·,∨)和M(·,⊕)中,如果只根据最大隶属度原则进行选择,只考虑了隶属度最大的点,其他点都没有考虑,信息损失大。由此可见,模糊数学评价法在模糊合成算子和评价原则选择上都存在一定问题,一旦选择不当,就会对评价结果产生重大影响。
②采用中介真值理论的评价方法,对二级指标评价过程过于繁琐,所得结果也非常小,含有很多0、1值,甚至在一些情况下会含有负值,如功能性U1的二级指标评价结果:
Bi中含有大量的0和1,对其进行一级指标评定所得结果具有很大争议性,尤其是结果中出现负值的时候,评价结果无法使人信服。一旦我们采用三级、四级的分层方式时,这样的现象将更为明显,例如我们将上式B1采用中介真值理论的评价方法进行若干次计算,结果如下:
B12=…=B1n
从以上结果可以看出,以后的计算结果与第一次所得结果完全相同,失去了分层的意义。
从以上三者的比较中可以看出,模糊数学和中介真值理论相结合的评价方法是最为合理有效的,既排除了模糊数学评价方法中模糊合成算子的影响,又使得在使用中介真值理论的评价方法时,不受0、1及负数的制约,所以最终评定丙方案为最佳方案,乙方案为备选方案。
4 结束语
本文通过对以往各种评价方法的学习和比较,从理论和实际应用相结合的角度出发,设计出了一种新的、基于逻辑的评价方法。该方法将模糊数学评价法与中介真值理论的评价方法相结合,利用模糊数学在处理单因素问题上的优势,将其用于二级指标的评定;利用中介真值理论评价法在度量域上的优势,以及其强有力的数学理论支持,将其运用于一级指标的综合评定。最后将该方法用于软件质量评价中,以综合考虑多方因素为实质,分别与模糊数学评价法和中介真值理论的评价方法相比较,计算结果准确,计算过程简单,便于计算机理解,更利于实际项目中指标的评价。
[1] Liu Chih-ming,Hsu Hen-shen,Wang Shen-tsu,et al.A performance evaluation model based on AHP and DEA[J].Journal of the Chinese Institute of Industrial Engineers,2005,22(3):243-251.
[2] Zhang Yi,Qiu Hai-li,Zhu Jiang. Improved TOPSIS on supplier evaluation and preference[J]. Journal of Henan University of Science and Technology(Natural Science),2013,34(3):100-104.(in Chinese)
[3] Sunday D M.A very fast substring search algorithm[J].Communications of the ACM,1990,33(3):132-142.
[4] Sheikh H R,Sabir M F,Bovik A C.A statistical evaluation of recent full reference image quality assessment algorithms[J].IEEE Transactions on Image Processing,2006,15( 11):3440-3451.
[5] Charras C,Lecroq T. Handbook of exact string-matching algorithms[M]. London:King’s Colledge London Publications,2004.
[6] Jin Ju-liang,Cheng Jian,Zhang You-fu.The fuzzy comprehensive evaluation model based on acceleration parallel genetic algorithm[J].Water Resources and Power,2005,23(6):1-4.(in Chinese)
[7] Guo Chen,Parsa V. Nonintrusive speech quality evaluation using an adaptive neuro fuzzy inference system[J].IEEE Signal Processing Letters,2005,12(5):403-406.
[8] Li Xi-can,Wang Jing,Shao Xiao-mei.Progress in the application of fuzzy mathematical method in the evaluation of land resources in Chinese[J].Progress in Geography,2009,28(3):409-416.(in Chinese)
[9] Wei Lin,Huang Feng,Li Lin.Discussion and application of the modified multilevel fuzzy comprehensive evaluation method for surface water[J]. Environmental Protection Science,2013,39(4):136-141.(in Chinese)
[10] Ding Kuang-ping,Chen Bing-hong.Application of fuzzy mathematics in environment quality evaluation[J].Journal of Zhejiang Education Institute,2002,3(3):58-62.(in Chinese)
[11] Zhu Hua-qing,Ye Jun-yao,Zou Zheng.Research on estimation of measurement of software test in fuzzy math[J]. Computer and Modernization,2007,5(3):17-19. (in Chinese)
[12] Zhang De-zhi.Application research on function of medium truth scale [D].Nanjing:Nanjing University of Technology,2008.(in Chinese)
[13] Xiao Xi-an,Zhu Wu-jia.Propositional calculus system of medium logic(I) [J].Journal Nature,1985,4(8):315-316.(in Chinese)
[14] Hong Long,Xiao Xi-an,Zhu Wu-jia.Measure of medium truth scale and its application (I) [J].Chinese Journal of Computer,2006,29(12):2186-2193.(in Chinese)
[15] Rong Zhou.Weighted data fusion in wireless sensor networks based on medium theory [J]. Journal of Electronic Measurement and Instrument,2010,24(8):705-712.(in Chinese)
[16] Du Bo,Shen Ling,Wang Liang. Fuzzy comprehensive evaluation of construction quality based on analytic hierarchy process and measure of medium truth scale [J]. Mathematics in Practice and Theory,2011,41(15):66-74. (in Chinese)
[17] Li Ai-qun, Zhang Lian-jie. Grade evaluation algorithm scheme based on medium truth scale [J]. Computer Tech-
nology and Development,2010,20(7):164-167.(in Chinese)
[18] Du Jin-huan,Jin Lu-lu. Research on process and model of software quality metrics [J].Computer Technology and Development,2014,24(4):38-40.(in Chinese)
附中文参考文献:
[2] 张毅,丘海礼,朱江.改进逼近理想解排序法的供应商评价和优选[J].河南科技大学学报(自然科学版),2013,34(3):100-104.
[6] 金菊良,程健,张有福.基于加速并行遗传算法的模糊综合评价模型[J].水电能源学,2005,23(6):1-4.
[8] 李希灿,王静,邵晓梅.模糊数学方法在中国土地资源评价中的应用进展[J].地理科学进展,2009,28(3):409-416.
[9] 魏琳,黄丰,李琳.地表水多级模糊数学评价法修正应用探讨[J].环境保护科学,2013,39(4):136-141.
[10] 丁匡平,陈兵红.模糊数学在环境质量评价中的应用[J].浙江教育学院学报,2002,3(3):58-62.
[11] 朱华清,叶君耀,邹正.软件测试度量的模糊数学评价方法研究[J].计算机与现代化,2007,5(3):17-19.
[12] 张德志.中介真值度量函数应用研究[D].南京:南京工业大学,2008.
[13] 肖奚安,朱梧槚.中介逻辑的命题演算系统(Ⅰ)[J].自然杂志,1985,4(8):315-316.
[14] 洪龙,肖溪安,朱梧槚.中介真值程度的度量及其应用(Ⅰ)[J].计算机学报,2006,29(12):2186-2193.
[15] 戎舟.基于中介理论的无线传感器网络加权数据融合[J].电子测量与仪器学报,2010,24(8):705-712.
[16] 杜博,申玲,王亮.基于层次分析和中介真值度量的工程质量模糊综合评判[J].数学的实践与认识,2011,41(15):66-74.
[17] 李爱群,张廉洁.基于中介真值程度的成绩评价算法[J].计算机技术与发展,2010,20(7):164-167.
[18] 杜金环,金璐璐.软件质量度量过程及模型研究[J].计算机技术与发展,2014,24(4):38-40.

潘茜(1990-),女,江苏南京人,硕士生,研究方向为软件工程。E-mail:420617478@qq.com
PAN Qian,born in 1990,MS candidate,her research interest includes software engineering.
A new valuation method based on fuzzy mathematics and medium truth theory
PAN Qian,ZHANG Yu-ping,CHEN Hai-yan
(School of Computer Science and Technology,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)
Aiming at the evaluation of fuzzy and non-deterministic phenomenon, we propose an evaluation method based on fuzzy mathematics and the medium truth theory. Both the fuzzy mathematics method and the medium truth theory method study and deal with the fuzzy phenomenon from the angle of quantity. But fuzzy synthetic operator of the fuzzy mathematics method is difficult to determine when there are multiple factors, and the measurement range limit in [0,1]. The medium truth theory method also has some limitations in dealing with the situation of multiple factors when evaluate the secondary indicators. Therefore, we combine the fuzzy mathematics method and the medium truth theory method: using the former to evaluate the secondary indicators, and the latter for the first indicators, thus the best option is obtained. Finally, we apply the proposed method to software quality evaluation and compare its results with those of the fuzzy mathematics method and the medium truth theory method, Test results show that our method is feasible and reasonable, and has certain advantages.
fuzzy mathematics;medium truth theory;measurement range;indicator system;quality measures
1007-130X(2015)09-1676-06
2014-09-16;
2015-01-16基金项目:国家973计划资助项目(2014CB744900);南京航空航天大学研究生创新基地开放基金资助项目(kfjj201460)
TP311.5
A
10.3969/j.issn.1007-130X.2015.09.013
通信地址:210016 江苏省南京市秦淮区御道街29号南京航空航天大学计算机科学与技术学院
Address:School of Computer Science and Technology,Nanjing University of Aeronautics & Astronautics,29 Yudao St,Qinhuai District,Nanjing 210016,Jiangsu,P.R.China

