双层高架桥门式墩与独柱墩抗震性能比较分析

鲁传安

（上海市政工程设计研究总院（集团）有限公司，上海市200092）

1 概述

近年来我国经济得到了迅猛发展，城市土地资源的稀缺及桥梁建设用地的紧张日显突出。为了在有限的土地资源上极大地提高城市交通的使用效率、改善桥梁通行条件，双层高架桥便应运而生，其中以上层市政高架道路下层轨道交通的双层高架应用越来越广泛[1]。双层高架桥结构比较复杂，震害与一般高架有所不同。在1989年洛马普里埃塔（Loma Prieta）地震中，美国旧金山海湾地区的双层高架桥大多出现了损伤，其中赛普拉斯（Cypress）双层高架桥的倒塌造成了较大的人员伤亡和财产损失。从而引起了广大学者对双层高架桥抗震性能研究的重视，也取得了一定的研究成果[2]、[3]。

本文基于国内某工程实例，针对上层公路下层轨道交通的双层高架桥进行分析。该工程采用桥面连续结构简支箱梁结构，其中以混凝土箱梁为主，辅以跨路口的大跨径钢砼叠合箱梁。上层桥宽18 m，下层轨道交通单线宽4.3 m，双线宽8 m，标准跨径为30 m、35 m及40 m三种。下部结构采用门式墩和独柱墩两种形式，基础为钻孔灌注桩。典型独柱墩及门式墩立面布置图如图1、图2所示。本文桥墩采用延性抗震设计方法，即墩柱按延性构件设计，横梁、塑性铰区抗剪及桩基础按能力保护构件设计。

图1 门式墩立面布置图

2 动力计算模型及动力特性

2.1 动力计算模型

图2 独柱墩立面布置图

为了研究比较两种桥墩的抗震性能，分别选取两联标准跨径为40 m且为标准宽度的桥梁结构进行抗震分析，同时为了考虑相邻结构的影响，建模时将相邻桥跨也一并模拟，两个模型选取的墩柱总高度也基本一致，在25 m～29 m之间。

主梁和桥墩均采用空间梁单元模拟。在支座模拟时，将弹性支座处理为主梁和墩顶采用弹簧单元模拟，由于主梁和墩顶之间每排均设有多个支座，在模型中均进行了适当的合并。在地震反应分析中，考虑到桩基础的刚度和土层的特性对结构地震响应的影响，桥梁桩基础通过在承台底部加上六个方向的弹簧来模拟桩基础的作用。为了能更真实模拟实际情况，建模过程中考虑了上层桥面连续部分的影响，而下层是轨道交通,建模时把轨道对主粱的连接作用也考虑进去。门式墩及独柱墩动力计算模型分别如图3、图4所示。

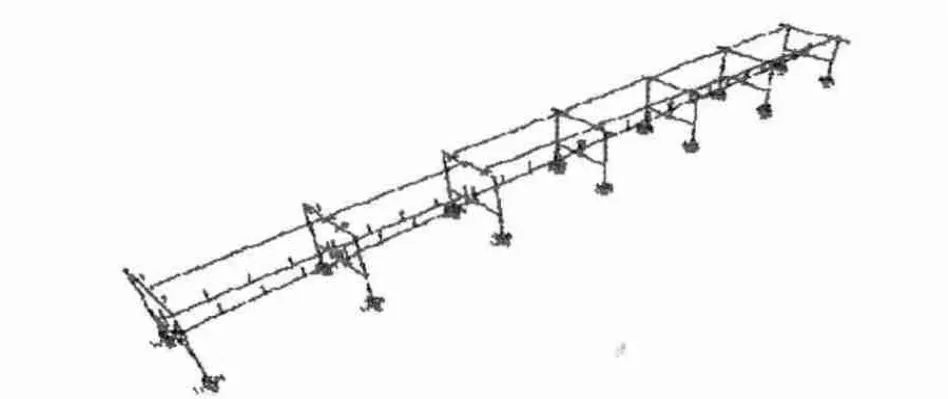
图3 门式墩动力计算模型

图4 独柱墩动力计算模型

2.2 动力特性

分析和认识桥梁的动力特性是进行结构抗震性能分析研究的基础，根据图3、图4的动力计算模型，对两种桥墩结构模型进行动力特性分析，结果如表1所列。

由表1可知，两个模型的第一阶振型均为纵飘，表明纵向刚度均较横向刚度小。而门式墩模型第一阶振型周期短于独柱墩，说明门式墩纵向刚度大于独柱墩。其次，门式墩模型第一阶横向振型出现在第7阶，独柱墩模型第一阶横向振型出现在第3阶，可见门式墩横向刚度更大。

3 反应谱分析

在前述动力特性分析所采用的结构有限元模型中，分别输入50 a10%超越概率（相当于E1地震）及50 a3%超越概率（相当于E2地震）、阻尼比为5%的场地加速度反应谱，反应谱见图5所示。输入方向组合分别为：纵向＋竖向和横向+竖向。计算结果取前300阶进行组合，组合方式为CQC组合，计算结果汇于表2～表5。

表1 结构的动力特性表

图5 地震影响系数反应谱图示

由表2～表5可知，横梁地震反应门式墩均大于独柱墩，特别是横向地震反应门式墩远大于独柱墩，门式墩剪力效应一般都大于独柱墩，而弯矩效应则是除上层柱顶位置外，其余均是门式墩纵向大，独柱墩横向大。可见，大部分的地震反应均是门式墩较独柱墩大。两者上部结构质量一致，而且墩柱高度也接近。造成这一现象的主要原因是两者动力特性差异。由前述动力特性可知，门式墩周期要低于独柱墩，对应的反应谱值则是门式墩大，从而地震反应也相应较大。独柱墩下柱和上柱底弯矩较大的原因，则是独柱墩为静定体系，横向受力主要由立柱承担，门式墩则由于本身的框架体系，横向受力由立柱和横梁共同承担。

表2 墩柱E1地震反应一览表（50 a10%）

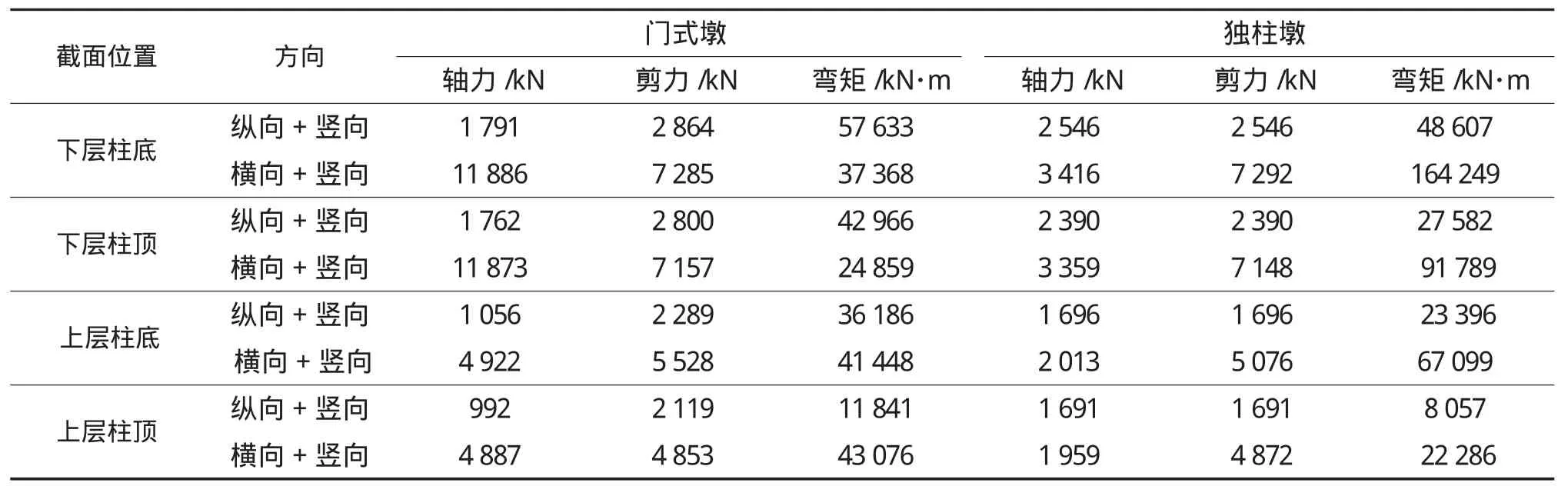
表3 墩柱E2地震反应一览表（50 a3%）

表4 横梁E1地震反应一览表（50 a10%）

表5 横梁E2地震反应一览表（50 a3%）

根据抗震规范对关键截面强度进行验算,结果表明，在E1地震作用下，独柱墩墩身、桩基础满足强度抗震要求。在E2地震作用下，横桥向独柱墩墩底发生屈服。桥墩上、下横梁满足强度抗震要求；门式墩下层柱底、上层柱顶底截面在水准EI地震作用下，横向抗弯能力已不能满足需求，在E2地震作用下，除上层柱顶截面纵向未屈服以外，其余均进入屈服状态。桩基础在E1地震作用下强度满足要求。门式墩的上下横梁强度满足抗震要求。

4 非线性时程分析

根据反应谱的分析结果，可以知道在E2地震下大部分墩柱发生损伤。因此，为了确保在该水准地震作用下，各构件满足预期的抗震性能要求，尤其是墩柱进入损伤后的延性变形情况，需采用非线性时程分析方法进行分析。

在时程计算中，墩、柱的非线性特性通过采用集中塑性铰梁单元模拟。在每个墩的屈服位置设置一个塑性铰。塑性铰的参数根据墩、柱的截面的实际配筋情况计算的弯矩-曲率关系来确定。

时程分析的地震输入组合为纵向＋竖向和横向＋竖向，竖向加速度取为横向或者纵向的0.5，考虑到地震动的随机性，对符合概率水准的六条地震波进行了计算，取其平均值作为时程计算的结果。同时，对塑性铰变形、塑性铰区域抗剪及桩基进行验算，表6、表7有代表性地列出了E2地震下墩底截面塑性铰地震响应及验算结果。门式墩其余位置塑性铰验算及桩基验算结果限于篇幅未列出。

表6 E2地震墩底截面塑性铰转角能力验算结果表（单位：rad）

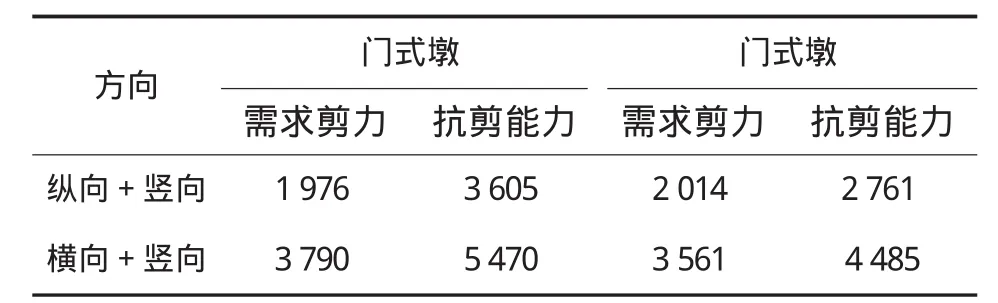
表7 E2地震墩底截面塑性铰位置抗剪能力验算结果表（单位：kN)

通过表6、表7所列的验算结果可知，在反应谱分析发生屈服的桥墩墩柱，发生的最大塑性转角小于容许的塑性转角，表明变形是满足要求的。塑性铰位置的墩身抗剪能力都满足抗震要求。门式墩与独柱墩墩底塑性铰转角变形及剪力基本接近，说明屈服后两者墩底性能基本一致。根据桩基础验算结果，在E2地震下横桥向，两种桥墩桩基均发生屈服，不能满足能力保护构件设计要求，需要加强桩基础设计。

5 结论

通过以上分析，可以得到以下主要结论：

（1）两种桥墩的动力计算模型第一阶振型均是主梁的纵飘振型，但是门式墩模型周期较独柱墩短，且门式墩横向振型出现阶数较高。

（2）门式墩和独柱墩上下横梁均未发生损伤进入屈服状态，说明横梁设计符合能力保护构件设计要求。

（3）反应谱分析地震反应，总体上门式墩比独柱墩大。独柱墩立柱在E1地震作用下仍处于弹性状态，在E2地震下仅墩底发生屈服；门式墩立柱部分关键截面在E1地震下已发生损伤，在E2地震下，除上层柱顶纵向未屈服以外，其余均发生屈服。

（4）非线性时程分析表明，两种桥墩的塑性铰转角变形及抗剪性能比较接近，且均能满足抗震要求。

[1]孙建渊，陈阶亮.城市桥梁双层交通的概念设计[J].桥梁建设，2006，（2）:39-42.

[2]张洁，李建中，管仲国.双层高架桥拟静力实验研究[J].结构工程师，2012，28（6）:128-133.

[3]彭天波，李建中，范立础.能力设计方法在双层高架桥梁抗震设计中的应用[J].世界桥梁，2009，（1）:12-15.