《数学汇编》中的3个问题在大学物理中的体现*
吴 英
(遵义师范学院物理与机电工程学院,贵州 遵义 563002)
帕普斯作为一位对古希腊数学有着全面研究的学者,他的著作《数学汇编》对于研究西方乃至世界数学的继承、发展以及相互间的影响都有着重要的价值.《数学汇编》第8卷,主要是讨论理论力学,包括与重心相关的问题,重物在斜面上的平衡以及机械力,机械器具的原理、制作及使用等问题[1].而本文主要论述《数学汇编》中的3个问题在大学物理中的体现.
1 质心的确定与帕普斯命题


图1
2 热力学奥拓循环的效率与帕普斯中项问题
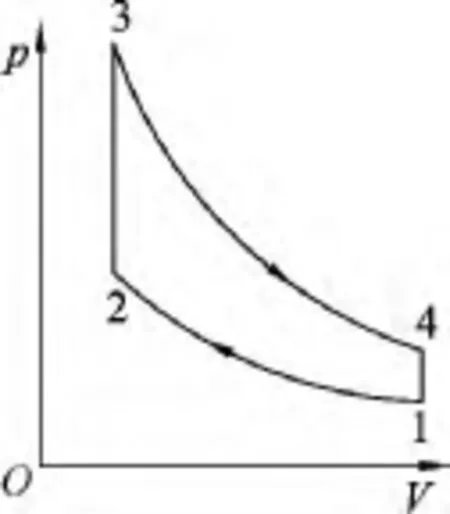
图2

3 开普勒行星天球与帕普斯5种正立方体内切、外接天球
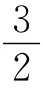

图3
开普勒是一个深受毕达哥拉斯和柏拉图影响的数学家,他用古希腊人早已发现的5个正多面体,即“柏拉图立体”,也是《数学汇编》中提到的正四面体、正六面体、正八面体、正十二面体和正二十面体,和当时已知的6颗行星的轨道套叠来解释6颗行星为什么按照那样大小的轨道运行.[10]他在《宇宙的奥秘》中提出,已知的6颗行星水星、金星、地球、火星、木星和土星,其离太阳的相对距离正好可以用5种正多面体加以分隔开来.如图3,开普勒最初设计的方案为:土星轨道,正立方体,木星轨道,正四面体;火星轨道,正十二面体;地球轨道,正二十面体;金星轨道,正八面体,水星轨道.[11]然而,在尝试了19中想象的路径并由于或多或少的观测值不一致而又否定它们之后,开普勒才发现真实的轨道,即一种椭圆轨道,进而总结出开普勒“椭圆路径定律”(开普勒第一定律)和“面积定律”(开普勒第二定律)、周期与平均半径关系的“和谐定律”(开普勒第三定律).[12]当然,在开普勒的心目中,5种层层嵌套的正多面体的宇宙模型,比声名远播的开普勒三定律更让他喜爱.
均匀薄板的质心、奥拓循环的效率和宇宙行星轨道等问题是大学物理学中的问题,与帕普斯《数学汇编》中帕普斯命题、中项问题和正立方体内切、外接天球等问题息息相关,这里让我们再次体会到数学与物理学的紧密联系.
1 邓可卉,杨坤.《数学汇编》中的数学问题在中国——兼与古希腊数学思想比较[J].自然辩证法通讯,2012,34(2):29-35,125-126.
2 杨坤.帕普斯的《数学汇编》及其问题在中国[D].内蒙古:内蒙古师范大学硕士学位论文,2009.
3 郜舒竹,刘莹.用“帕普斯——古尔丁定理”解释“喇叭悖论”[J].数学的实践与认识,2007,37(8):175-179.
4 李艳丽,王逸迅.旋转体体积的计算方法[J].西安理工大学学报,2008,24(3):362-365.
5 杨朝明.均匀平面薄片重心公式的推导[J].武警学院学报,2002,18(2):87-88.
6 费恩曼,莱顿,桑兹.费恩曼物理学讲义[M].上海:上海科学技术出版社,2005:195-198.
7 刘克哲,张承琚.物理学(第4版)[M].北京:高等教育出版社,2012.
8 王明美 .平面组合图形质心的计算[J].合肥师范学院学报,2011,29(3):35-36.
9 肖学雷.一类异型匀质平板质心的简明计算方法[J].大学物理,2006,25(12):26-28.
10 李艳平,申先甲.物理学史教程[M].北京:科学出版社,2003:89-91.
11 I·伯纳德.科恩,张卜天译.新物理学的诞生[M].长沙:湖南科学技术出版社,2010:107-124.
12 桂起权,沈健.物理学中的哲学[M].武汉:武汉大学出版社,2012:34-38.
13 张三慧.大学物理学(第3版)[M].北京:清华大学出版社,2011:94-97.

