桥梁车桥耦合振动的简化算法

蔡忠华 ，杨 军

(1.武汉市政工程设计研究院有限责任公司，湖北武汉430023；2.武汉市公路勘察设计院，湖北武汉 430015)

0 引言

随着我国经济的发展，车辆荷载及运行速度都大大的提高，桥梁结构的车桥耦合问题也越来越突出。在对桥梁结构的振动分析中，移动车辆荷载的模型主要有：常量力模型、集中质量模型、弹簧-质量模型、单轴及双轴车辆模型等。本文在既有的研究基础上，将移动车辆荷载简化成时变三角形荷载用于车桥耦合分析，并建立有限元分析模型，通过算例与既有文献资料的对比，验证了该方法的可行性，分析方法可为同类振动研究提供参考。

1 单轴车桥耦合振动数值模型

在工程实践中，如果移动荷载的质量比梁的质量小很多，此时可以不考虑移动车辆的阻尼力及惯性力，就相当于仅考虑移动荷载的重力作用，将其用一个移动的力P（t）来表示。

假设梁为等截面（EI为常数），恒载质量均匀分布（单位长度梁的质量m为常数），阻尼为粘滞阻尼（即阻尼力与结构的振动速度成正比），阻尼效应和质量及刚度性质成正比，荷载以匀速v在梁上通过，梁的运动满足小变形理论并在弹性范围内，按照图1所示的坐标系，梁的振动微分方程可用式（1）表示：

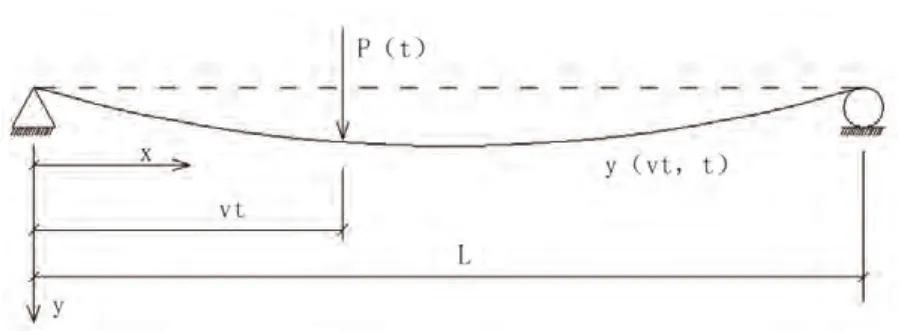
图1 移动力P(t)作用下的模型

式中：c为阻尼系数；δ为Dirac函数。

Dirac函数的特性：

式（1）是一个偏微分方程，可按振型分解法求解。振型分解法的基本原理是将结构的几何坐标变换成振型幅值坐标或广义坐标。对一维的连续体，这一边换的表达式为：

式中：qi（t）为广义振型坐标，是时间t的函数；φi（x）为主振型函数。

由式（5）可以看出，结构的任一合理位移都可以由此结构具有相应振幅的各个振型的叠加表示，即可以得到系统的完整响应。

2 车桥耦合振动的程序简化实现

在ANSYS程序中实现车桥耦合的简化计算步骤如下：

（1）建立桥梁的空间有限元模型，并进行模态分析输出桥梁模态信息；

（2）将车辆荷载简化成随时间变化的三角形荷载 P（t）（见图2）存储到数组中；

图2 将车辆荷载近似为三角形荷载图

（3）在ANSYS中使用循组模拟车辆移动，进行车桥耦合分析。

在图2中，t1=t2/2划分单元长度/车速。为了验证该方法的正确性，现分析车辆通过简支梁桥模型时桥梁的动力响应，并将计算结果与文献[1]的结果比较。简支梁桥模型跨度L=25 m,截面惯性矩I=2.9 m4,弹性模量E=2.87 GPa,线密度m=2 303 kg/m,车辆模型的质量ms=5 750 kg,移动速度v=27.78 m/s。桥梁有限元模型有100个空间梁单元组成，不考虑阻尼及路面不平顺影响。桥梁跨中挠度和竖向加速度时程曲线见图3，文献[1]的结果如图4所示，桥梁跨中位移响应本文方法最大值为2.415 mm，文献中为2.405 mm；桥梁跨中竖向加速度响应本文方法最大值为0.3380 m/s2，文献中为0.3425 m/s2，误差分别为0.42%和1.31%。对比可见本文计算结果与文献[1]结果吻合良好，说明本方法的正确有效。

图3 本文计算模型结果

图4 文献[1]计算结果

3 结论

本文提出将移动车辆荷载转化成三角形时变荷载，通过与ANSYS软件平台结合，实现车桥耦合振动的简化计算。算例分析结果与相关文献吻合，证明了该方法的可行性。该方法简化了车桥振动的分析过程，可为各种类型的桥梁车桥振动分析提供参考。

[1]C.J.Bowe,T.P.Mullarkey.Wheel-Rail Contact Elements Incorporating Irregularities[J].Addvances in Engineering Soft，2005（36）:827-837.