自由曲面混凝土结构力学特性

崔国勇，崔昌禹，2，涂桂刚

（1.哈尔滨工业大学土木工程学院，黑龙江哈尔滨150090；2.哈尔滨工业大学结构工程灾变与控制教育部重点实验室，黑龙江哈尔滨150090）

自由曲面混凝土结构力学特性

崔国勇1，崔昌禹1，2，涂桂刚1

（1.哈尔滨工业大学土木工程学院，黑龙江哈尔滨150090；2.哈尔滨工业大学结构工程灾变与控制教育部重点实验室，黑龙江哈尔滨150090）

为了研究自由曲面混凝土结构的力学性能，合理选取混凝土材料本构方程，利用有限元分析软件ABAQUS，建立自由曲面混凝土结构的有限元分析模型，通过与相关试验的对比验证有限元模型的正确性.研究典型自由曲面结构的内力分布特性、荷载-位移曲线与破坏模式、初始缺陷.结果表明：薄膜第一主应力在负高斯曲率区受拉较大，正高斯曲率区受拉较小；薄膜第二主应力在正高斯曲率区受压较大，负高斯曲率区受压较小；上、下表面第一主应力分布模式类似；结构在正、负高斯曲率过渡区的弯曲内力与薄膜内力比值较大，其他位置很小；荷载-位移曲线没有下降段，结构破坏模式为强度破坏；结构对初始缺陷的影响很小.对2个实际工程进行力学分析，验证了所归纳力学特性的正确性.

壳体结构；形状优化；ABAQUS；自由曲面

自由曲面与初等解析曲面（球面型、椭圆面型、圆柱面型、双曲抛物面型等）不同，它任意性强、形式多样，具有良好的建筑艺术效果.越来越多的建筑师关注自由曲面的灵活性，试图利用自由曲面来表现建筑思想，实现建筑意图.目前，自由曲面结构已成为新的空间结构形式，研究这种曲面结构具有何种普遍的力学性能、具有何种共同的特性，是十分必要的.

初等解析曲面结构是常用的空间结构形式之一，目前通过长期的实践与系统的研究已基本总结了该类结构的力学性能与特性.祝恩淳等[1]编写了混凝土薄壳的非线性程序，通过试验研究圆柱壳的稳定问题，指出初始几何缺陷对薄壳结构的临界荷载及屈曲性质有显著的影响.唐如意等[2-3]对钢-混凝土组合肋壳进行非线性研究，指出初始缺陷在跨度的1/300范围内，临界荷载下降值为27％～36％.何广乾等[4]推导了考虑非线性弹性稳定的椭圆抛物面壳临界荷载，指出局部稳定的临界荷载远低于总体失稳时的上临荷载，设计中局部失稳是需要考虑的控制因素，壳体缺陷将大大降低壳体的稳定性，缺陷模型的承载力为无缺陷模型承载力的51％～60％，可见常规壳体对缺陷的影响较敏感.

与传统曲面不同，自由曲面结构起伏众多，形状多样，力学性能明显不同于常规曲面.崔昌禹等[5]提出能够实现结构形状与力学性能相互协调统一的高度调整法.崔昌禹等[6]针对自由曲面实际工程进行分析，研究初始缺陷对承载力的影响.Isozaki[7]利用“高度调整法”设计了多项自由曲面结构作品，在设计过程中探讨了力学性能，但只局限于单个工程项目，没有系统的研究.

本文以采用高度调整法优化后的典型正负高斯曲率自由曲面为研究对象，研究内力分布特性、荷载-位移曲线特征与破坏模式、初始缺陷的影响.结合实际工程，系统分析自由曲面结构的力学特性.

1 自由曲面模型数值模拟

1.1 本构方程

采用有限元分析软件ABAQUS塑性损伤模型进行数值模拟.

采用材性受压试验的本构方程[8]：

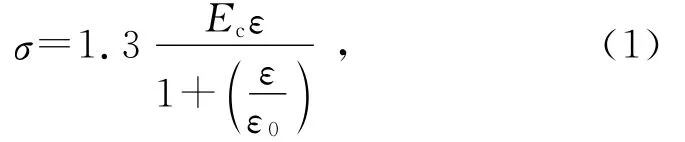
式中：Ec为弹性模量，Ec=2.66×104MPa；fc为立方体抗压强度，fc=39.0 MPa；ε0为峰值应力所对应的应变.

采用Reinhardt等在1985年提出的混凝土受拉应力应变公式[9]：

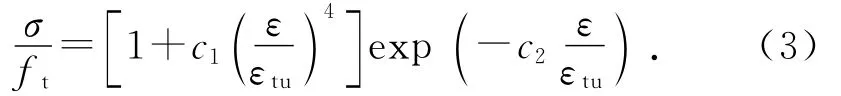
式中：ft为混凝土抗拉强度，ft=3.11 MPa；εtu为混凝土极限拉应变，εtu=0.001；c1、c2为回归系数，本文取c1=9.0，c2=5.0.

1.2 增加收敛手段

混凝土的本构方程复杂，求解混凝土问题时会经常遇到收敛问题，特别是自由曲面形状复杂，网格不容易划分，很容易出现数值奇异现象.采用的收敛手段归纳如下.

1）膨胀角采用30°，黏性系数采用0.000 5，打开Discontinuous analysis.

2）由于混凝土模拟难度较大，可以牺牲一些计算精度来达到收敛的目的，采用江见鲸等[10]的建议对力和位移收敛差放宽到2％～3％.

3）输出单元和积分点在塑性算法中迭代步信息，修改迭代不收敛处网格尺寸的大小，避免网格划分太稀疏或太密集而不收敛的现象.

1.3 试验结果对比

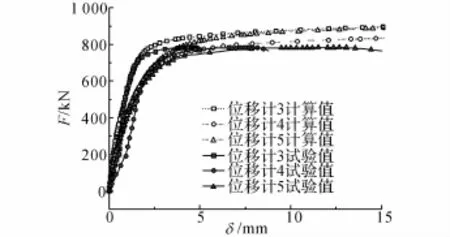
图1 竖向荷载-位移曲线Fig.1 Vertical load-displacement curve

采用文献[8]的自由曲面结构进行有限元分析，本构方程采用前文所述，采用文献[8]材性试验的泊松比ν=0.268.如图1所示为试验值和数值计算值的竖向荷载F-位移δ全过程曲线.可以看出：试验值和数值模拟值的差别较小，弹性段基本重合.结构弹性刚度很大，荷载-位移全过程曲线没有明显下降段，与弹性段相比，结构塑性发展段较长.自由曲面壳实测值的最大荷载为780k N，而对理想自由曲面壳的理论计算结果为870k N，两者相差仅11％.

2 自由曲面结构力学特性分析

尽管自由曲面结构的形式多样，但可以分解为一系列正负高斯曲率曲面.本文选择典型自由曲面Ⅰ、Ⅱ来研究自由曲面的力学特性.

如图2、3所示为典型自由曲面Ⅰ、Ⅱ的侧视图，平面投影均为正方形，边长均为50 m.周边铰接约束，壳体厚度设为0.2 m，材性参数选择1.1节的本构方程.图中，“+”表示正高斯曲率区，“-”表示负高斯曲率区，“+-”表示正负高斯曲率过渡区.

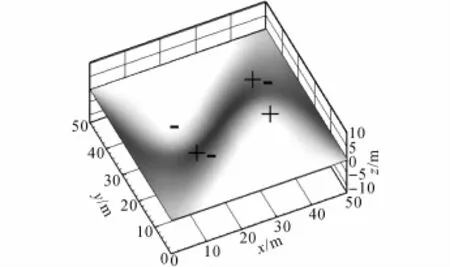
图2 典型自由曲面ⅠFig.2 Typical freeform surface（type I）

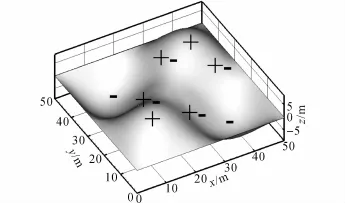
图3 典型自由曲面ⅡFig.3 Typical freeform surface（typeⅡ）

2.1 内力分布特性

图4 模型I内力分布云图Fig.4 Contours of internal force model I

2.1.1 薄膜应力分布特性 通过薄膜第一主应力和第二主应力来表达壳体结构内所产生的薄膜应力分布特性.如图4（a）、5（a）所示分别为模型I、模型II的薄膜第一主应力与其平均值之比.从图4（a）、5（a）可以看出，结构在负高斯曲率区受拉作用大，与其他位置相比，负高斯曲率区两侧边受拉作用更明显.正高斯曲率区次之，而正高斯曲率区两侧边与其他位置相比受拉作用很小.正负高斯曲率过渡区的第一主应力很小，在模型II中此处受压.如图4（b）、5（b）所示分别为模型I、模型II的薄膜第二主应力与其平均值之比.模型I的薄膜第二主应力在正高斯曲率区受压作用大，与其他位置相比，正高斯曲率区两侧边受压作用更明显.在负高斯曲率区受压作用较小，与其他位置相比，负高斯曲率区两侧边受压作用更小（见图4（b））.模型II的薄膜第二主应力在高斯曲率过渡区受压作用最大，正高斯曲率区域次之，负高斯曲率区域与负高斯曲率侧边最小（见图5（b））.结构在正高斯曲率区可以看成拱的作用，大部分受压；在负高斯曲率区可以看成悬索作用，大部分受拉.

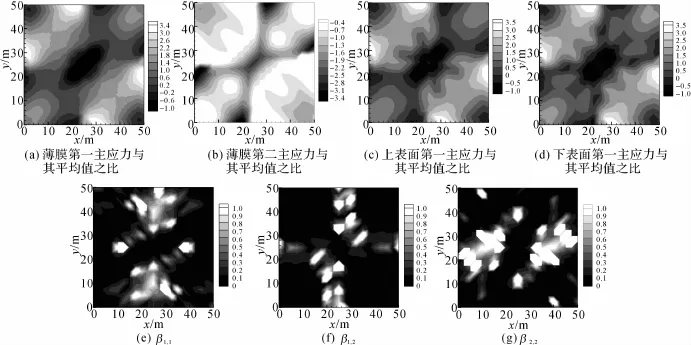
图5 模型II内力分布云图Fig.5 Contours of internal force model II

2.1.2 上、下表面第一主应力分布特性 模型I结构的上、下表面第一主应力在负高斯曲率区都较大，正高斯曲率区域较小，见图4（c）、（d）.下表面第一主应力除正负高斯曲率过渡区外比同位置上表面第一主应力大，高斯曲率过渡区下表面比上表面小，且上、下表面第一主应力分布和薄膜应力分布相近.模型II上、下表面的第一主应力分布模式几乎相同，说明结构受弯作用很小，几乎是纯受拉压结构，见图5（c）、（d）.结构裂缝发生、发展过程与表面第一主应力的分布模式相关，根据上、下表面第一主应力分布特性可以推测裂缝发生过程.

2.1.3 弯曲内力与薄膜内力比分布特性 为了考察弯曲内力在总内力中所占的比重，定义弯曲内力与薄膜内力比：

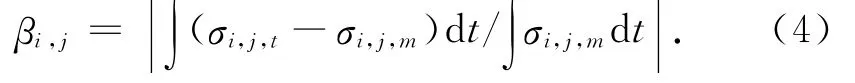
式中：σi，j，t为壳体上表面单元应力，σi，j，m为壳体中心面单元应力.

当i=j=1时，β1，1越大，表示结构x向受弯作用越明显，弯曲内力所占比重越大，结构抵抗荷载的效率越低；反之，则表示结构x向受弯作用越小，弯曲内力所占比重越小，结构抵抗荷载的效率越高.当i=j=2时，表示y向受弯作用；i=1、j=2表示受扭作用.

模型I结构在正、负高斯曲率过渡区弯曲内力与薄膜内力比最大，其他位置很小，见图4（e）～（g）.模型II与模型I的规律相类似，见图5（e）～（g）.正高斯曲率区主要受压，负高斯曲率区主要受拉，因此高斯曲率过渡区为拉压应力过渡区，结构受弯较明显.

2.2 荷载-位移曲线与结构破坏模式

在实际工程设计过程中发现，自由曲面结构的破坏形式以强度破坏为主，且缺陷对承载力的影响很小.利用本文的2种典型正负高斯自由曲面进行分析.

图6、7的均布荷载q-位移曲线没有下降段，结构破坏模式为强度破坏.与弹性段相比，结构塑性发展段较长.结构破坏荷载相对于弹性段荷载相差不大，说明结构可以充分利用材料的强度.荷载位移曲线的特点和文献[7]所得的试验曲线特点相同，结构有很大的刚度，结构在使用荷载作用下，几乎没有变形，可以很好地满足对结构变形和裂缝有很高要求的结构形式.

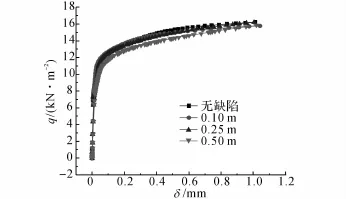
图6 不同缺陷下自由曲面Ⅰ的荷载-位移曲线Fig.6 Load-displacement curves of freeform surface I under different imperfection conditions

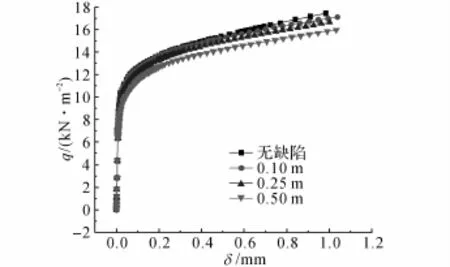
图7 不同缺陷下自由曲面Ⅱ的荷载-位移曲线Fig.7 Load-displacement curves of free-form surfaceⅡunder different imperfection conditions

2.3 初始缺陷的影响

高度调整法是通过调整节点坐标使结构应变能最小.当计算收敛时，节点坐标的微小改变对结构的应变能不产生影响，因此，自由曲面结构对缺陷不敏感.

如图6、7所示分别为结构无缺陷和缺陷为0.1、0.25、0.5 m的荷载-位移全过程曲线，图6、7和图1的荷载-位移曲线规律是相同的，结构对缺陷的影响很小.当缺陷为0.5 m时，模型I和模型II的承载力分别比无缺陷承载力下降6.9％和9.4％.在正常设计和施工中可以不考虑缺陷的影响，这对结构的设计者和施工者来说是非常方便的.

3 工程实例分析

在实际工程中，自由曲面形状更自由多变而且约束条件复杂，因此采用实际工程来验证结构是否发生强度破坏和是否缺陷对结构影响较小.算例采用笔者提出的高度调整法设计和优化的工程实例来验证所提观点.3.1和3.2节算例的材性参数采用1.1节公式且结构承受均布荷载.不同缺陷情况下的荷载-位移全过程分析采用非线性本构方程，内力分布云图分析采用线弹性本构方程.

3.1 北方生涯学习中心

如图8所示为北方生涯学习中心（2002年竣工），平面尺寸为40 m×54 m，壳体厚度为15 cm.

在实际工程中，由于约束条件复杂，不是简单的四周约束，因此分析结构应力时要同时考虑约束条件.如图9（a）所示为薄膜第一主应力与其均值之比的分布云图.薄膜第一主应力在结构负高斯曲率区和约束附近处较大，第二主应力与其平均值之比绝对值在负高斯曲率区和约束附近处较小.在约束A 和H之间较大（见图8（a）），A和H之间为正高斯曲率区，而且两端约束，形成近似拱作用.上、下表面的第一主应力分布模式类似，均与薄膜第一主应力相近，说明上、中、下表面第一主应力分布类似，从侧面说明结构主要受面内应力，弯矩作用较小.弯矩与薄膜内力之比的β1，1、β2，2在约束处较大，β1，2在壳体正高斯曲率区较大.

如图10所示为结构在无缺陷和缺陷为0.1、0.25、0.5 m时的荷载-位移曲线.当缺陷分别为0.1、0.25、0.5 m时，极限荷载分别是无缺陷荷载时的1.8％、2.6％、6.5％，对初始缺陷的影响很小.结构的最大弹性竖向位移约为6.2 cm.

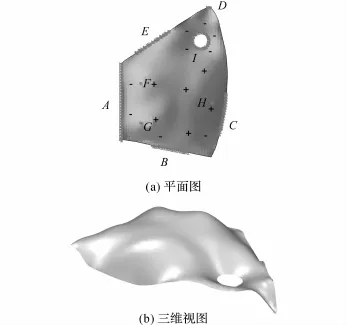
图8 北方生涯学习中心Fig.8 Kitagata community center

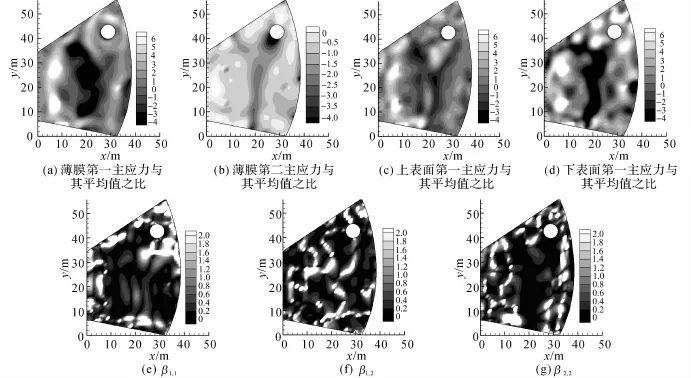
图9 北方生涯学习中心内力分布云图Fig.9 Contours of internal force of Kitagata community center

图10 不同缺陷下的荷载-位移曲线Fig.10 Load-displacement curves under different imperfection conditions

3.2 日本Kakamigahara殡仪馆

如图11所示为日本Kakamigahara殡仪馆（2006年竣工），平面尺寸为77 m×57 m，壳体厚度为15 cm.

如图12（a）所示为薄膜第一主应力与其均值之比的分布云图.薄膜第一主应力在负高斯曲率区较大，约束区E内为正高斯曲率区且四周铰接，相当于四周铰接的拱作用，第一主应力为负值，受压.薄膜第二主应力在负高斯曲率区较小，上、下表面第一主应力规律接近，都与薄膜的第一主应力规律相同.由于存在多个点的铰接约束，弯曲内力与薄膜内力之比的分布规律复杂，但大部分较小.

如图13所示为结构在无缺陷和缺陷为0.1、0.25、0.5 m时的荷载-位移曲线.当缺陷分别为0.1、0.25、0.5 m时，极限荷载分别是无缺陷荷载时的1％、6.7％、11.8％.结构的最大弹性竖向位移约为2.3 cm.

图11 Kakamigahara殡仪馆Fig.11 Crematorium in Kakamigahara

4 结 论

（1）薄膜第一主应力在负高斯曲率区受拉大，正高斯曲率区小；薄膜第二主应力在正高斯曲率区大，负高斯曲率区小；上、下表面第一主应力的分布模型类似；结构在正、负高斯曲率过渡区弯曲内力与薄膜内力比最大，其他位置很小.

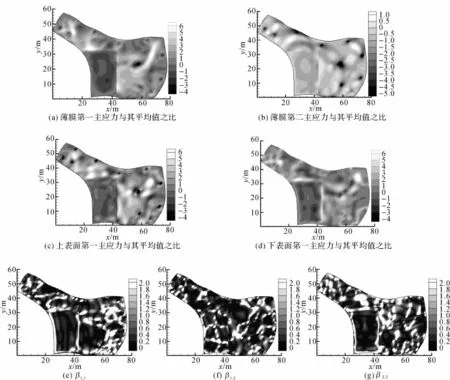
图12 日本Kakamigahara殡仪馆内力云图Fig.12 Contours of internal force of crematorium in Kakamigahara

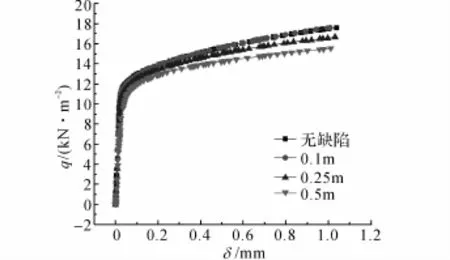
图13 不同缺陷下的荷载-位移曲线Fig.13 Load-displacement curves under different imperfection conditions

（2）自由曲面结构的受力合理、刚度大且有明显的塑形段，荷载-位移曲线没有下降段，破坏模式以强度破坏为主.

（3）自由曲面壳体结构对缺陷很不敏感，在正常施工时，可以完全不考虑缺陷的影响，相比常规壳体更适合大跨空间结构.

（

）：

[1]祝恩淳，沈世钊.钢纤维混凝土圆柱壳稳定性能的试验研究[J].哈尔滨建筑大学学报，1996，29（1）：37-42.

ZHU En-chun，SHEN Shi-zhao.Experiment and study on the stability behaviours of a SFRC cylindrical thin shell[J].Journal of Harbin University of Architecture and Engineering，1996，29（1）：37-42.

[2]唐如意.钢-碳纤维混凝土组合肋壳弹塑性分析[D].西安：西安建筑科技大学，2009：59-72.

TANG Ru-yi.Elastoplasticity analysis of steel-carbon fiber reinforced concrete composite ribbed shell[D].Xi’an：Xi’an University of Architecture and Technology，2009：59-72.

[3]常玉珍.刚-混凝土组合肋壳非线性分析[D].西安：西安建筑科技大学，2007：55-91.CHANG Yu-zhen.Nonlinear analysis of steel-concrete composite ribbed shell[D].Xi’an：Xi’an University of Architecture and Technology，2007：55-91.

[4]何广乾，魏连，车文珍，等.椭圆抛物面双曲扁壳在均匀外压作用下的非线性弹性稳定性[J].土木工程学报，1965，1（1）：1-23.

HE Guang-qian，WEI Lian，CHE Wen-zhen，et al.The nonlinear elastic stability of elliptic paraboloid double-curvature shallow shell under uniform external pressure[J].China Civil Engineering Journal，1965，1（1）：1-23.

[5]崔昌禹，严慧.自由曲面结构形态创构方法：高度调整法的建立与其在工程设计中的应用[J].土木工程学报，2006，39（12）：1-6.

CUI Chang-yu，YAN Hui.A morphosis technique for curved-surface structures of arbitrary geometries：height adjusting method and its engineering applications[J].China Civil Engineering Journal，2006，39（12）：1-6.

[6]崔昌禹，姜宝石，崔国勇.结构形态创构方法的工程应用.[J].建筑钢结构进展，2011，13（6）：9-18.

CUI Chang-yu，JIANG Bao-shi，CUI Guo-yong.Engineering applications of structural morphogenesis methods[J].Progress in Steel Building Structures，2011，13（6）：9-18.

[7]ISOZAKI A.GA Document 77[M].[S.l.]：Yoshio Futagawa，2004.

[8]崔昌禹，崔国勇，姜宝石.自由曲面混凝土壳体结构静力试验研究[J].建筑结构学报，2014，35（11）：68-75.

CUI Chang-yu，CUI Guo-yong，JIANG Bao-shi.Experimental study on static behavior of free-surface concrete shell[J].Journal of Building Structures，2014，35（11）：68-75.

[9]雷拓，钱江，刘成清.混凝土损伤塑性模型应用研究.[J].结构工程师，2008，24（2）：22-27.

LEI Tuo，QIAN Jiang，LIU Cheng-qing.Application of damaged plasticity model for concrete[J].Structural Engineers，2008，24（2）：22-27.

[10]江见鲸，陆新征，叶列平.混凝土结构有限元分析[M].北京：清华大学出版社，2005：47-53.

Mechanical property of free-form surface concrete structure

CUI Guo-yong1，CUI Chang-yu1，2，TU Gui-gang1

（1.School of Civil Engineering，Harbin Institute of Technology，Harbin150090，China；2.Key Laboratory of Structures Dynamic Behavior and Control of China Ministry of Education，Harbin Institute of Technology，Harbin150090，China）

The finite element（FE）model of the free-form surface concrete structure was built using the FE analysis software ABAQUS by rationally selecting the constitute relationship of the concrete in order to study the mechanical properties.The correctness of the FE model was verified compared with the related experiments.Then the distribution characteristic of the internal force of the typical free-form surface structure，load-displacement curves，failure mode and initial imperfection were investigated.Results show that the first principle membrane stress was tensile stress with high value in negative Gauss curvature region while it was tensile stress with small value in positive Gauss curvature region.The second principle membrane stress was compressive stress with high value in positive Gauss curvature region while it was compressive stress with small value in negative Gauss curvature region.The first principle stress of both the top and bottom surface has similar distribution mode.The ratio between bending and membrane internal force is higher in the transition region between the positive and negative Gauss curvature region than the rest region.The loaddisplacement curve has no descent segment，meaning that the failure mode of the structure was strength failure.The initial imperfection has small influence on the structure.The mechanical analysis of two practical projects was performed to verify the correctness of the concluded mechanical properties.

shell structure；shape optimization；ABAQUS；freeform surface

TU 33；TU 311

A

1008-973X（2015）10-1960-07

2014-09-09.浙江大学学报（工学版）网址：www.journals.zju.edu.cn/eng

国家自然科学基金面上项目（50978075）.

崔国勇（1986—），男，博士生，从事自由曲面形状优化与力学性能的研究.ORCID：0000-0002-4147-9949.

E-mail：guoyonghit@163.com

崔昌禹，男，教授，博导.ORCID：0000-0002-4245-7274.E-mail：cuichangyu1963@aliyun.com