系杆拱桥吊杆索力张拉的模型试验研究

邓晓，王起才，张戎令，杨阳

(兰州交通大学土木工程学院，甘肃兰州730070)

系杆拱桥吊杆索力张拉的模型试验研究

邓晓，王起才，张戎令，杨阳

(兰州交通大学土木工程学院，甘肃兰州730070)

钢管混凝土系杆拱桥吊杆索力张拉是系杆拱桥施工的重要步骤。本文结合相似比理论，根据现场实际桥梁模拟浇筑1∶16试验模型，采用有限元分析得出实际桥型与实验室模拟桥型的索力张拉值。通过与兰新铁路第二双线实际桥梁的张拉值对比，得出索力张拉顺序对各个吊杆索力的影响，以及索力在第一次张拉完成后实测值与预期张拉值的相差值，通过实测值反推出系杆拱桥索力张拉初始值。实验室桥梁模型模拟实际桥型进行索力的测定和调整，对现场施工以及对系杆拱桥的调索具有指导意义。

系杆拱桥 相似比理论 有限元模拟 索力张拉

钢管混凝土系杆拱桥是无推力拱，受力明确，一般为外部静定，内部超静定结构［1-2］，其强度高、塑性好、质量轻，具有很高的抗压强度和抗变形能力。因此，此类桥梁结构形式被广泛应用到我国的桥梁建设当中［3］。桥面纵横梁的荷载通过吊杆传递到拱肋上，所以设计中确定系杆拱桥吊杆的索力张拉值，施工中对拱桥吊杆的索力张拉是整个钢管混凝土系杆拱桥施工的关键问题之一［4］。如何控制和调整吊杆初始张拉力，保证在桥梁成型后吊杆的索力值能够达到预期张拉值是吊杆设计以及施工中比较棘手的问题。同时，在桥梁的施工监控中，拱桥吊杆索力的监控也是其重要内容，对于整个施工进度以及成桥有很大的影响［5］。在一些系杆拱桥的加固维修，以及吊杆的更换当中，索力测试也是其中的重要步骤。因此对系杆拱桥的索力测试进行实验室模拟研究十分必要，同时也为钢管混凝土系杆拱桥的系统研究提供了重要依据和保障。

1 测试方法

目前应用在系杆拱桥吊杆索力测试的主要方法有压力传感器法、油压千斤顶法、磁通量法、有限元分析法、振动频率法等［6］。由于振动频率法不需要预埋传感器，它利用环境的随机振动或人工激振作为吊杆激振，在吊杆上附着高灵敏度的传感器，拾取吊杆在环境激励下的振动信号，经过滤波、放大、谱分析，测定结构的振动特性。然后，根据吊杆索力与其振动频率之间的关系求出吊杆的索力。因此，对于成桥索力测试一般都采用振动频率法。

测定吊杆索力张拉值采用S形受拉式传感器，连接DH-3818静态应变测试系统，通过此系统读出对应吊杆的应变值，通过应变值换算出其相应的索力张拉值［7-8］。

2 工程概况

乌鲁木齐河特大桥DK1831+562.29—DK1831+ 692.39段跨越河滩路(图1)，为双线铁路桥，是兰新铁路第二双线的重点工程。主桥位于竖曲线内，实际纵坡20%，设计中按正做斜置，即吊杆垂直于梁体。平面位于R=2 800 m的圆曲线上，按直线梁设计，平面采用平分中矢布置，梁端外矢距为38 cm，跨中外矢距为37.25 cm。

图1 乌鲁木齐河钢管混凝土系杆拱桥

主桥上部结构采用1孔128 m简支系杆拱，拱轴线采用二次抛物线。横桥向设置两道拱肋，拱肋中心间距为13.8 m。系梁采用预应力混凝土简支箱梁，采用单箱双室截面，结构设计为刚性系梁刚性拱。两道拱肋共设17对吊杆，第一对吊杆距支点14.4 m，其余吊杆中心间距均为6.2 m。该桥在施工中的索力张拉是整个桥梁成型的重要问题之一，所以实验室浇筑相应比例模型，为吊杆张拉力以及张拉顺序的确定提供依据。

3 吊杆索力测试

在结构模型试验研究中，只有模型和原型保持一定的相似比，才能由模型试验结果推算出原型结构的相应结果。结合相似比理论根据实际桥梁结构，确定在实验室模拟浇筑1∶16的桥梁模型。

由于实际桥型为刚性系杆刚性拱，所以为了更结合实际，实验室也模拟浇筑为刚性系杆刚性拱。试验所采用吊杆是直径为0.8 cm的钢绞线，采用这种钢绞线也是为了在切合度上达到试验所要求的精度。本试验在吊杆张拉过程中，先进行钢丝束的下料，然后进行编束，将钢丝的一段锚固于拱肋之上，然后将另一头的钢绞线穿过梁体孔道，在梁体下采用锚具在施加预期张拉力之后进行锚固。

在试验初期先对每个吊杆上布置的受拉传感器进行标定，标定采用电子万能试验机以及DH-3818静态应变测试系统。每5 kN为一级对传感器进行加载，每级对应一个应变值，这样可以对应拟合出一个传感器标定曲线，从而通过DH-3818所显示的应变值就可以确定相应的索力张拉值。图2为受拉传感器标定曲线。

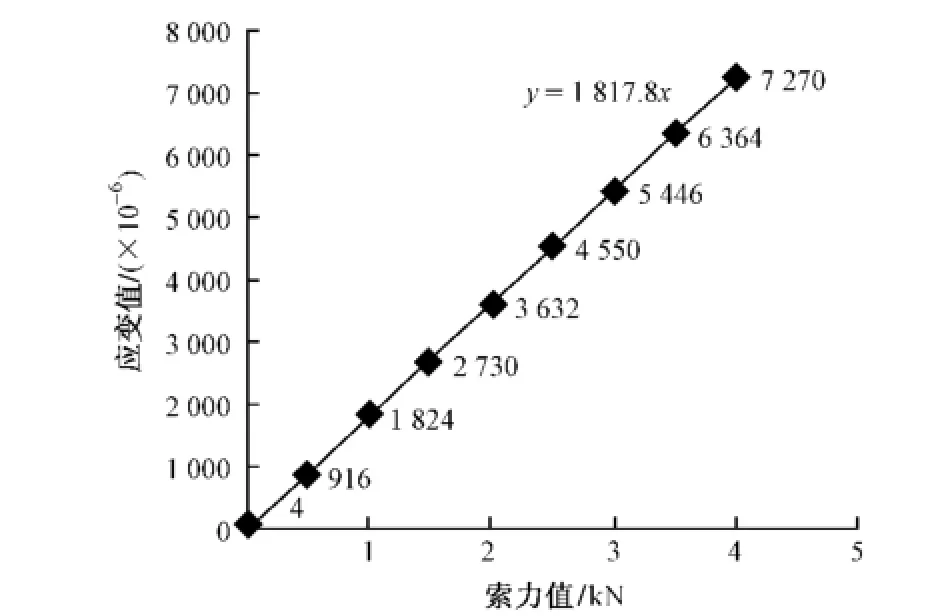
图2 受拉传感器标定拟合曲线

为方便研究，对吊杆进行A，B编号，每侧17对吊杆，由小里程往大里程编号为1～17。张拉通常按序(从拱顶向拱端或从拱端向拱顶)对称地进行。整个桥梁的张拉顺序为5B13A-5A13B-1B17A-1A17B-9B9A-3B15A-3A15B-7B11A-7A11B-2B16A-2A16B-8B10A-8A10B-4B14A-4A14B-6B12A-6A12B，很显然，对于同一最终预张拉力的设计值，不同的吊杆张拉顺序，在各吊杆中施加的初始张拉力大小是不同的。而系梁的刚度较大时，吊杆索力将对结构内力、变形和刚度产生很大的影响，不良的索力将降低结构运营安全性和可靠度［4］。吊杆索力张拉值按照相似比原理换算的模型索力张拉值如表1所示。

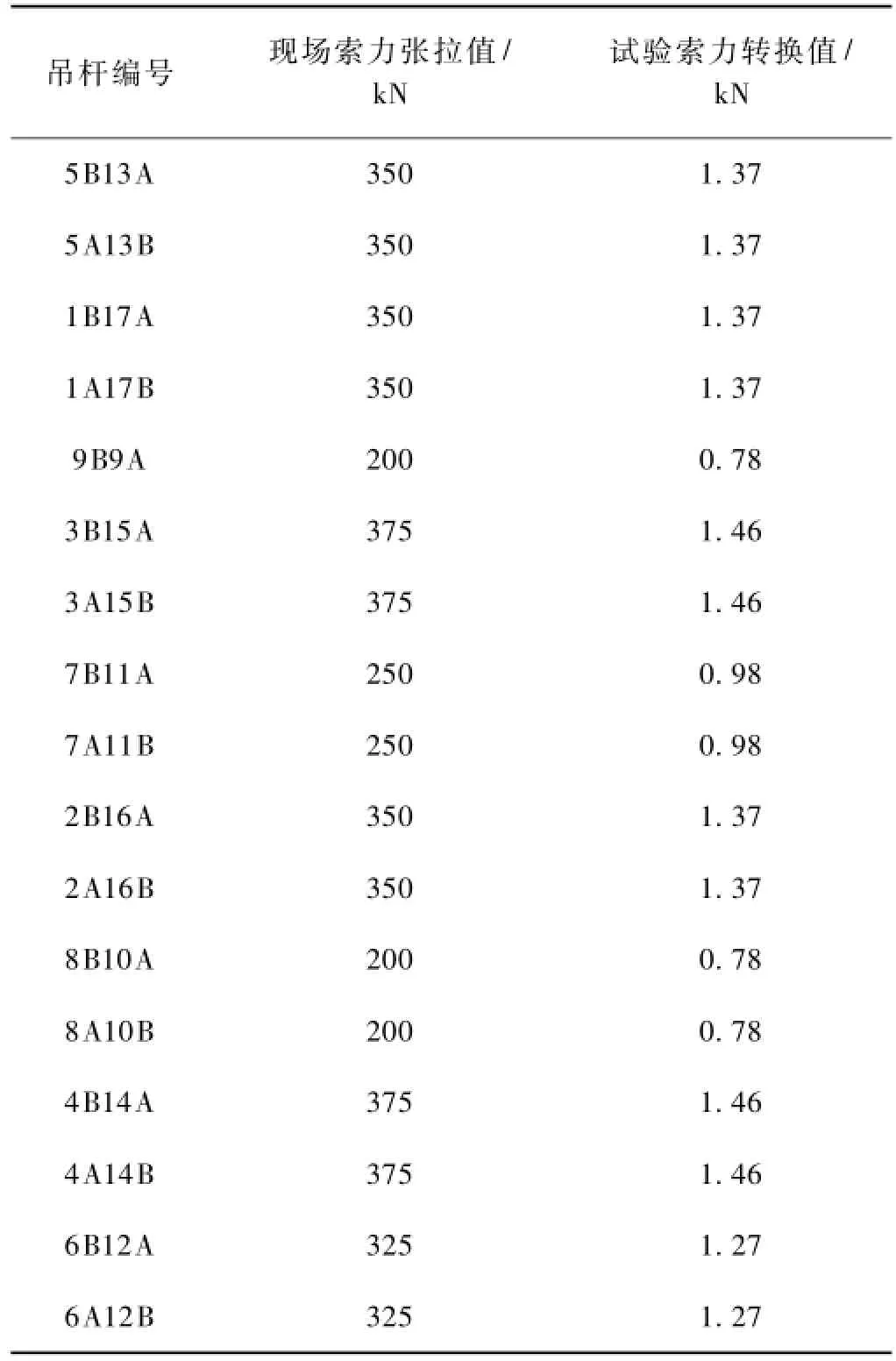
表1 索力张拉初始值及转换值

在试验的过程中，后一根吊杆的张拉总会对前面所张拉的吊杆的索力张拉值产生影响。并且模型与实际结构还存在一定的差异，以及在吊杆张拉过程当中人为操作因素和测量计算误差等的影响，实际张拉完成后与预期要达到的目标值还有一定的差距。为了满足精度要求，要进行索力的调整。在所有吊杆索力张拉完成后可测出每根索力的实际张拉值，通过对比实测值与目标张拉值可以很好地调整索力初始张拉值。通过试验研究调整得出的系杆拱桥初始索力张拉值，可以很好地指导现场施工时的索力张拉。具体调整值如表2所示。

表2 试验吊杆索力调整值

4 结论

通过实验室浇筑1∶16钢管混凝土系杆拱桥模型，结合有限元模拟，得出吊杆的索力初始张拉值，对每根吊杆施加初始张拉力。当每根吊杆索力张拉完成后，重新测试索力张拉值，通过分析目标值与预期值，得出在吊杆的张拉过程中，后一根吊杆的张拉都会对前面所有吊杆初始的张拉值产生影响。同时可以看出系杆拱桥的索力张拉过程比较复杂，张拉顺序以及张拉值对拱桥的成桥都有很大的影响，所以合理地确定吊杆索力值极为重要。在拱桥施工或者试验中吊杆索力对系杆拱桥的安全性、适用性和可靠度有很大的影响，而且由于张拉吊杆时索力复杂的相互影响，张拉控制力的确定也是一个难点。故此试验可以很方便地确定吊杆多次、分批张拉问题，保证张拉完成时即可达到设计要求。

［1］范立础.桥梁工程(上册)［M］.北京:人民交通出版社，2001:1-17.

［2］李杰，陈淮，江莹莹，等.钢管混凝土系杆拱桥吊杆力计算及调索方法研究［J］.铁道建筑，2014(1):7-10.

［3］顾安邦.桥梁工程(下册)［M］.北京:人民交通出版社，2000:1-14.

［4］于琦，孟少平.系杆拱桥吊杆张拉控制有限元模拟方法研究［J］.特种结构，2008，25(1):89-91.

［5］赵洋，李树山，李晓克，等.系杆拱桥吊杆索力测试研究［J］.工程抗震和加固改造，2011，33(4):56-60.

［6］魏建东.索力测试常用公式精度分析［J］.公路交通科技，2004，21(2):53-56.

［7］彭宣茂.系杆拱桥吊杆初始张拉力的计算方法［J］.水利水电科技进展，2000，20(6):32-34.

［8］孙九春.拱式结构吊杆张拉索力计算方法综述［J］.结构工程师，2010，26(4):154-159.

Experimental study on cable tension of tied arch bridge model

DENG Xiao，WANG Qicai，ZHANG Rongling，YANG Yang
(School of Civil Engineering，Lanzhou Jiaotong University，Lanzhou Gansu 730070，China)

Cable tension of CFST(concrete filled steel tube)tied arch bridge is a key step in construction.Sim ilarity ratio theory and m odel test w ere introduced in this paper.T he ratio o f the m odel to the real structu re w as 1/16.Finite element method was applied to analyze the cable tension in both the model and the structure.W ith comparison to the cable tension in the bridge in the second double line of Lanx in Railw ay，the effect of the tension order on the tension in each suspender w as analyzed.T he tension(after the first tension)d ifference between the pred icted and the m easu red was calcu lated，and the initial tension was calcu lated based on the m easured value.T he m odel test was perform ed，sim ulating the real structu re.T he cab le tension of the m odel w as m easu red and ad justed，contributing to the construction of the real structure.

T ied arch bridge;Sim ilarity ratio theory;Finite elem ent sim ulation;Cable tension

U448.22+5

A

10.3969/j.issn.1003-1995.2015.06.05

1003-1995(2015)06-0017-03

(责任审编赵其文)

2014-09-27;

2015-03-12

长江学者和创新团队发展计划项目(IRT1139);国家自然科学基金资助项目(51268032);兰州交通大学青年科技基金项目(2012028)

邓晓(1991—)，男，甘肃庆阳人，硕士研究生。