基于聚类小生境遗传算法的DNA编码优化
郑学东
(大连大学先进设计与智能计算省部共建教育部重点实验室,辽宁大连116622)
基于聚类小生境遗传算法的DNA编码优化
郑学东
(大连大学先进设计与智能计算省部共建教育部重点实验室,辽宁大连116622)
DNA编码优化问题是DNA计算中的核心问题。分析DNA编码优化的约束条件,在单链DNA序列集合上引入h距离,将聚类小生境技术应用于小种群遗传算法的构造,对DNA编码优化问题进行求解。基于h距离定义DNA序列间的相似函数,将碱基字母编码为4进制整数、DNA编码序列作为个体编码为4进制整数向量、种群编码为4进制整数矩阵,基于模4算术运算,构造相应的遗传算子,并给出DNA编码序列的具体计算结果。实验结果表明,与现有DNA编码序列优化结果相比,该算法可得到更好的DNA编码序列且计算效率较高。
DNA计算;DNA编码;遗传算法;聚类分析;小生境;模运算
1 概述
DNA编码问题是DNA计算[1-2]研究中的首要与核心问题[3]。在DNA编码问题中,首要目标是提高DNA编码序列的特异性识别能力,即降低DNA序列间的相似性。文献[4]提出用最小相同子序列来定义不同DNA编码序列之间的相似程度。由于DNA分子在溶液中可以自由扩散与相对移动,文献[5]提出用移位测度(h-measure)来刻画DNA编码序列之间的相似性。尽管移位测度不满足距离公理,但由于考虑了在DNA序列间可能发生的移位杂交,因此其仍是一个度量DNA序列间相似程度的较好方法。Phan等人于2009年基于移位测度进一步定义了h距离(h-distance)[6],并对相应距离空间的几何性质进行了讨论,给出了DNA序列集合设计的相应结果。由于DNA分子具有特殊的理化性质,为了保证参与生化反应的DNA分子具有一致的理化性质,在DNA编码过程中还需考虑其他诸如自由能、解链温度、连续性、GC含量等DNA分子的热力学约束以及发卡等二级结构约束[7]。
上述相关约束大致可以分为2类:一类是汉明距离类约束(或称为组合类约束,约束条件主要基于汉明距离定义,如相似性与移位测度),这类约束的主要目标是增加DNA分子的特异性识别能力,避免出现假阳性或假阴性的错误配对;另一类是热力学约束及二级结构类约束,这类约束的主要目标是保证DNA分子理化性质的稳定性与一致性,以保证生化反应的顺利进行。
对于DNA编码问题,求解方法主要有随机搜索[8]、进化算法[9-10]、模板映射方法[11]、多目标优化[12-13]等。DNA编码问题是一个难于求解的问题[14],目前还没有统一的规范方法来求解。
聚类分析方法作为一种数据分析手段,已在模式识别、数据挖掘等方面得到了广泛应用[15]。本文利用聚类小生境技术,在单链DNA序列集合上引入h距离,定义单链DNA序列间的相似性度量函数,采用小种群遗传算法,基于模4算术运算,设计3个遗传算子,对DNA编码问题进行求解,并给出具体的DNA编码序列。
2 DNA编码的相关约束与优化模型
2.1 约束条件
本文采用的相关约束具体如下:
(1)相似性(Sm):对长度为n的2个DNA序列Dj与Dk,其相似性度量的数学定义为:

(2)移位测度(HM):在考虑相对移动的情况下,为避免2个DNA编码序列之间的杂交,引入hmeasure,其数学定义为:

(3)GC含量(GC):即碱基G与C在DNA序列中的百分比,GC含量约束可表示为:

其中,GC(Dj)表示序列Dj的GC含量;GCgoal表示GC含量的目标值;kGC表示可接受范围。
(4)连续性(Con):在DNA序列中,如果相同碱基连续重复出现,则其生化反应将难以控制,在序列设计中要尽量避免相同碱基的连续出现。连续性约束可表示为:

(5)发卡(Hp):DNA序列可能发生自杂交,并形成环状结构,一般发卡结构是希望避免的。一个DNA分子可能出现的发卡数量可以通过以下公式进行估计:

其中,Hp(p,r,s,Dj)表示在序列Dj中,开始于位置p,环长为r,茎长为s的发卡数。令KHp表示发卡数量的可接受范围,则发卡约束可表示为:

(6)解链温度(Tm):即在DNA变性过程中, 50%的DNA双链变成单链时的温度,其计算可采用最近邻模型[16]。令Tm(Dj)表示序列Dj的Tm值,Tmgoal表示Tm的目标值,kTm表示可接受的Tm值范围,则Tm约束可表示为:

在上述约束条件中,相似性约束与移位测度约束反映了DNA序列及其逆补序列之间公共子序列的共享程度,反映了DNA编码序列之间的相互关系;其他热力学与二级结构类约束则为施加于DNA序列自身的约束,是一种个体约束,反映了DNA编码序列自身的性质。另外,Gibbs自由能可以通过其他约束的组合来替代,因此,这里不考虑Gibbs自由能约束[12]。
2.2 优化模型
由于DNA分子在溶液中可以相对移动与自由扩散,对于编码序列集合C,DNA序列的特异性识别能力取决于彼此间的最小相似性,DNA编码序列间发生错误杂交的可能性取决于彼此间的最小移位测度,因此这里分别取集合C中序列的相似性与移位测度的最小值作为目标函数,其定义为:

将连续性约束fCon(Dj)、发卡约束fHp(Dj)、GC含量约束fGC(Dj)与Tm值约束fTm(Dj)作为优化模型的约束条件。
于是,DNA编码问题可以转化寻找DNA序列集合C⊂{A,C,G,T}∗,使得对∀Dj∈C,满足如下的最大值多目标优化问题:
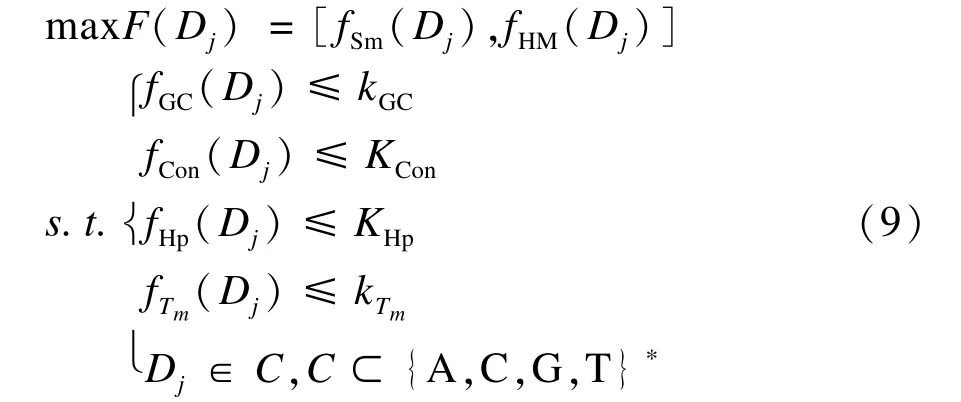
3 本文算法设计


上述定义在DNA双链集合中引入了h距离,使其成为距离空间。尽管h距离定义于双链DNA集合上,但若将DNA序列及其逆补序列视为由单链DNA序列构成的等价类,则可以将h距离引入到单链DNA集合。对于序列Dj与Dk,定义单链DNA序列的h距离为:

其中,hd同时反映了序列Dj与Dk在相似性与移位测度2个度量方面的相似程度。
本文将式(11)作为DNA序列间的相似性度量,利用基于聚类小生境的小种群遗传算法,对优化模型式(9)进行求解。一般在基于进化算法或多目标优化的DNA编码问题求解方法中[9-10,12-13],大多将编码集合C作为个体,即将DNA编码序列连接后作为个体,本文直接将DNA编码序列作为种群个体,个体编码采用4进制整数,即将碱基{A,C,G,T}编码为{0,1,2,3},则DNA编码序列可以视为一个4元码,遗传算法的种群编码为4进制整数矩阵Pm×n,其中,n表示个体长度;m表示种群规模,算法输出Pm×n的子式CM×n作为DNA编码的结果,M表示DNA编码序列的数量,同时也是聚类过程中分类的个数。
个体适应度函数为优化模型式(9)中目标函数与约束条件的线性组合,定义如下:

其中,fi∈{fSm,fHM,-fGC,-fCon,-fHp,-fTm};αi为权重系数。
在遗传算法中采用如下遗传算子:
(1)模交叉算子(Modular Arithmetic Crossover Operator,MAXO):以概率pMAXO随机选择Pm×n的两行作为父代个体,通过模4的加法与减法得到2个子代个体。
(2)多点交叉算子(MultipointCrossover Operator,MXO):以概率pMXO随机选择Pm×n的两行,随机选择l个位点进行交叉。
(3)子式变异算子(Minor Mutation Operator, MMO):以概率pMMO随机选择Pm×n的子式,将其上整数值随机替换为其余碱基对应的整数值。
(4)逆密码子变异算子(Reverse Codon Mutation Operator,RMO):令密码子长度为r,以概率pRMO随机选择Pm×n的k×r级子式,将k×r级子式按行翻转。
(5)逆补密码子变异算子(Reverse Complementary Codon Mutation Operator,RCMO):令密码子长度为r,以概率pRCMO随机选择Pm×n的k×r级子式,将对应整数值按模4取补后再按行翻转。
(6)选择算子(Selection Operator,SO):为降低选择误差,采用无回放余数随机选择法(Remainder Stochastic Sampling with Replacement,RSSR)[17]。
算法终止条件为连续进化500代后停止。算法流程如图1所示。为了扩大算法搜索空间,在算法执行过程使用种群膨胀,膨胀规模至多为初始种群规模的5倍。

图1 小种群遗传算法流程
在一般基于进化计算的DNA编码问题求解方法中,大多将C作为个体,若采用同样的编码方式,
则其种群编码为m×(n×M)阶矩阵Pm×(n×M),其存储复杂度大致为小种群遗传算法的M倍。衡量进化算法复杂度的一种方式是考察每代种群中适应度函数的计算次数及其计算复杂度,在上述算法中,适应度的计算复杂度主要来自于Sm与HM这2个约束条件的计算,对于包含m个个体的种群,每个个体Sm与HM的计算次数为m2,因此在每一代种群中应用适应度进行个体评估时的计算复杂度可以视为O(m3)。
4 实验结果与比较
本文算法用Matlab语言实现,算法参数设置如表1所示,DNA序列的Tm值计算采用Matlab中Bioinformatics Toolbox中的相应函数。

表1 算法参数设置
理论上,相似性与移位测度的值越大,则DNA序列之间发生错误杂交的可能性越低;GC含量与Tm值的分布越集中、连续性值越低,则DNA序列理化性质的一致性越好;发卡的值越低则DNA序列出现二级结构的可能性越低。基于上述考虑,提出以下DNA编码评估标准:选择编码序列集合的最小相似性(minSm)与最小移位测度(minHM)作为评估项,以反映DNA编码序列的特异性识别能力;选择GC含量与Tm值的标准差(σ(GC),σ(Tm)),选择发卡与连续性的和(sumCon,sumHp)作为评估项,以反映DNA分子理化性质的一致性。为说明算法的有效性,将实验结果与目前最新的DNA编码优化结果——文献[13]中的结果进行比较,比较结果如表2~表7所示,编码评估项的比较如图2~图4所示。

表2 文献[13]中长度为20的7个DNA编码结果

表3 本文长度为20的7个DNA编码结果
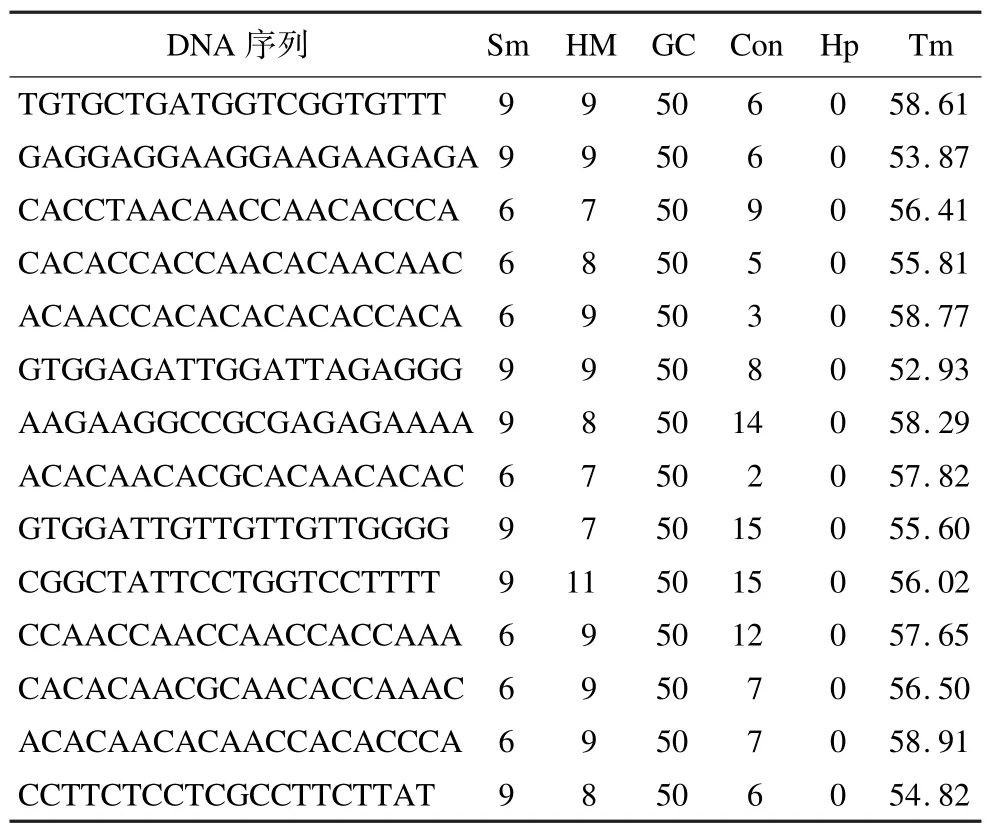
表4 文献[13]中长度为20的14个DNA编码结果

表5 本文长度为20的14个DNA编码结果

表6 文献[13]中长度为15的20个DNA编码结果

表7 本文长度为15的20个DNA编码结果

图2 长度为20的7个DNA编码评估项比较
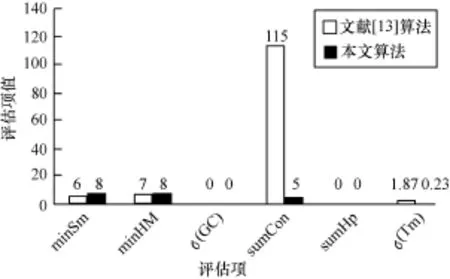
图3 长度为20的14个DNA编码评估项比较

图4 长度为15的20个DNA编码评估项比较
由上述比较结果可知,在所有的评估项上,本文算法均可以获得更好的解,尤其是在连续性方面可以获得较大改善,且序列Tm值与GC含量分布更为集中,说明DNA序列理化性质具有更好的一致性,由于DNA序列的长度较短,因此2种算法在发卡评估项上的结果相同。
在文献[13]中种群规模为3 000,本文算法的初始种群在3种编码情形中分别为20,30,60,考虑到算法运行过程中的种群膨胀,种群规模至多为100, 150,300,另外,文献[13]中的种群个体对应为一个DNA编码集合,即M个长度为n的DNA序列的连接为一个个体,本文种群个体仅为一个长度为n的DNA序列,因此本文算法的计算量要小得多,计算效率更好。
5 结束语
本文基于聚类小生境技术,利用小种群遗传算法求解DNA编码问题。小种群遗传算法的成功应用说明了DNA编码问题可以视为一个多模函数的优化问题。在一般聚类分析中,类的个数是一个难于预先确定的量,由于DNA编码中已确定需要的DNA编码序列数量,因此聚类过程中类的个数是预先选定的。如果不预先指定类的个数,则可以预期在同等约束条件下得到更多的DNA编码序列。今后将结合局部搜索方法及自适应方法,进一步提高DNA编码问题求解的效率。
[1] Adleman L.MolecularComputationofSolutionto Combinatorial Problems[J].Science,1994,266(5187): 1021-1023.
[2] Ignatova Z,Martinez-Perez I,Zimmermann K H.DNA计算模型[M].郗 方,王淑栋,强小利,译.北京:清华大学出版社,2010.
[3] Garzon M H,DeatonRJ.CodewordDesignand Information Encoding in DNA Ensembles[J].Natural Computing,2004,3(3):253-292.
[4] Baum E B.DNA Sequences Useful for Computation: USA,EP0772135A1[P].1997-05-07.
[5] Garzon M,Neathery P,Deaton R J,et al.A New Metric for DNA Computing[C]//Proceedings of the 2nd Annual Genetic Programming Conference.San Francisco,USA: Morgan Kaufmann,1997:472-487.
[6] Phan V,Garzon M.On Codeword Design in Metric DNA Spaces[J].Natural Computing,2009,8(3):571-588.
[7] Sager J,Stefanovic D.Designing Nucleotide Sequences for Computation:A Survey of Constraints[C]//Proceedings of the11th InternationalMeeting on DNA Computing. London,UK:Springer-Verlag,2006:275-289.
[8] Penchovsk Y R,Ackermann J.DNA Library Design for Molecular Computation[J].Journal of Computational Biology,2003,10(2):215-229.
[9] Wang Wei,Zheng Xuedong,Zhang Qiang,et al.The Optimization of DNA Encoding Based on GA/SA Algorithm[J].Progress in Natural Science,2007,17(6):739-744.
[10] 张 强,王 宾,张 锐,等.基于动态遗传算法的DNA序列集合设计[J].计算机学报,2008,31(12):2193-2199.
[11] 王向红,刘文斌,朱翔鸥,等.DNA计算中的单模板编码方法改进研究[J].电子学报,2009,37(12): 2720-2724.
[12] Shin S Y,LeeIH,KimD,etal.Multiobjective EvolutionaryOptimizationofDNASequencesfor Reliable DNA Computing[J].IEEE Transactions on Evolutionary Computation,2005,9(2):143-158.
[13] Chaves-González J M,Vega-RodríguezMA.DNA Strand Generation for DNA Computing by Using a Multi-objective Differential Evolution Algorithm[J]. BioSystems,2014,116:49-64.
[14] 张 凯,耿修堂,肖建华,等.DNA编码问题及其复杂性研究[J].计算机应用研究,2008,25(11):3264-3267.
[15] Pedrycz W.基于知识的聚类:从数据到信息粒[M].于福生,译.北京:北京师范大学出版社,2008.
[16] Santalucia J J R,Hicks D.The Thermodynamics of DNA Structural Motifs[J].Annual Review of Biophysics and Biomolecular Structure,2004,33:415-440.
[17] 周 明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,1999.
编辑 陆燕菲
Optimization of DNA Coding Based on Clustering Niche Genetic Algorithm
ZHENG Xuedong
(Key Laboratory of Advanced Design and Intelligent Computing,Ministry of Education,Dalian University,Dlian116622,China)
The optimization of DNA coding plays an important role in DNA computing.In this paper,the constraints of the optimization of DNA coding are described,an h distance is introduced over the set of single DNA strands and a clustering-based niche technique is applied to construct the micro-genetic algorithm which is used to solve the problem of the optimization of DNA coding.In the algorithm,a similarity function between different DNA sequences is defined based on the h distance.The base letters are encoded by quaternary integers,the DNA coding sequences are encoded by the vector of quaternary integers as individuals and the population is encoded by the matrix of quaternary integers.Several genetic operators are constructed based on modulo 4 arithmetic operation and the concrete computing results are presented.Experimental results show that compared with the latest results,the algorithm can get better DNA coding sequences and improve the efficiency of computation.
DNA computing;DNA coding;genetic algorithm;clustering analysis;niche;modular operation
郑学东.基于聚类小生境遗传算法的DNA编码优化[J].计算机工程,2015,41(2):135-140.
英文引用格式:Zheng Xuedong.Optimization of DNA Coding Based on Clustering Niche Genetic Algorithm[J]. Computer Engineering,2015,41(2):135-140.
1000-3428(2015)02-0135-06
:A
:TP301.6
10.3969/j.issn.1000-3428.2015.02.026
国家自然科学基金资助项目(31170797,31370778,61103057,61370005);辽宁省教育厅科研基金资助项目(L2011218);长江学者和创新团队发展计划基金资助项目(IRT1109)。
郑学东(1977-),男,讲师、博士,主研方向:DNA计算。
2014-01-28
:2014-04-03E-mail:xuedongzheng@163.com

