一种提高稀疏观测数据区反演精度的策略

杨克思，朱培民，赵 娜，徐 阳

（1.中国石油吉林油田分公司a.地球物理勘探研究院，b.新民采油厂工艺所，松原 138000；2.中国地质大学 地球物理与空间信息学院，武汉 430074）

YANG Ke－si1a，ZHU Pei－min2，ZHAO Na2，XU Yang1b

（1.Jilin Oilfield Branch，PetroChina a.Geophysical Exploration Research Institute，b.Xinmin Oil Production Factory，Songyuan 138000，China；2.China University of Geosciences，Institute of Geophysics and Geomatics，Wuhan 430074，China）

一种提高稀疏观测数据区反演精度的策略

杨克思1a，朱培民2，赵 娜2，徐 阳1b

（1.中国石油吉林油田分公司a.地球物理勘探研究院，b.新民采油厂工艺所，松原 138000；2.中国地质大学 地球物理与空间信息学院，武汉 430074）

在一个观测数据稀疏的地区，仅用观测数据来获得接近于真实的模型解是非常困难的，因此在反演时加入先验信息，考虑基于参考模型的反演方法是合理的。在一个观测数据有限，先验信息也很少的区域，获取合适的参考模型非常困难。在无法选取合适参考模型的情况下，提出了一种在参考模型远离真实模型的情况下，通过反演迭代过程中对参考模型的不断修改，使参考模型逐步逼近真实模型，从而提高了反演精度的策略。这里设计了均匀层状模型及含异常体的模型对算法进行了验证，证实了此方法对反演大型地质异常体具有较好的适用性。

反演；天然地震层析成像；稀疏观测数据；模型修改方法

0 引言

在一个稀疏观测数据区，其反演问题往往是欠定问题，因此在反演过程中，不能获得唯一的反演结果。为了解决这一问题，可以考虑基于模型的反演，对模型施加合理的约束条件（例如让模型长度‖m‖2最小）。但模型长度最小并不是一个最好的度量（例如解有关海洋中密度扰动的反演问题，就不能找到一个模型长度最小的解），而选择一个参考模型m0，使要求解的模型与参考模型的差距‖mm0‖2最小，会更合理一些，这就是基于参考模型的反演［1］。

基于参考模型的反演需要给定一个合适的参考模型，而参考模型选择的适当与否，关系到反演结果的好坏及迭代的效率。如果参考模型选择的不适当，可能会使迭代次数增多，甚至收敛到一个与真实模型相差很大的反演结果。

给定参考模型的方法很多，常见的方法有两种：①人工给出一个均匀模型［2］；②根据目标区现有的相关资料，通过适当的处理给出一个比较粗略的参考模型。第一种方法简单易行，但给出的参考模型随意性很大，有可能造成算法收敛缓慢甚至不收敛；第二种方法合理可靠，但在数据稀疏、噪声较大的情况下或调查的初期阶段，仍无法得到合适的参考模型。

在无法选取合适参考模型的情况下，作者提出了一种在参考模型远离真实模型的情况下，通过反演迭代过程中对参考模型的不断修改，使参考模型逐步逼近真实模型，从而提高反演精度的策略。这种方法的主要思想，是将每次迭代反演后的结果进行处理，作为下次迭代的参考模型，并将最后输出的参考模型作为反演结果。

以天然地震层析成像为例，作者设计了三个理论模型对算法进行了验证，证实这种反演策略在参考模型与真实模型相差较远的情况下，对于反演较大型的地质构造有较好的适用性。

1 原理

在数据稀疏的情况下，获得合理的反演结果，选用了如下的目标函数［3］：

其中：m代表需要反演求解的模型向量：Ψ（m）为数据拟合项；Φ（m）为基于参考模型的模型约束项；Ω（m）为对模型进行光滑约束的项，其中Φ（m）和Ω（m）的作用主要是正则化；ε和η分别代表阻尼因子和光滑因子，其作用是平衡Ψ（m）、Φ（m）和Ω（m）对目标函数S（m）的贡献，以使得反演过程能够稳定进行，并获得较为理想的模型解。

采用上述的目标函数，其作用可以总结为两点：①在观测数据少、观测系统无法完全覆盖或观测系统布置不合理的情况下，解决反演中的多解问题，获得唯一的确定解；②加入了正则化项，可以解决反演过程中的不稳定性。

若数据d与模型之间的关系为d＝g（m），式（1）中的第一项Ψ（m）具体形式为式（2）：

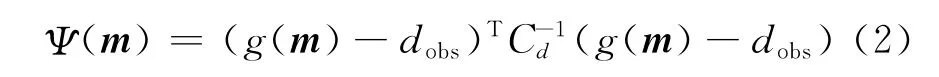
其中：dobs为观测数据；第二项Φ（m）为模型约束项，形式为式（3）。

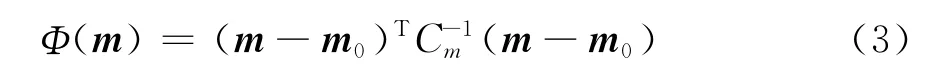
Φ（m）的作用是促使模型解m逼近于参考模型m0，在反演问题是欠定或混定问题的情况下，获得唯一的确定解。由于各模型参数对数据的敏感程度不同，需要用一个权矩阵（模型协方差）Cm平衡每个模型参数误差对预测总误差Φ（m）的贡献，起到对每个模型参数加权的作用。

目标函数中最后一项的作用是定义模型参数之间的关系，以获得最平滑模型解。此项的形式为式（4）。

其中：Dm是一个特定空间导数的有限差分估计；D是二阶导数算子，因此模型越圆滑，Ω（m）会越小。

作者在使用阻尼最小二乘算法进行理论模型反演时发现，当参考模型选取合理时，迭代后的反演结果会逐渐趋近于真实模型。基于这样的考虑，在无法获取合适的参考模型的情况下，将每次迭代后的结果经过处理作为下次迭代的参考模型，经过多次迭代后，可以获取比较合适的参考模型，从而提高了反演的可靠性。图1为参考模型逐步逼近真实模型的反演策略流程图。在图1中，“反演结果处理”项的目的是对当前的反演结果进行适当的处理，从而获取新的参考模型。

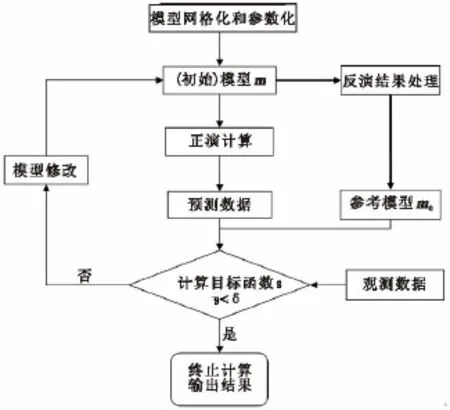
图1 参考模型逐步逼近真实模型的反演策略流程Fig.1 Illustration of the inversion strategy to encourage reference model near to real model step by step

用反演结果估计参考模型的方法可以很多，其基本原则是在反演的最初阶段，新的参考模型应该是整个模型的背景场，而在反演的最后阶段，参考模型应该逐渐接近真实模型。基于上述原则，可以对反演结果进行多尺度平滑处理来估计出参考模型（式（5））。

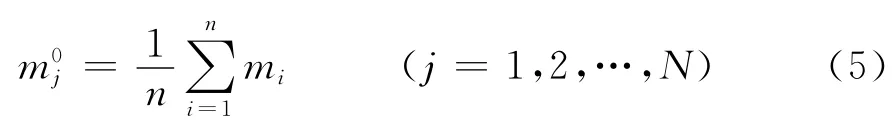
式（5）表示以第j个模型参数mj为中心，取周围n个模型参数做平均（下文称n为平滑的阶数），估计出参考模型的第j个参数，其中N为模型参数的总数。

在反演的开始阶段，n的取值可以较大，超过反演的最大异常体尺度；随着反演迭代的进行，n的取值逐渐减小；在反演的最后阶段，减小到与最小异常体尺度相当或更小。另外，当多种不同类型的模型参数（例如，地层界面和速度）同时反演时，在“反演结果处理”项中就需要分别对不同的模型参数进行多尺度平滑处理。

2 算法验证

为了对提出的反演策略进行验证，作者设计了一个均匀层状模型和两个含异常体的地质模型，进行地震波速度层析成像实验。首先采用球坐标系下波前快速推进（Fast Marching Method，FMM）方法正演计算出理论模型的走时作为观测数据，然后给定与真实模型相差较远的参考模型，最后采用FMM正演算法及子空间反演法进行迭代反演［4］，在迭代过程中通过对参考模型进行修正，使其逐步逼近真实模型。

2.1 均匀层状模型

图2为均匀层状理论模型及观测系统（为了方便，剖面图在直角坐标系下显示），模型范围为地球东经15°～45°E，北纬15°～45°N，深度0km～ 1 000km之间，分为4层，各层具体参数见表1。观测系统的分布范围为地球东经20°～40°E和北纬20°～40°N之间，震源点及接收点的具体分布位置见表2。模型及观测系统的覆盖范围均在2 000 km2以上，可以构建大小不同的地质异常体，从而验证算法对不同规模异常体的分辨率。

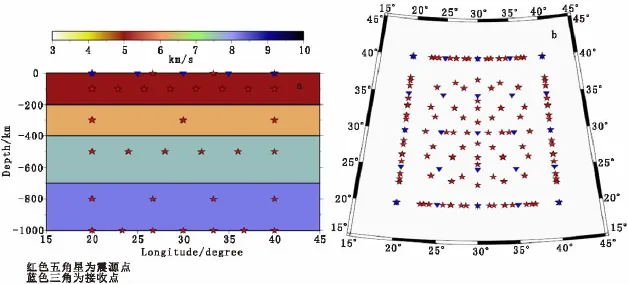
图2 均匀层状理论模型及观测系统Fig.2 Homogeneously stratified model and acquisition geometry

表1 理论模型参数Tab.1 Parameters of theoretical model

反演初始模型如图3所示，四层的速度均为6.75km／s，初始参考模型（这里均将第一次反演迭代中输入的参考模型命名为初始参考模型）与初始模型相同。图4和图5分别是参考模型沿北纬30°和东经30°的剖面，两图分别显示了六次反演迭代过程中参考模型的变化过程。对比分析发现，随着迭代次数的增加，参考模型与真实模型越来越接近，最后一次的参考模型与真实模型相差不远。在反演过程中，为了简化计算，对每次反演迭代后的结果均进行三维五点平滑（5×5×5＝125个点）。

表2 观测系统设计Tab.2 Design of acquisition geometry

图6为改进前算法与改进后算法的反演结果与真实模型的速度差。对比图6中算法改进前后的结果可以看出，在初始参考模型与真实模型相差较远的情况下，其结果均向真实模型靠近，但在模型边界区域两种反演结果的分辨率都较差，其主要原因是由于边界处穿过的射线较少，甚至没有射线穿过。另外，采用未改进算法反演出的结果中含有多个不真实异常体（如A、B、C、D、E等区域），有效区的最大误差约为1.3km／s，最大相对误差26%；改进后算法反演出的结果消除了不真实异常体，有效区的最大误差约为1km／s，最大相对误差20%，而且较大的误差主要集中于模型边界区域。在有效反演区，改进算法反演出的4层平均误差，从上到下分别约为13%、4.84%、2.63%和6.1%，反演的整体速度结构与真实模型基本一致。值得注意的是，中间两层的误差明显小于第一层与第四层，分析其原因是由于给定的初始模型速度与中间两层更加接近，而与其他两层相差较远。虽然该反演方法准确度较依赖于初始模型，但相对于改进前的算法，改进后算法的平均误差大大降低，反演精度得到有效提高。

总的来说，在初始参考模型与真实模型相差较远的情况下，采用作者提出的反演策略及相应的改进算法，参考模型在反演过程中越来越逼近真实模型。相比常规算法，在一定程度上提高了反演结果的精度，这说明了这样的反演策略及相应的改进算法是正确可行的。

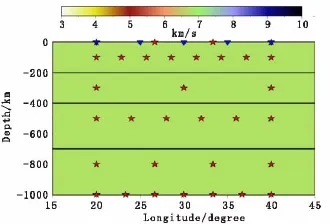
图3 初始模型及初始参考模型Fig.3 Initial model and initial reference model

2.2 含速度异常体模型

前述实验中的模型是比较简单的均匀层状模型，而实际的地球物理模型是十分复杂的。为了验证在有地球物理异常存在的情况下，我们所设计的反演策略与算法也能很好地工作，作者模拟月球质量瘤的地球物理模型，进行进一步的算法实验。

月球质量瘤是当前月球探测中的热点问题之一，其大小、分布及成因有助于研究月球的起源和演化等问题。质量瘤是月球上高密度物质聚集区，可能是由于月球形成早期月幔物质上涌造成的［5－6］，其形状近于圆盘状。根据Konopliv［7］公布的质量瘤分布图，最大的质量瘤直径可达上千公里。相比于其他探测方法，月震层析成像是研究质量瘤形态、规模及分布的最佳手段。但由于月球上仅有四个月震台站的数据可用，台站覆盖密度小，而且相比于地震，月震发生次数非常少，射线覆盖密度低。很多学者利用月震数据对月球进行了大量研究，但至今仍未给出月球内部可靠的结构模型。基于这样的考虑，作者设计了两个大小不同的圆柱形速度异常体模型（本文分别称为大型圆柱体及小型圆柱体）模拟质量瘤，来进行反演实验，验证改进算法对不同规模异常体的分辨能力。

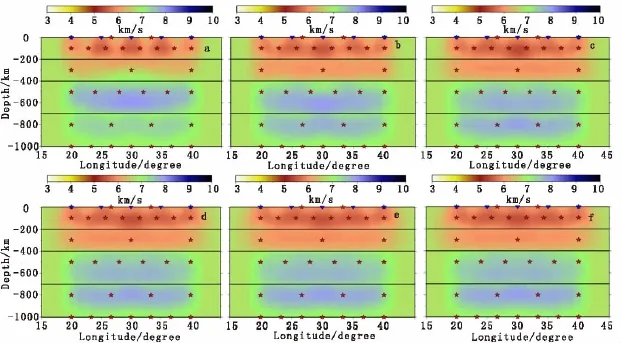
图4 反演迭代过程中参考模型的变化（30°N剖面）Fig.4 Variation of reference model during inversion（cross section along 30°N）

这里使用的观测系统与2.1节中的相同，理论模型除了在第一层中加入了一个大型圆柱形异常体以外，其他参数均与2.1节中的理论模型相同（图7）。大型圆柱异常体的顶底面半径为赤道处5°（经纬度），其中心位置位于30°N／30°E，顶部埋深为50km，底部位于第一层与第二层的界面处，异常体的速度与第二层的速度相同。这样设计的目的是对月球质量瘤进行模拟，模型的第二层作为月幔，圆柱形异常体为一个大型质量瘤，质量瘤与月幔物质速度相同，相当于月幔物质上涌形成的质量瘤。

图5 反演迭代过程中参考模型的变化（30°E剖面）Fig.5 Variation of reference model during inversion（cross section along 30°E）

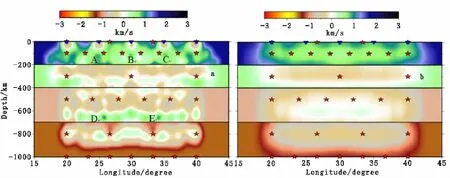
图6 未改进及改进后算法的成像结果在30°N的剖面（用相对速度表示，即成像速度与理论模型速度之差）Fig.6 Cross sections of imaging results along 30°N before and after improved algorithm （difference between imaging result and theoretical model）

反演初始模型及初始参考模型与2.1节中的相同，各层均为6.75km／s，采用改进算法经过6次迭代计算，得到图8和图9所示的结果。由图8和图9可以看出，在含有地质异常体的情况下，每次反演过程中的参考模型逐渐向真实模型靠近，从最后一次输出的参考模型，即本算法的反演结果来看（图8 （f），图9（f）），模型的形态及大小可以比较清晰地分辨出来，并且异常的边界较为清晰，且在有效反演区，改进算法反演出的4层平均误差，从上到下分别约为15.1%、4.98%、2.61%和6.12%，这都说明改进算法对于反演大型异常体，具有较好的反演效果。

图10为小型圆柱异常体模型。小型圆柱形速度异常体的顶、底面半径为赤道处3°，其他各参数均与大型圆柱异常体的相同。采用改进算法经过6次反演迭代的结果如图11所示。由图11可以看出，异常体下部的延伸情况比较清晰，但在切片图上的边界较模糊。

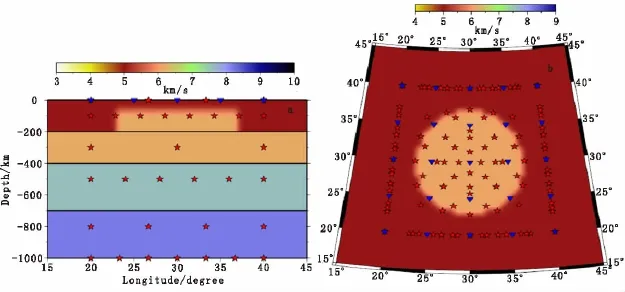
图7 大型圆柱形异常体模型Fig.7 Model with large size of cylindrical anomaly

图8 反演迭代过程中参考模型的变化（100km深度处的切片）Fig.8 Variations of reference model during inversion（slices at depth of 100km）

由两种不同规模异常体的反演结果可以看出，改进后的算法对较大规模的地质构造有较好的适用性；对于小型地质构造，其分辨率明显降低，异常体边界相对模糊，但仍能分辨出来。值得指出的是，在反演过程中，为了简化计算，在模型2和模型3的反演计算中，每次迭代后获取参考模型的处理均为三维五点平滑。

图9 反演迭代过程中参考模型的变化（30°N剖面图）Fig.9 Variations of reference model during inversion（cross section along 30°N）

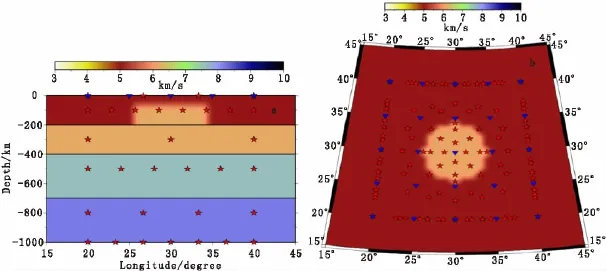
图10 小型圆柱形异常体理论模型Fig.10 Model with small size of cylindrical anomaly

3 结论与讨论

1）在观测数据稀疏、观测系统不能完全覆盖或观测系统布置不合理的情况下，且先验信息也很少的区域，作者提出了通过在反演过程中对参考模型的修正，使参考模型逐步逼近真实模型，从而提高反演精度的新策略。

2）三个理想模型的数值实验，说明了在参考模型远离真实模型的情况下，相比于常规方法，采用这种方法的反演结果与真实模型更加接近，证明了新反演策略及相应的算法是正确可行的。

3）新策略反演算法对那些数据稀疏，且只关心较大型地质构造的反演特别适用。其主要原因在于作者在改进算法中加入了平滑处理以估计新的参考模型，当异常体规模较小时，有可能会被平滑掉。在反演过程中，逐步地减少平滑的阶数是必要的，可使小异常的边界比较清晰。

图11 小型圆柱形异常体反演成像结果Fig.11 Inverted result of the model with small size of cylindrical anomaly

［1］ 姚姚.地球物理反演基本理论与应用方法［M］.北京：中国地质大学出版社，2002.

YAO Y.Basic theory and method of geophysical inversion［M］.Beijing：China University of Geosciences Press，2002.（In Chinese）

［2］ 陈国金.井间地震层析成像中自动生成初始速度模型的方法研究［J］.地球物理学进展，2007，22（6）：1831 －1835.

CHEN G J.Research of automatic generation of initial velocity model in crosswell seismic tomography［J］.Geophysical Prospecting For Petroleum，2007，22（6）：1831－1835.（In Chinese）

［3］ KENNETT B L N，SAMBRIDGE M S，WILLIAMSON PR.Subspace methods for large inverse problem with multiple parameter classes［J］.Geophysical Journal，1988，94：237－247.

［4］ JUPP D L B，VOZOFF K.Stable interative methods for inversion of geophysical data［J］.Geophysical Journal of the Royal Astronomical Society，1975，24：957 －976

［5］ RAWLINSON N.Fast marching tomography package ［EB／OL］.http：／／rses.anu.edu.au／seismology／fmmcode.

［6］ WISE D U，YATES M Y.Mascons as structural relief on a lunar“Moho”［J］.J.Geophys.Res.，1970，75：261－268.

［7］ 金丹.基于层析成像的阿波罗登陆地区月球质量瘤空间分布研究［D］.武汉：中国地质大学，2011.

JIN D.Spatial distribution of lunar mascons in apollo landing area using seismic tomography［D］.Wuhan：China University of Geosciences，2011.（In Chinese）

［8］ KONOPLIV A S，BINDER A B，HOOD L L，et al.Improved gravity field of the moon from lunar prospector.Science［J］.1998，281：1476－1480.

A strategy to improve inversion precision in target area with sparsely distributed observation

Since the observed data of the target area are very sparse，it is difficult to obtain the model which is close to real model only using the observed data.Hence，it is reasonable to add some priori information into inversion and apply the inversion method based on reference model.With the lack of observed data but also and priori information，it is also very difficult to select an appropriate reference model.If an appropriate reference model can＇t be selected，how do we invert for a reliable solution？This paper suggests a strategy to improve inversion precision，which encourages reference model near to real model by stepwise modifying reference model during inversion when the reference model is far away from real model.The authors designed a homogeneously stratified model and two models with the anomaly for testing algorithm.The inversion results illustrate that this strategy is appropriate for inversion of large size of anomaly.

inversion；seismic tomography；sparse observation；model modification method

YANG Ke－si1a，ZHU Pei－min2，ZHAO Na2，XU Yang1b

（1.Jilin Oilfield Branch，PetroChina a.Geophysical Exploration Research Institute，b.Xinmin Oil Production Factory，Songyuan 138000，China；2.China University of Geosciences，Institute of Geophysics and Geomatics，Wuhan 430074，China）

P 631.4

：A

10.3969／j.issn.1001－1749.2015.06.11

1001－1749（2015）06－0735－08

2014－11－28改回日期：2015－03－22

杨克思（1990－），男，硕士，主要研究方向为地震资料解释与反演，E－mail：yangkesi＠foxmail.com。