交错网格高阶差分算法的改进

白亚东，冯志民，杨庆节

（1.中国地质大学 地球物理与信息技术学院，北京 100083；2.宁夏地球物理地球化学勘查院，银川 750004；3.吉林大学 地球探测科学与技术学院，长春 130026）

交错网格高阶差分算法的改进

白亚东1，2，冯志民2，杨庆节3

（1.中国地质大学 地球物理与信息技术学院，北京 100083；2.宁夏地球物理地球化学勘查院，银川 750004；3.吉林大学 地球探测科学与技术学院，长春 130026）

利用Taylor公式展开导出了交错网格中可导函数任意次导数的任意偶数阶精度的差分近似式及相应的差分系数，从而改进了常规高精度交错网格有限差分算法中对各个空间导数采用不一致精度的问题。采用推导的交错网格高阶差分算法对一阶弹性波动方程进行数值模拟，得到了精确的数值模拟结果，证明了推导的交错网格高阶差分算法的正确性。

交错网格；有限差分；数值模拟

0 引言

数值模拟问题出现在多个学科分支中，地震波场的数值模拟就是理解地震波在复杂介质中传播的不可或缺的工具。有限差分和伪谱法是两种使用较为广泛的地震波场数值模拟方法，虽然理论上讲伪谱法是高阶有限差分法中空间差分的阶数达到无穷时的极限情况［1］，但是有限差分由于自身的易实现性，仍然得到了许多科研人员的重视。

有限差分算法不仅应用于地震波场模拟上，地震波的偏移成像和反演等也多有应用。为了提高有限差分算法的计算精度、稳定性和适用性，该方法出现了多种变种方法：变网格有限差分［2－3］、不连续网格有限差分［4］、不规则网格有限差分［5］、交错网格有限差分［6－7］、旋转交错网格有限差分［8－9］、可变时间步长有限差分［10］、自适应可变空间步长网格有限差分以及隐式有限差分［11－12］。

交错网格是由 Madariage［13］最早提出，Virieux［6］首先将其使用到一阶速度－应力方程中。Virieux发展的交错网格的精度为O（Δt2＋Δx2），与常规网格相比既没有增加计算量又没有增加存储空间，局部精度却提高了4倍，收敛速度也有所提高。Levander［14］又将交错网格有限差分的精度提高到O（Δt2＋Δx4）。由于交错网格有限差分与传统有限差分比较，具有更高的精度和更好的稳定性，常被应用于近地表复杂地形的模拟，粘弹性波场模拟［15－16］也已经使用了交错网格有限差分算法。

董良国等［17］发展了更高精度的交错网格有限方法，精度达到了O（Δt4＋Δx2 N），为了使用较少的时间层，不增加计算存储空间，将速度（应力）对时间的三次导数准确地转化为应力（速度）对空间的导数，把交错网格和高阶差分法成功地结合在一起，这种高阶交错网格有限差分解法，能够适用于求解二维或者三维任意介质情况下由速度－应力表示的弹性波方程；李振春等［18］提出一种新的基于高阶交错网格技术，通过改变网格空间步长实现局部网格加密，弥补了常规网格中因采样不足导致的频散现象；李萌［19］在董良国的工作基础上改进了差分格式中三次导数的差分近似方法；刘洋等［20］通过引入Claerbout［21］的高阶分母相，推导出一种新的隐式交错网格有限差分公式，该公式对一阶空间导数的（2 N＋2）阶精度的差分，相当于常规交错网格有限差分公式的4 N阶精度的差分，且在提高精度的同时，并不增加计算成本；刘洋等［11］还将Claerbout的思想与正规网格有限差分方法相结合，同样得到了很好的效果。

作者着眼于常规交错网格算法中对空间任意导数的高阶差分，以Taylor公式展开为基础，推导出了可导函数任意次导数的任意偶数阶精度的差分近似式以及差分系数，从而改进了O（Δt4＋Δx2 N）一阶速度－应力方程组差分格式和差分系数.这里推导的差分格式与常规的高阶交错网格差分格式相似，但当变量对空间求三次导数时，给出了更精确的差分系数，而差分系数的精确度正是决定交错网格有限差分算法精度的关键。比较本方法和常规方法在相同条件和相同精度下的正演波形，结果显示本方法的波形与解析解的误差更小，稳定性更好。

1 改进的交错网格差分格式

在二维TI介质中，假定外力为零，一阶速度－应力弹性波方程为：

其中：vx、vz为分别为速度在x、z方向上的分量；τxx、τzz、τxz为应力分量；ρ为密度；cij为介质的弹性常数。式中的速度和应力呈现一种耦合递推的关系，适用于交错网格差分算法。

1.1 时间上的差分近似

式中：Δt为时间步长，令M＝2，式（6）就是常规的时间4阶精度差分近似。为了减少计算内存，利用速度和应力的耦合关系，得到式（1）―式（5）的时间4阶精度差分近似，以式（1）为例：

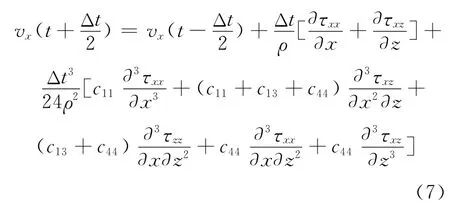
1.2 空间上的差分近似

为了改进精度为“O（Δt4＋Δx2 N）”的常规差分格式，这里对式（7）中各变量对空间二次、三次导数的差分格式进行改进，求解函数任意次（奇数次和偶数次）导数的任意偶数阶精度的差分系数。

首先推导离散化函数值在半网格点上时，差分近似式的差分系数如图1所示，f（x）的n次导数的差分使用的离散化函数值在半网格点上。

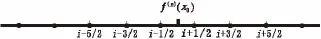
图1 交错的网格点Fig.1 Form of staggered points

式（8）写成矩阵的形式有：

其中

简单记为：X＝B·D，所以F＝D－1·B－1·S，若设F＝C·S，则有

式中C就是差分系数矩阵。由于D是初等矩阵，所以

则式（10）可写为式（11）。

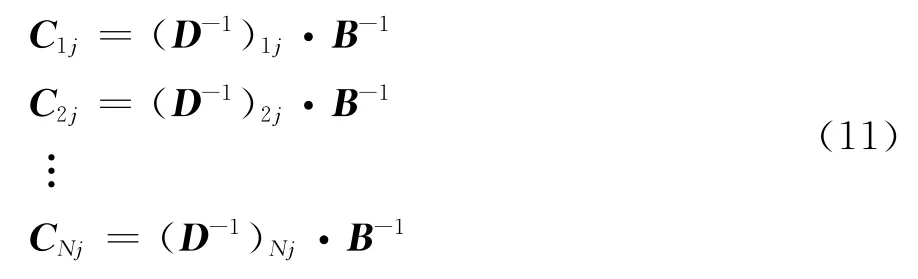
方便起见，这时只观察式（11）中第一个式子，两边取转置有，

因此有

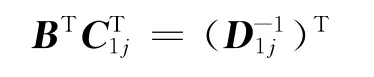
即

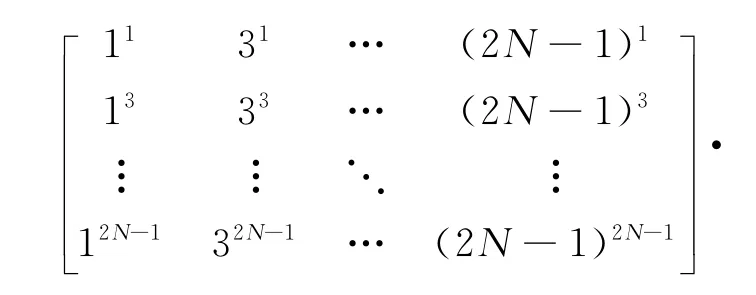
通过求解式（12）可以得到一次导数差分格式的2 N阶精度的差分系数，同理式（11）中其他的N－1个式子都可以得到类似式（12）的方程，即

式中C（N－i＋1）in表示函数f（x）的2i－1次导数的2（N －i＋1）阶精度的差分系数（i，n＝1，2，…，N）。该式包含常规求一次导数差分近似式系数的矩阵方程，由于N不能小于i，所以此时的差分精度为2（N －i＋1）阶，i＝1时也成立。因此有差分近似式：

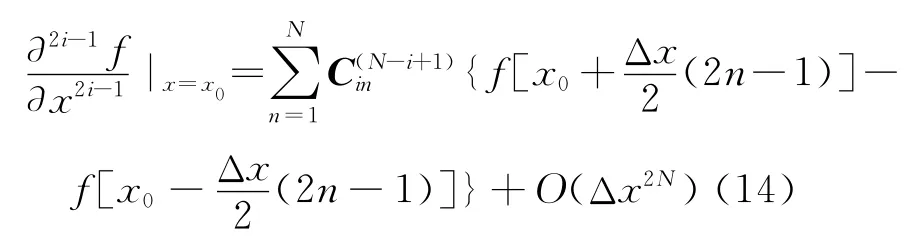
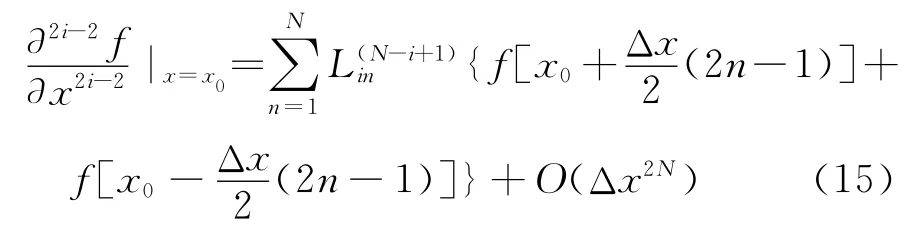
然后推导离散化函数值在整网格点上时，差分近似式的差分系数如图2所示，f（x）的n次导数的差分使用的离散化函数值在整网格点上.

令函数f（x）在x＝x0±nΔx处进行Taylor展开，接下来的推导过程相同，不在详述细节。

式（17）、式（18）分别是图2所示情况下函数f（x）的任意奇数次和任意偶数次导数的差分近似式，其差分精度与交错网格上的一致。同时给出了差分系数的求解矩阵方程。

1.3 改进后的差分格式

在确定了差分系数之后，将对应的变量对空间一次、二次和三次导数差分近似式代入到一阶速度－应力方程式（1）―式（5）中，经过整理，得到其精度为O（Δt4＋Δx2 N）的改进后准确的差分格式，以式（1）为例：

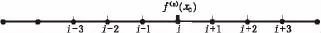
图2 非交错的网格点Fig.2 Form of non－staggered points

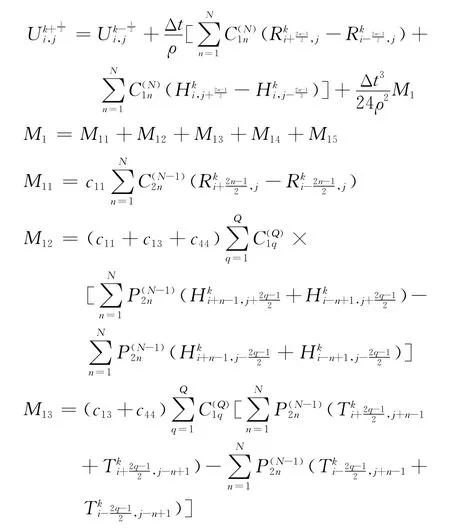
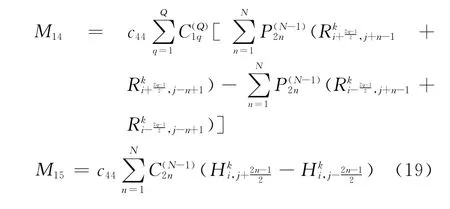
表1 常用差分精度的稳定性条件Tab.1 Sbility conditions of common difference accuracy

2 稳定性条件

通过傅里叶分析方法，在二维TI介质XOZ面内，空间网格间距、时间采样间隔和波速要满足式（20）。

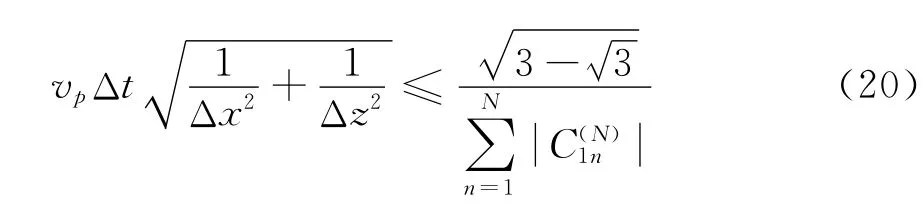
由式（20）计算得到几种常用差分精度的稳定性条件，如表1所示，其中。

3 精度对比以及模型试算

3.1 精度对比

为了验证改进后的交错网格有限差分法的精度和正确性，将改进前后的正演结果进行比较。

各向同性均匀介质如图3所示，物性参数纵波速度为3 000m／s，横波速度为2 000m／s，介质密度为2 000kg／m3。震源坐标为（1 000m，1 000 m），采用主频为25Hz的Richer子波激发。时间采样间隔为0.001s，模型网格大小为200m×200 m，水平和垂直空间步长都为10m，模型自由表面采用PML吸收边界。

图3 各向同性均匀介质模型Fig.3 Isotropic medium model

图4 250ms时模型波场快照Fig.4 Snapshots of Fig3at 250ms

分别使用不同精度的常规交错网格有限差分公式和本文推导的交错网格有限差分公式对一阶速度－应力波动方程（方程（1）－方程（5））进行模拟，模拟结果图4中展示。

图4分别是精度为O（Δt4＋Δx4）和O（Δt4＋Δx10）常规交错网格有限差分算法改进前后的250 ms时的波场快照，可以看出，改进前、后的高精度交错网格有限差分算法在相同精度下，改进后的模拟结果的精度有较大的提高，波场频散情况明显改善。为了更加清晰地对比改进前后的精度，将其精度为O（Δt4＋Δx10）正演波形同时与解析解波形进行比较。图5给出的是模型中坐标为（500m，500m）质点处的振动记录数值解与解析解的比较，由图5可见，改进后的数值解波形与解析解更加一致，说明改进后的高阶交错网格有限差分算法精度更高。

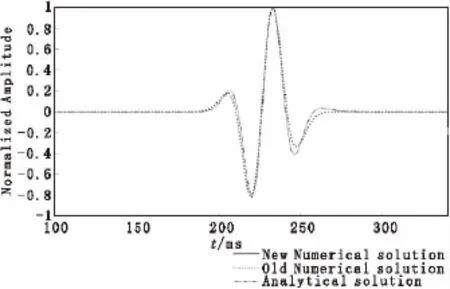
图5 算法改进前后的质点振动记录与解析解的对比Fig.5 Comparison of particle vibration recorded before and after the improved algorithm and analytic solutions

3.2 双层模型试算

为了研究波场在层状介质中的传播规律，建立层状地质模型，图6是分层均匀介质模型，每层的物性参数如图6所示。网格大小为250m×250m，空间步长为10m，两个介质分界面分别在500m深和1 000m深处。震源坐标为（200m，1 250m），计算时采用改进后的时间4阶空间10阶精度的差分格式，用主频为25Hz的Richer子波激发。模型四周均采用PML吸收边界。

图6 分层介质模型Fig.6 Layered medium model

图7分别是精度为O（Δt4＋Δx8）的改进后算法的400ms时的波场快照，可以看出，完善后的高精度交错网格有限差分算法，能精确地模拟弹性波在地下层状介质中的传播特性，各种反射和透射波都可以观察到。在自由表面也没有看到明显的反射，说明将PML吸收边界应用到改进后的交错网格算法中，对弹性波也有很好的吸收效果。

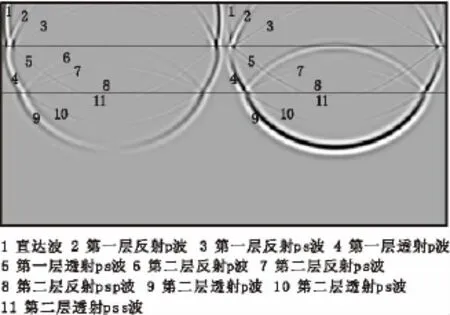
图7 400ms时模型波场快照Fig.7 Snapshots of Fig6at 400ms

4 结论

交错网格有限差分以其高效、精确、实用等优点常被用于波动方程模拟。作者通过Taylor公式展开法推导了函数任意次导数的任意阶精度的差分格式及其差分系数，改进了传统的高精度交错网格有限差分公式。通过精度对比及模型试算的结果表明，在计算量增加不大情况下，改进后的高精度交错网格有限差分公式比常规传统的公式精度更高。

［1］ 唐小平，白超英，刘宽厚.伪谱法分离波动方程弹性波模拟［J］.石油地球物理勘探，2012，47（1）：19－26.

TANG X P，BAI CH Y，LIU K H.Elastic wavefield simulation using separated equations through pseudospectral method［J］.OGP，2012，47（1）：19－26.（In Chinese）

［2］ WANG Y，XU J，GERARD T S.Viscoelastic wave simulation in basins by a variable－grid finite－difference method［J］.Bull Seismol Soc Am，2001，91（6）：1741 －1749.

［3］ NARAYANJ P，KUMAR S.A fourth order accurate SH－wave staggered grid finite－difference algorithm with variable grid size and VGR－stress imaging technique［J］.Pure applGeophys，2008，165：271－294.

［4］ SHIN A，HIROYUKI F.3Dfinite－difference method using discontinuous grids［J］.Bull SeismolSoc Am，1999，89：918－930.

［5］ OPRŠAL I，ZAHRADNíK J.Elastic finite－difference method for irregular grids［J］.Geophysics，1999，64：240－250.

［6］ VIRIEUX J.SH－wave propagation in heterogeneous media：velocity－stress finite－difference method：Geophysics［J］.1984，49（11），1933－1957.

［7］ THOMAS B，ERIK H S.Accuracy of heterogeneous staggered－grid finite－difference modeling of rayleigh waves［J］.Geophysics，2006，71（4）：T109－T115.

［8］ ERIK H S，NORBERT G，SERGE A S.Modeling the propagation of elastic waves using a modified finitedifference grid［J］.Wave Motion，2000，31：77－92.

［9］ REESHIDEV B，MRINAL K S.Finite－difference modelling of S－wave splitting in anisotropic media［J］.Geophysical Prospecting，2008，56：293－312.

［10］TESSMER E.Seismic finite－difference modeling with spatially varying time steps［J］.Geophysics，2000，65 （4）：1290－1293.

［11］LIU Y，MRINAL K S.A practical implicit finitedifference method：examples from seismic modeling ［J］.Journal of Geophysics and Engineering，2009（6）：231－249.

［12］LIU Y，MRINAL K S.Finite－difference modeling with adaptive variable－length spatial operators［J］.Geophysics，2011，76（4）：T79－T89.

［13］MADARIAGA R.Dynamics of an expanding circular fault［J］.Bull Seismol Soc Am，1976，66，639－666.

［14］LEVANDER A R.Fourth－order finite－difference PSV seismograms［J］.Geophysics，1988，53（11）：1425 －1436.

［15］OPERTO S，VIRIEUX J，AMESTOY P，et al.3Dfinite－difference frequency－domain modeling of visco－acoustic wave propagation using a massively parallel direct solver：Afeasibility study［J］.Geophysics，2007，72：SM195－SM211.

［16］LIAO J P，WANG H Z，AND MA Z T.2－D elastic wave modeling with frequency－space 25－point finitedifference operators［J］.Applied Geophysics，2009，6 （3）：259－266.

［17］董良国，马在田，曹景中.一阶弹性波方程交错网格高阶差分解法稳定性研究［J］.地球物理学报，2000，43 （3）：411－419.

DONG L G，MA Z T，CAO J ZH.The Staggered－Grid High－Order Difference Method of One－Order E－lastic Equation［J］.Chinese Journalof Geophysics，2000，43（3）：411－419.（In Chinese）

［18］李振春，张慧，张华.一阶弹性波方程的变网格高阶有限差分数值模拟［J］.石油地球物理勘探，2008，43（6）：711－716.

LI ZH CH，ZHANG H，ZHANG H.Variable－grid high－order finite－difference numeric simulation of first －order elastic wave equation［J］.OGP，2008，43（6）：711－716.（In Chinese）

［19］李萌.改进的一阶弹性波方程交错网格高阶差分解法［J］.地球物理学进展，2009，24（3）：1065－1068.

LI M.Improvement to the staggered－grid high－order difference method of one－order elastic wave equation ［J］.Progress in Geophys，2009，24（3）：1065－1068.（In Chinese）

［20］LIU Y，MRINAL K S.An implicit staggered－grid finite－difference method for seismic modeling［J］.Geophysical Journal International，2009，179：459－474.

［21］CLAERBOUT J F.The craft of wavefield extrapolation，in Imaging theEarth's Interior［M］.Oxford：Blackwell Scientific Publications，1985.

Improvement of staggered grid finite difference algorithm

BAI Ya－dong1，2，FENG Zhi－min2，YANG Qing－jie3
（1.School of Geophysics and Information Technology，China University of Geosciences，Beijing 100083，China；2.Ningxia Academy of Geophysical and Geochemical Exploration，Ningxia 750004，China；3.College of GeoExploration Science and Technology，Jilin University，Changchun 130026，China）

A finite difference scheme with any－order accuracy and corresponding coefficients of any number of derivatives of functions which have any number of derivatives by Taylor formula is deduced in this paper.It is helpful to improve the staggered grid finite difference algorithm which has inconsistent accuracy in difference space derivatives.We make a simulation of seismic response with conventional FD scheme and the new FD scheme respectively.As a result，the new FD scheme is more stabilized and more accurate.

staggered grid；finite difference；numerical simulation

P 631.4

：A

10.3969／j.issn.1001－1749.2015.06.07

1001－1749（2015）06－0709－07

2014－11－26改回日期：2015－03－24

宁夏回族自治区地勘基金项目（2014－地勘基金07）

白亚东（1975－），男，高级工程师，长期从事地球物理勘探工作，E－mail：byd1975＠163.com。