基于稀疏组LASSO约束的本征音子说话人自适应

屈丹，张文林

（信息工程大学 信息系统工程学院，河南 郑州 450000）

1 引言

连续语音识别系统中训练数据与测试数据的不匹配会造成系统性能的急剧下降。声学模型自适应技术就是根据少量的测试数据对声学模型进行调整，增加其与测试数据的匹配程度，从而提高系统的识别性能。造成训练与测试数据不匹配的因素包括说话人、传输信道或说话噪声环境等，相应的自适应技术分别称为“说话人自适应[1]”、“信道自适应[2]”或“环境自适应[3]”。说话人自适应技术的方法也可以应用于信道自适应或环境自适应。说话人自适应通常包括特征层自适应[4,5]和声学模型自适应，因此，声学模型的说话人自适应[1]是当前语音识别系统一个必不可少的重要组成部分。

声学模型的说话人自适应就是利用少量的未知说话人语料(自适应语料)，在最大似然或最大后验准则下，将说话人无关(SI, speaker independent)声学模型调整至说话人相关(SD, speaker- dependent)声学模型，使语音识别系统更具说话人针对性，从而提高系统的识别率。在隐马尔可夫模型的连续语音识别系统框架下，主流的说话人自适应技术可分为3大类[1]：基于最大后验概率、基于变换和基于说话人子空间的自适应方法，分别以最大后验（MAP, maximum a posteriori）自适应、最大似然线性回归（MLLR, maximum likelihood linear regression）及本征音(EV, eigenvoice)方法及其相应的拓展算法为代表。2004年，Kenny等[6]通过对SD声学模型中各高斯混元均值矢量相对于 SI声学模型的变化量进行子空间分析，得到一种新的子空间分析方法。该方法与说话人子空间中的“本征音”类似，因此称该子空间的基矢量为“本征音子（EP, eigenphone）”，该空间为“音子变化子空间”，但该方法采用“多说话人”声学建模技术，只能得到训练集中说话人相关的声学模型，对于测试集中的未知说话人没有给出其声学模型的自适应方法。2011年，文献[7]提出了一种基于本征音子的说话人自适应方法，克服了 Kenny等方法的不足，能够对测试集未知说话人进行自适应。但该方法在自适应阶段需要估计一个高维的扩展本征音子矩阵，故其待估参数数量多于传统说话人自适应方法，因此在自适应数据量充足时，可以得到更好的自适应性能。然而，当自适应数据量不足时，即使采用说话人自适应训练（SAT, speaker adaptation training）等技术，仍会出现严重的过拟合现象。

正则化方法是目前很多领域的一种非常有效的提高模型参数稳健性的方法，在连续语音识别系统说话人自适应中也逐步应用。例如，文献[8]将l2正则化方法应用于 MLLR自适应方法的变换矩阵估计，得到一种正则化的 MLLR说话人自适应方法，并在单句话的无监督说话人自适应中取得了良好的效果；文献[9,10]提出稀疏最大后验（SMAP,sparse maximum a posteriori）自适应方法，该方法可以在减少模型存储量的同时提高MAP自适应的效果，随后文献[11]又采用λ1正则化进行改进。文献[12]将λ1正则化、l2正则化和弹性网正则化方法应用于本征音说话人自适应，识别率得到进一步提升。

为此，本文提出了基于稀疏组LASSO约束的本征音子说话人自适应方法。新方法本质上是以本征音子作为字典项；在模型域寻求说话人相关模型参数的稳健性稀疏表达；对自适应问题的目标函数引入稀疏组 LASSO正则项, 在自适应阶段通过优化过程自动选择说话人相关音子子空间基矢量及其组合系数。文中给出了一般正则化本征音自适应原理框架，并讨论了组稀疏正则化方法和稀疏组 LASSO正则化，分别给出了其数学优化算法。

2 本征音子说话人自适应

2.1 音子变化子空间及本征音子

2.2 本征音子的最大似然估计算法

3 基于稀疏组LASSO约束的本征音子说话人自适应

本征音子说话人自适应方法在自适应阶段需要估计一个D×(N+ 1 )维的扩展本征音子矩阵，其待估参数数量多于传统说话人自适应方法，因此在自适应数据量充足时，可以得到更好的自适应性能。然而，当自适应数据量不足时，即使采用说话人自适应训练等技术，仍会出现严重的过拟合现象。文献[14]分别通过引入先验分布和对本征音子矩阵引入低秩约束来解决这一问题，但提升的性能有限，因此可以考虑更好的约束方法来解决这一问题。

扩展本征音子矩阵的最大似然估计问题，引入正则化方法后，说话人自适应目标函数变为

3.1 组稀疏正则化方法

3.2 稀疏组LASSO正则化方法

组稀疏正则化方法使估计结果中的非零组尽量少，然而却无法保证组内参数的稀疏性。对于扩展的本征音子矩阵估计问题，组稀疏正则化可以使估计得到的矩阵V% 的某些列同时为0，然而不为0的那些列却往往不是稀疏的。事实上λ1正则化可以控制矩阵V% 列内参数的稀疏性，因此可以将λ1正则化与组稀疏正则化相结合，得到更为稳健的估计，称为“稀疏组LASSO（SGL, sparse-group LASSO）”正则化方法[17]，其正则化函数

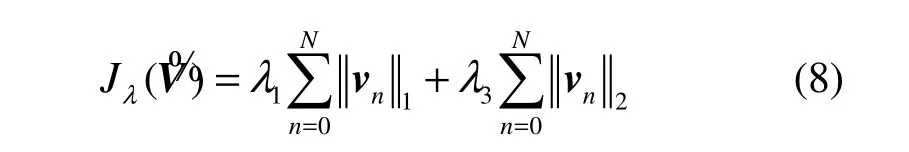
这意味着首先通过组稀疏正则化方法选择不为零的那些参数组，然后通过λ1正则化方法选择组内的非零参数。对于扩展的本征音子矩阵估计问题，相当于对待估矩阵同时施加列间和列内稀疏性约束，从而得到结构化的稀疏解。

式(8)与弹性网正则化函数很相似，然而这里的l2范数没有平方运算，可以证明在每一个不为0的组（本征音子vn）内，稀疏组LASSO正则化方法相当于一种特殊的弹性网正则化方法[17]。

3.3 稀疏组LASSO约束的本征音子自适应优化算法

对于组稀疏正则化与稀疏组LASSO正则化问题，常用的解法有快速迭代收缩域值算法(FISTA,fast iterative shrinkage-thresholding algorithm)[19]、加速的广义梯度下降算法[17]等，文献[20]也给出了多种正则化函数适用的一种通用数学优化方法——递增近点梯度(IPG, incremental proximal gradient)算法。由于本文的优化问题包含一个可导的正则项（l2正则项）和多个不可导的正则项（λ1正则项和组稀疏正则项），对于这种问题，递增近点梯度法是一种通用的、行之有效的迭代算法；而FISTA算法中的动量法及其选择的参数（(k)t的更新公式）可以对迭代过程进行加速。为此本文在递增近点梯度算法中引入动量法（momentum method）[19]加速其收敛过程，得到一种“加速递增近点梯度（AIPG, accelerated incremental proximal gradient）算法”。

在算法1中，第②步采用动量法[14]来加快其迭代收敛过程；第③步为原始递增近点梯度算法的迭代公式，其中，别为λ1正则函数、l2正则函数和组稀疏正则函数的近点映射算子[21]，η(k)是第k步迭代的步长；为进一步加快收敛速度，本文对η(k)进行线性搜索，即在第④步当检测到迭代后的目标函数值变大时，按0.8的加权系数减小步长η(k)，重新回到第③步；最后，检查本次迭代前后Q%的相对减少量是否小于门限 10-5，若是则停止迭代，否则回到步骤②重新进行迭代。

4 实验结果及分析

为了验证本文算法的性能，采用微软中文语料库[18]进行连续语音识别的说话人自适应实验。训练集包括100个男性说话人，每人约200句话，共有19 688句话，每句话时长大约5 s，总时长为33 h。测试集中共有25个说话人，每人20句话，每句话时长也约为5 s。

声学特征矢量采用13维的MFCC参数及其一阶、二阶差分，总特征维数为 39维。帧长和帧移分别为25 ms和10 ms。实验中，借助语音开源工具箱HTK（hidden Markov toolkit）（版本3.4.1）[13]训练得到SI基线系统。首先训练单音子声学模型，其中每个单音子对应一个汉语有调音节。根据发音字典，对单音子进行上下文扩展，得到295 180个跨词的三音子有调音节，其中95 534个三音子在训练语料中得到覆盖。每个三音子用一个包含3个发射状态的、自左向右无跨越的隐马尔可夫模型进行建模。采用基于决策树的三音子状态聚类后，系统中共有2 392个不同的上下文相关状态。最终训练得到的说话人无关（SI）声学模型中每个状态含有8个高斯混元，因此声学模型中的总高斯混元数为19 136个。

在测试阶段，采用音节全连接的解码网络，不采用任何语法模型。采用这种解码网络的语音识别系统对声学模型的要求最高，可以充分展示声学模型的识别性能。在原始测试集上，SI基线系统的平均有调音节正确识别率为53.04%（文献[18]中结果为51.21%)。

为了便于比较本文算法的性能，本文针对下列说话人自适应算法进行对比实验。

1) EPNew：采用最大似然估计的本征音子自适应，且进行说话人自适应训练得到的方法，简称EPNew方法。首先采用主分量分析得到本征音子矩阵和高斯混合坐标矢量；其次利用训练数据重新SAT后的模型；然后采用最大似然准则估计本征音子矩阵，采用λ1约束的最大似然准则估计高斯混合坐标矢量；不断迭代得到最终的SAT模型和各高斯混合坐标矢量。由于该算法具有较好的性能，因此作为后续算法的基线系统。

2) EPNew-L1：基于λ1约束的EPNew自适应算法，λ1范数权重λ1从10 调整到40。

3) EPNew- L2：基于l2约束的EPNew自适应算法，l2范数权重λ2从10调整到2 000。

4) EPNew-L1-L2：基于弹性网正则化约束的EPNew自适应算法，其中λ1从10到20，λ2从10调整到100。

5) EPNew-GS：基于组稀疏正则化约束的EPNew自适应算法，组稀疏权重λ3从60调整到150。

6) EPNew- SGL:基于稀疏组 LASSO 约束的EPNew自适应算法，其中λ1从10到20，λ2从10调整到40。

为了比较各种方法在不同自适应数据量下的自适应效果，对每个测试说话人分别随机抽取 1句、2 句、4 句、6 句、8 句和 10 句话作为自适应数据，从剩下语句中随机抽取 10句话作为测试数据，重复该过程8次，得到8组实验数据，将8组数据的平均结果作为系统性能指标。表 1、表 2中黑体字所示为每种自适应数据量条件下的最好实验结果，斜体字所示为引入正则化约束后平均正确识别率下降的实验结果。

4.1 经典正则化约束的本征音子自适应实验

适当引入约束条件可以提升系统性能，为了便于比较本文算法的性能，以EPNew为基线系统，首先将λ1正则化、l2正则化和弹性网正则化3种经典正则化方法引入到基线系统中来。

表1给出了本征音子算法EPNew在3种经典正则化方法下的实验结果，括号内数字表示所有测试说话人扩展本征音子矩阵稀疏度的平均值

表1结果表明，引入λ1正则化方法之后，自适应性能得到提高，特别是在自适应数据量不足时（少于4句话时），性能的提升尤为明显，过拟合现象得到有效缓解。对于某一个固定的正则化因子λ1（对应表1中EPnew-L1方法中的某一行），随着自适应数据量的增加，平均稀疏度逐渐减小，表明扩展本征音子矩阵中的非零元素数量逐渐增加，更多的自适应参数得到估计，因此λ1正则化方法具有良好的参数选择功能，它可以使自适应参数数量随着数据量的增加而不断增多。

在各种自适应数据量下，随着正则化因子λ1的增大（对应 EPnew-L1算法中的某一列），扩展本征音子矩阵的平均稀疏度也不断增大，而平均正确识别率先增后减。当自适应数据量为 1、2、4、6句话时，自适应方法在λ1=20时取得最好的效果，而当自适应数据量更为充足时（8句话和10句话时），λ1= 1 0可以取得更好的结果。

引入l2正则化后，当自适应数据量很少时（1或2句话时），系统的性能有了明显提高，且λ2越大性能提高越明显；而当自适应数据量较为充足时（多于4句话时），随着λ2的增大，平均正识率先增后减，且λ2越大，系统性能的下降越明显（如表1中斜体字所示部分）。因此随着自适应数据量的增加，应逐渐减小λ2的值以放松约束，从而获得更好的自适应效果。

从表1中方法的对比结果来看，总体来讲，l2正则化的效果不如λ1正则化。相关研究表明两者具有一定的互补性，因此本文也对弹性网正则化方法进行测试，它是λ1和l22种正则化方法的一种线性组合。实验中，将λ1正则化因子λ1分别固定为10或20，将l2正则化因子λ2从10调整至100。在引入l2正则化方法后，与原始的λ1正则化方法相比（λ1＞ 0 ,λ2= 0 时），弹性网正则化方法的平均正识率略有所提升。且随着自适应数据量的增加，l2正则化因子λ2应逐渐减小；当l2正则化因子取得过大时，平均正识率反而会下降。

表1 经典正则化自适应算法的实验结果（正识率）（%）（括号内数字表示平均稀疏度）

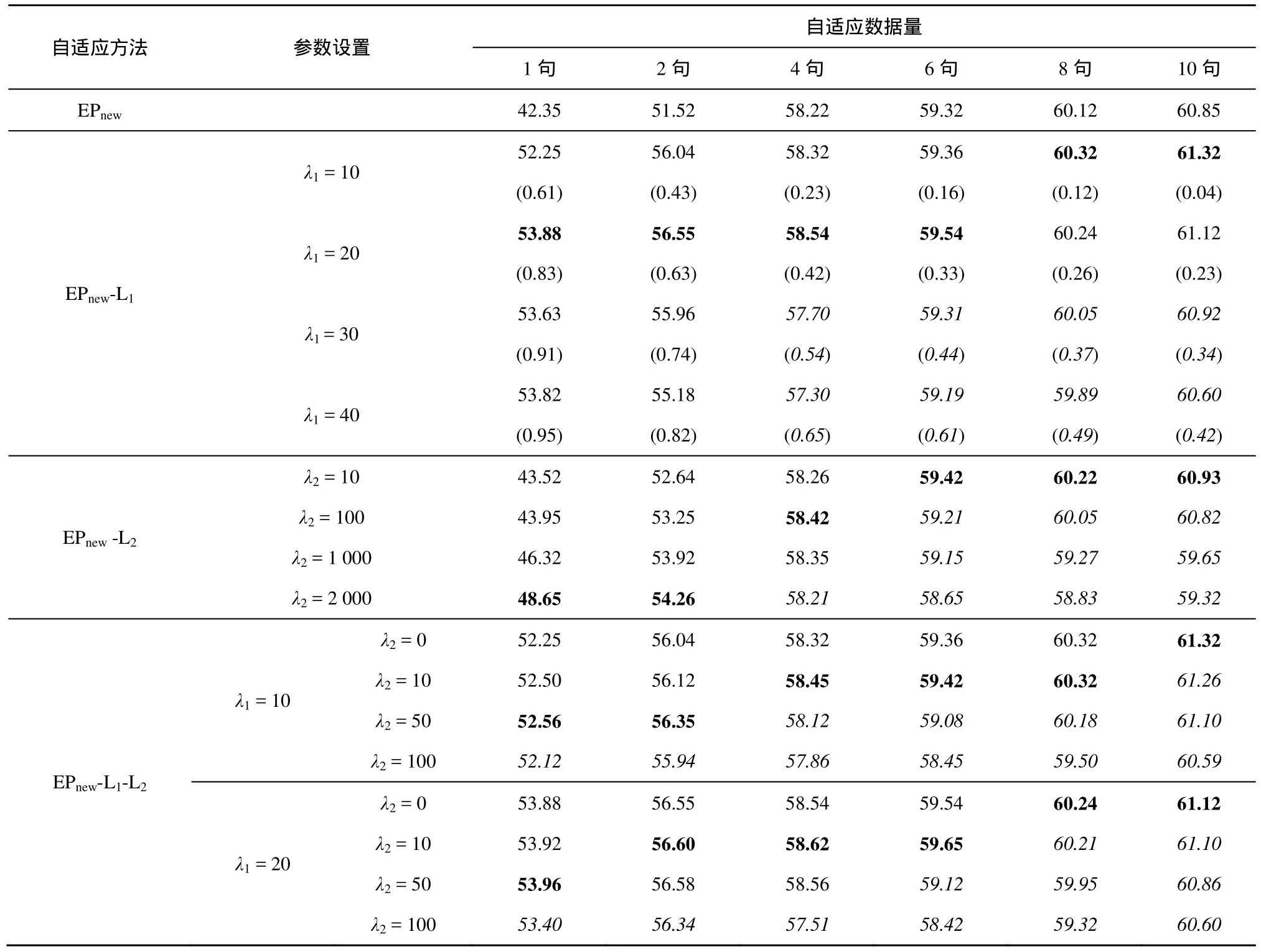
表1 经典正则化自适应算法的实验结果（正识率）（%）（括号内数字表示平均稀疏度）

自适应方法 参数设置自适应数据量1句 2句 4句 6句 8句 10句EPnew 42.35 51.52 58.22 59.32 60.12 60.85 λ1 = 10 52.25(0.61)56.04(0.43)58.32(0.23)59.36(0.16)60.32(0.12)61.32(0.04)EPnew-L1 λ1 = 20 λ1 = 30 53.88(0.83)53.63(0.91)56.55(0.63)55.96(0.74)58.54(0.42)57.70(0.54)59.54(0.33)59.31(0.44)60.24(0.26)60.05(0.37)61.12(0.23)60.92(0.34)λ1 = 40 53.82(0.95)55.18(0.82)57.30(0.65)59.19(0.61)59.89(0.49)60.60(0.42)λ2 = 10 43.52 52.64 58.26 59.42 60.22 60.93 EPnew -L2 λ2 = 100 43.95 53.25 58.42 59.21 60.05 60.82 λ2 = 1 000 46.32 53.92 58.35 59.15 59.27 59.65 λ2 = 2 000 48.65 54.26 58.21 58.65 58.83 59.32 λ2 = 0 52.25 56.04 58.32 59.36 60.32 61.32 EPnew-L1-L2 λ1 = 10 λ2 = 10 52.50 56.12 58.45 59.42 60.32 61.26 λ2 = 50 52.56 56.35 58.12 59.08 60.18 61.10 λ2 = 100 52.12 55.94 57.86 58.45 59.50 60.59 λ2 = 0 53.88 56.55 58.54 59.54 60.24 61.12 λ1 = 20 λ2 = 10 53.92 56.60 58.62 59.65 60.21 61.10 λ2 = 50 53.96 56.58 58.56 59.12 59.95 60.86 λ2 = 100 53.40 56.34 57.51 58.42 59.32 60.60

4.2 稀疏组LASSO约束的本征音子自适应实验

本节针对组稀疏正则化和稀疏组LASSO正则化方法进行自适应实验。由上面分析可知，利用式(6)给出的组稀疏正则化函数，使估计得到的扩展本征音子矩阵V%出现许多元素全为0的列。为了了解正则化因子λ3对矩阵V% 的列稀疏性影响，定义“列稀疏度”θ为矩阵V%中全为0的列数占总列数的比例。实验中将组稀疏正则化因子λ3从60调整到150。更重要一点，本节将通过实验验证组稀疏正则化与λ1正则化的互补性，将两者进行线性组合，得到稀疏组 LASSO正则化方法。实验中，将λ1正则化因子λ1分别固定为10和20，改变组稀疏正则化因子λ3的值进行实验。

表2给出了不同自适应数据量下的典型实验结果，表中括号内单个数字为所有测试说话人扩展本征音子矩阵的平均列稀疏度，以2个数字()的形式分别表示扩展本征音子矩阵的“平均稀疏度与“平均列稀疏度。

由表2可见，在自适应数据量较少时，引入组稀疏正则化后，系统识别性能得到显著提高；随自适应数据量的增大，应逐渐减少正则化因子λ3以获得更好的自适应效果。在相同的自适应数据量下（列纵向比较），随着λ3的增大，平均列稀疏度也逐渐增大，而平均正识率却先增后减。正则化因子对平均列稀疏度的影响在自适应数据量少时（如1句话时）更为明显，而当自适应数据量超过4句话时，平均列稀疏度始终接近于 0，这是由于正则化函数的近点映射算子[21]本质上是一个乘性收缩算子，因此迭代若干次后，会使矩阵某些列的元素值变小，却难以完全等于0。对比表 2和表 1结果可见，组稀疏正则化方法优于l2正则化方法，由 2种方法的近点映射算子的比较可知，组稀疏正则化方法相当于一种自适应的l2正则化方法[21]，本文实验结果也验证了组稀疏正则化方法这一优势。此外对比表2和表1的结果，总体而言，在各种自适应数据量下，组稀疏正则化方法仍不及λ1正则化方法。

表2 组稀疏和稀疏组正则化自适应算法的实验结果（正识率）（%）（括号内单个数字表示平均稀疏度，2个数字表示()）

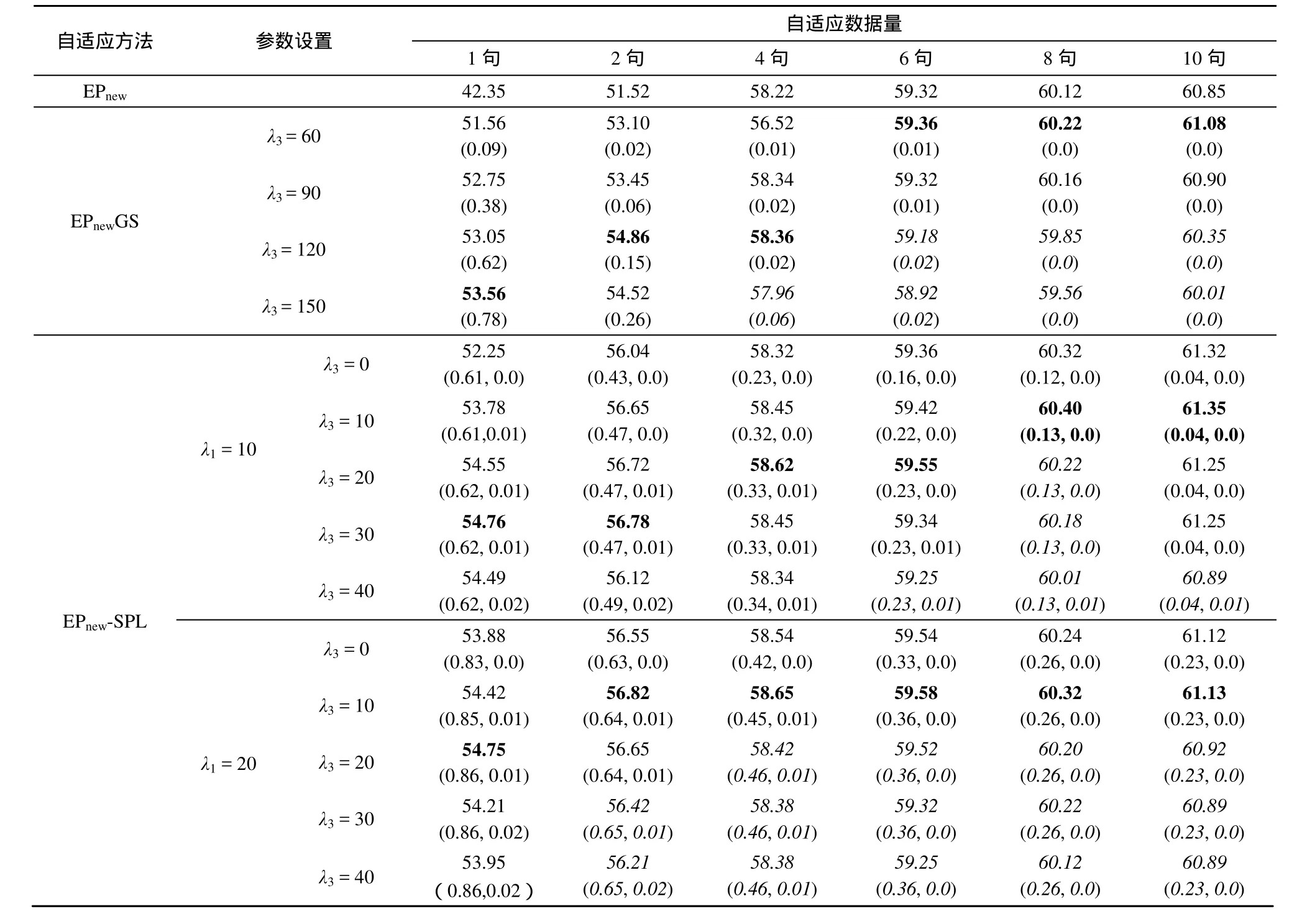
表2 组稀疏和稀疏组正则化自适应算法的实验结果（正识率）（%）（括号内单个数字表示平均稀疏度，2个数字表示()）

自适应方法 参数设置自适应数据量1句 2句 4句 6句 8句 10句EPnew 42.35 51.52 58.22 59.32 60.12 60.85 EPnewGS λ3 = 60 51.56(0.09)53.10(0.02)56.52(0.01)59.36(0.01)60.22(0.0)61.08(0.0)60.35(0.0)λ3 = 150 53.56(0.78)60.90(0.0)λ3 = 120 53.05(0.62)λ3 = 90 52.75(0.38)53.45(0.06)58.34(0.02)59.32(0.01)60.16(0.0)54.86(0.15)58.36(0.02)59.18(0.02)59.85(0.0)54.52(0.26)57.96(0.06)58.92(0.02)59.56(0.0)60.01(0.0)λ3 = 0 52.25(0.61, 0.0)56.04(0.43, 0.0)58.32(0.23, 0.0)59.36(0.16, 0.0)60.32(0.12, 0.0)61.32(0.04, 0.0)λ1 = 10 λ3 = 10 53.78(0.61,0.01)61.35(0.04, 0.0)λ3 = 20 54.55(0.62, 0.01)56.65(0.47, 0.0)58.45(0.32, 0.0)59.42(0.22, 0.0)60.40(0.13, 0.0)61.25(0.04, 0.0)λ3 = 30 54.76(0.62, 0.01)56.72(0.47, 0.01)58.62(0.33, 0.01)59.55(0.23, 0.0)60.22(0.13, 0.0)61.25(0.04, 0.0)λ3 = 40 54.49(0.62, 0.02)56.78(0.47, 0.01)58.45(0.33, 0.01)59.34(0.23, 0.01)60.18(0.13, 0.0)EPnew-SPL 56.12(0.49, 0.02)58.34(0.34, 0.01)59.25(0.23, 0.01)60.01(0.13, 0.01)60.89(0.04, 0.01)λ3 = 0 53.88(0.83, 0.0)56.55(0.63, 0.0)58.54(0.42, 0.0)59.54(0.33, 0.0)60.24(0.26, 0.0)61.12(0.23, 0.0)λ3 = 10 54.42(0.85, 0.01)61.13(0.23, 0.0)λ3 = 20 54.75(0.86, 0.01)56.82(0.64, 0.01)58.65(0.45, 0.01)59.58(0.36, 0.0)60.32(0.26, 0.0)λ1 = 20 60.92(0.23, 0.0)λ3 = 30 54.21(0.86, 0.02)56.65(0.64, 0.01)58.42(0.46, 0.01)59.52(0.36, 0.0)60.20(0.26, 0.0)60.89(0.23, 0.0)λ3 = 40 53.95（0.86,0.02）56.42(0.65, 0.01)58.38(0.46, 0.01)59.32(0.36, 0.0)60.22(0.26, 0.0)56.21(0.65, 0.02)58.38(0.46, 0.01)59.25(0.36, 0.0)60.12(0.26, 0.0)60.89(0.23, 0.0)

由于组稀疏正则化与λ1正则化具有互补性，表2给出了稀疏组LASSO约束的结果。结果表明，在λ1正则化基础上引入组稀疏正则化后，自适应性能得到进一步提高，特别是当自适应数据量较少时（1或 2句话），性能的提高尤为明显。例如，当λ1= 1 0,λ3= 3 0时，相比于λ1=10时的λ1正则化方法，在1句话和2句话下，正识率分别相对提高了4.8%和1.3%。在正则化因子λ1固定的条件下，随着自适应数据量的增加，应减少正则化因子λ3以获得更好的识别效果。

从“平均稀疏度”与“平均列稀疏度”上看，引入组稀疏正则化后，平均稀疏度相对于仅采用λ1正则化时的值几乎没有变化，而平均列稀疏度都基本接近于零，这说明最终估计得到的扩展本征音子矩阵并没有呈现出明显的列稀疏性。对比表 2中的实验设置，可以看出由于组稀疏正则化因子λ3相对较小，而其对应的近点映射算子为一种乘性收缩算子，因此只能使某些列的值相对缩小，却难以将其缩小到0。

对比表 2和表 1中实验结果可见，稀疏组LASSO正则化方法明显优于弹性网正则化方法，其原因在于组稀疏正则化方法相当于一种自适应的l2正则化方法，因此其与λ1正则化的线性组合（即稀疏组LASSO正则化方法）相当于一种自适应的弹性网正则化方法。

5 结束语

本文提出了一种基于稀疏组LASSO约束的本征音子说话人自适应方法。新方法对自适应问题的目标函数引入稀疏组LASSO正则项，相当于对待估本征音子矩阵同时施加列间稀疏性约束与列内稀疏性约束，得到结构化的模型稀疏解。通过该约束可以对自适应模型的复杂度进行有效控制，在数据量少时得到低维音子变化子空间，在数据量充足时得到高维音子变化子空间。实验证明，新算法在各种自适应数据量下均优于经典的λ1正则化、l2正则化和弹性网正则化方法。

[1] ZHANG W L, ZHANG W Q, LI B C,et al. Bayesian speaker adaptation based on a new hierarchical probabilistic model[J]. IEEE Transactions on Audio, Speech and Language Processing[J]. 2012, 20(7):2002-2015.

[2] SOLOMONOFF A, CAMPBELL W M, BOARDMAN I. Advances in channel compensation[A]. for SVM speaker recognition. Proceedings of International Conference on Acoustics, Speech, and Signal Processing(ICASSP)[C]. Philadelphia, USA, 2005. 629-632.

[3] PAVAN KUMAR D S, PRASAD N V, JOSHI V,et al. Modified splice and its extension to non-stereo data for noise robust speech recognition[A]. Proceedings of IEEE Automatic Speech Recognition and Understanding Workshop(ASRU)[C]. Olomouc, Czech Republic, 2013.174-179.

[4] HAMIDI S G, RICHARD C R. Two-stage speaker adaptation in subspace gaussian mixture models[A]. Proceedings of International Conference on Acoustics, Speech and Signal Processing(ICASSP)[C].Florence, Italy, 2014. 6374-6378.

[5] WANG Y Q, GALE M J F. Tandem system adaptation using multiple linear feature transforms[A]. Proceedings of International Conference on Acoustics, Speech and Signal Processing(ICASSP)[C]. Vancouver,Canada, 2013. 7932-7936.

[6] KENNY P, BOULIANNE G, OUELLETET P,et al. Speaker adaptation using an eigenphone basis[J]. IEEE Transaction on Audio, Speech and Language Processing, 2004, 12(6):579-589.

[7] ZHANG W L, ZHANG W Q, LI B C. Speaker adaptation based on speaker-dependent eigenphone estimation[A]. Proceedings of IEEE Automatic Speech Recognition and Understanding Workshop(ASRU)[C].Hawaii, USA, 2011. 48-52.

[8] LI J, TSAO Y, LEE, C H. Shrinkage model adaptation in automatic speech recognition[A]. Proceedings of Annual Conference on International Speech Communication Association(INTERSPEECH)[C]. Makuhari, Chiba, Japan, 2010. 1656-1659.

[9] OLSEN P A, HUANG J, RENNIE S J,et al.Sparse maximum a posteriori adaptation[A]. Proceedings of IEEE Automatic Speech Recognition and Understanding Workshop(ASRU)[C]. Hawaii, USA, 2011.53-58.

[10] OLSEN P A, HUANG J, RENNIE S J,et al. Affine invariant sparse maximum a posteriori adaptation[A]. Proceedings of International Conference on Audio, Speech and Signal Processing(ICASSP)[C].Kyoto, Japan, 2012. 4317-4320.

[11] KIM Y G, KIM H. Constrained mle-based speaker adaptation withλ1regularization[A]. Proceedings of International Conference on Audio,Speech and Signal Processing(ICASSP)[C]. Florence, Italy, 2014.6419-6422.

[12] 张文林, 张连海, 牛铜, 等. 基于正则化的本征音说话人自适应方法[J]．自动化学报, 2012, 38(12):1950-1957.ZHANG W L, ZHANG L H, NIU T,et al. Regularization based eigenvoice speaker adaptation method[J]. ACTA Automatica Sinica,2012, 38 (12):1950-1957.

[13] YOUNG S, EVERMANN G, GALES M,et al. The HTK book (for HTK version 3.4)[EB/OL]. http://htk.eng.cam.ac.uk/docs/docs.shtml.2009.

[14] 张文林, 张连海, 陈琦, 等. 语音识别中基于低秩约束的本征音子说话人自适应方法[J]. 电子与信息学报, 2014, 36(4):981-987.ZHANG W L, ZHANG L H, CHEN Q,et al. Low-rank constraint eigenphone speaker adaptation method for speech recognition[J]. Journal of Electronics & Information Technology, 2014, 36(4):981-987.

[15] YUAN M, LIN Y. Model selection and estimation in regression with grouped variables[J]. Journal of the Royal Statistical Society(Series B),2007, 68(1): 49-67.

[16] TAN Q F, NARAYANAN S S. Novel variations of group sparse regularization techniques with applications to noise robust automatic speech recognition[J]. IEEE Transaction on Acoustic, Speech and Signal Processing, 2012, 20(4):1337-1346.

[17] SIMON N, FRIEDMAN J, HASTIE T,et al. A sparse-group LASSO[J]. Journal of Computational and Graphical Statistics, 2013, 22(2):231-245.

[18] CHANG E, SHI Y, ZHOU J,et al. Speech lab in a box: a Mandarin speech toolbox to jumpstart speech related research[A]. Proceedings of 7th European Conference on Speech Communication and Technology(EUROSPEECH) [C]. Aalborg, Denmark, 2001. 2799-2802.

[19] BECK A, TEBOULLE M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(1):183-202.

[20] BERTSEKAS D P. Incremental proximal methods for large scale convex optimization[J]. Mathematical Programming, 2011, 129(2):163-195.

[21] PARIKH N, BOYD S. Proximal Algorithms. Foundations and Trends in Optimization[M]. 2013.