一种基于分割的立体匹配算法
孙东亮,余贞侠,魏 敏
(成都信息工程学院计算机学院,四川成都610225)
0 引言
当人们逐渐意识到“视觉应该是简单的事情”是一种误解时,对计算机视觉的研究也成为独立的研究领域,而关于立体匹配的主题作为这一领域研究最广和最基础的问题之一,仍是最活跃的研究方向之一。立体匹配过程尝试寻找两幅或者多幅图像间的匹配像素点,然后将它们的2D位置转化为3D深度,从而可以估计出场景的一个3D模型,这使立体匹配成为众多研究方向的基础,例如摄影测地学关注的航空影像、人视觉系统建模、视图差值和基于图像渲染等。
Scharstein和Szeliski[1]将稠密立体匹配算法分为局部算法和全局算法两部分。局部(基于窗口的)算法主要针对图像每个像素点,在局部有限窗口内计算其亮度差异等代价函数,并以窗口内聚合后具有最小代价的视差作为最佳视差。Tomvari,Mattoccia等[2]比较的所有局部聚集方法中,Yoon与 Kweon[3]的局部加权方法在平衡性能和速度两方面具有突出的效果。全局算法通常不进行聚集操作,而是在初步得到视差值后,最小化一个包含数据项和平滑项的全局代价函数,不同算法间的主要区别在于使用的寻找最小值过程。其中基于动态规划的算法,图割的算法,基于置信度传播的方法等均取得很好的效果。
基于分割的立体匹配算法,主要是基于场景分段平滑性假设,根据色彩和边界信息将场景分割为一系列区域,并尝试给每个区域标记一个视差。Tao等[4]首先利用局部的方法估计逐像素的视差,然后将图像的分割结果应用到匹配过程中,使用一个平面模型表示每个分割区域,最后加入相邻区域的平滑性约束,以全局匹配能量最小化的形式精化得到视差。在Tao等提出的框架基础上,发展了非常多的基于图像分割的立体匹配算法,并且取得不错的效果[5-11]。
1 算法设计
提出的基于分割的立体匹配算法,使用均值漂移算法进行图像的分割,改进Yoon等的算法进行初始视差图的求取,并使用两次不同的能量函数对平面模板参数进行求取与最优选择。具体流程如图1所示。

图1 算法流程图
1.1 图像分割
均值漂移(Mean Shift)算法[12]的实质是核密度估计,核心是对特征空间的样本点进行聚类,应用到彩色图像分割中就是对图像的色彩信息进行聚类,以不同的色彩类表示不同的物体。在具体实现中如文献[12]所表述,将图像看作是五维向量,其中颜色信息占3个分量,像素位置信息占2个分量,其核函数的具体形式为
其中hs、hr为控制空间域和颜色域的平滑解析度,C为归一化常数。
以Middlebury大学计算机视觉研究室网站的标准测试数据“Tsukuba”图作为研究对象,Tsukuba在左视点的图像如图2所示,设置参数hs=7,hr=5.6,分割区域最小像素个数为20,以文献[12]的方法对Tsukuba图进行分割得到分割结果如图3所示。

图2 Tsukuba左视图

图3 Tsukuba分割图
1.2 基于自适应权值的匹配及双向检测
1.2.1 基于自适应权值的匹配
Yoon和Kweon从人类视觉出发,利用格式塔心理学的接近性原则和相似性原则设计窗口匹配加权系数,这个权值由两个像素间的空间相近性和颜色相似性计算得来,所以权值大小具有自适应性,其计算方式为

其中Δ cpq和Δ gpq分别为p和q两个像素点间的颜色差异和空间距离差异,k为比率常数。其中颜色差异是在CIELab颜色空间下计算得到,空间距离差异由两个像素之间空间距离作为度量,又由于颜色接近性和空间接近性是相互独立的,且选取了基于拉普拉斯核函数的权值度量,于是有
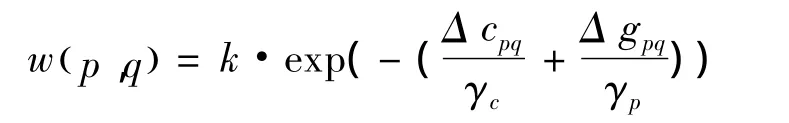
其中γc和γp分别为颜色差异参数和距离差异参数。设p是左视点图中的像素,pd是视差为d时p点在右视点图中的对应像素,那么相关窗内的匹配代价累计公式为

其中q是在左视点图中p的相关窗内的像素,而qd是在右视点图中pd的相关窗内的像素
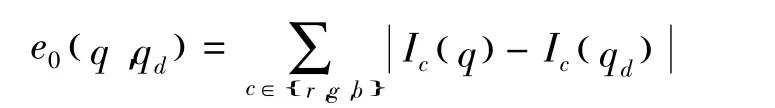
最后在一定视差范围内,对每个像素采用赢者通吃(winner-take-all,WTA)策略选择使累计代价 E(p,pd)最小的d值作为其视差。
文献[13]对此方法进行详细的分析,并提出利用分割结果,对同一区域内的两个像素点将距离权值设为1,从结果看修正了原方法的很多错误,所以文中方法也借鉴此改进,将像素点p和q之间的权值度量方法更改为

仍然以“Tsukuba”图作为实验对象,设置参数如下:窗口大小31×31,比率常数k=1.0,颜色差异参数γg=7.0,空间距离差异参数γc=36.0,视差浮动范围0~15。需要注意的是,结果图中便于观察,所有视差图中的视差值均乘16,以左视点图像为参考图,右视点图像为匹配图,得到左视点图像的视差图如图4所示。

图4 Tsukuba初始视差图
1.2.2 双向检测
可以看到在WTA策略下每个像素一定会得到一个在匹配代价准则下的最优视差值,然而对于图像内的遮挡区域的像素,其在一幅图中可见而在另一幅图中不可见,是不应该找到最佳匹配的。
双向检测可以准确地找到不可信视差值,具体实现方式是,首先利用基于自适应权值的方法分别将左右视图看做参考图得到各自的视差图,然后定义一个错误允许值Tc(Tc≥1),以左视差图为参考,遍历左视差图的所有像素点,在每一点(x,y)处的视差值为dL(x,y),可以得到匹配图右视差图中坐标为 (xdL(x,y),y)处的视差值dR(x- dL(x,y),y)。认定当满足

则认为左视差图中坐标为(x,y)处的视差值是可信的,不然就将该坐标处的视差值置为不可信,用视差0进行填充标记,遍历完成得到可信的左视差图,如图5所示。
依据相同的原理,以右视差图为参考图像,遍历右视差图的所有像素点,在每一点(x,y)处的视差值为dR(x,y),可以得到匹配图右视差图中坐标为 (x+dR(x,y),y)处的视差值dL(x+dR(x,y),y)。当满足
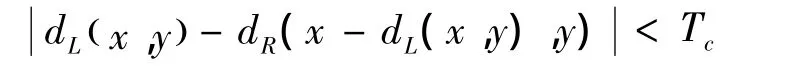
则认为右视差图中坐标为(x,y)处的视差值是可信的,不然就将该坐标处的视差值置为不可信,用视差0进行填充标记,遍历完成得到可信的右视差图。

图5 Tsukuba双向检测后视差图
1.3 平面模型求取与优化
在场景分段平滑性假设中,对于区域内平滑过渡的视差可以通过拟合平面或曲面的方法计算分块内的视差。平面或曲面模型能较好的改善无纹理区域在局部匹配下的错误,对于遮挡区域可以认为是相邻可见区域视差的光滑过度,从而可以利用拟合得到的视差平面直接计算得到遮挡区域的视差值。
1.3.1 基于局部评价函数的遗传算法求取可信区域平面模型
最小二乘法是平面拟合中最常用的方法,其本质是求取均方代价最小问题,体现的是全局最优性,但是其对奇异值非常敏感,对最终结果的影响较大。遗传算法是一种模拟自然进化过程搜索最优解或次优解的方法,主要包括编码初始化、种群评价、选择、交叉、变异等步骤[14]。
借鉴全局匹配中能量最小化框架,首先为每个区域i定义一个能量函数

这个能量函数包括两部分,其中第一部分为数据能量被定义为

其中VL、VR分别代表左右图当前区域可见像素,像素pd与像素p为一对儿匹配像素,pd由p在当前平面参数下求得的视差d计算而来,r、g、b代表像素颜色分量。
第二部分为遮挡能量,λocc表示遮挡惩罚常量,Eocclude是区域内当前平面参数下求得的视差值,经双向检测后不满足条件的像素个数。
可以看到,这个能量函数的数据能量部分,用相对应的像素色彩差异反映了区域内像素在所选视差下的匹配准确程度,而遮挡能量则反映遮挡现象引起的错误对匹配的影响,所以要做的就是寻找能够使能量函数最小的视差平面,这样得到的结果才具有高的匹配精度。
具体实现步骤如下:
编码初始化:这里采用实数编码,将平面参数看作是遗传因子,每一条染色体就是一组平面参数。首先对有足够可信点的分割区域,随机选取可信点由最小二乘法获取一组平面参数作为一条染色体,重复N次得到一个大小为N的初始种群;
种群评价:以Ei作为区域的评价函数,对每条染色体进行评价获得适应度值;
选择:选用轮盘赌策略依据最适应概率选择进行交叉的染色体;
交叉:在一定交叉概率下进行交叉操作,交叉操作选用均匀交叉算子即在满足一定概率的情况下对相对应的基因进行交叉,由此可得到两条新的染色体;
生成新的种群:迭代进行选择和交叉步骤后可得到一个新的种群,对新的种群进行适应度值评价后,将当前最好染色体替代新种群中最差染色体保存在当代种群中;
最后将种群中最佳平面参数作为得到的区域平面模型。
1.3.2 优化区域平面模型
对于图像中区域过小或者因双向检测后可信视差值不足的区域,可以使用已经得到的平面模型,依据使能量函数最小的策略,为它们选择一个最适应的平面模型。
这里重新定义能量函数,在原有能量函数的基础上增加了平滑项能量,平滑能量反映出相邻像素间视差的变化差异,使它最小则可以保证区域内像素的平滑过渡。重写能量函数如下所示
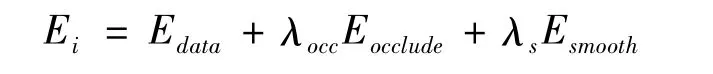
其中第三部分为平滑能量,λs表示平滑惩罚常量
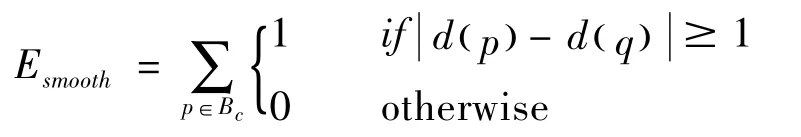
其中Bc为当前区域边界的可见点集合,q为p的4邻域可见像素。
2 实验结果和分析
为检验提出的算法的效果,在VS2010上编程对算法进行实现,展示的结果图为对测试平台(http://vision.middlebury.edu/stereo)内的数据之一 Tsukuba场景图的处理结果。初始视差求取时参数为窗口大小31×31而颜色差异参数为γc=7,距离差异参数为γp=30,而在能量函数中遮挡惩罚常量为λocc=20,平滑惩罚常量为λs=10,平面拟合是可信区域需最少具有100个可信点,遗传算法中种群大小为50,交叉概率为0.5,均匀交叉算子内交叉概率为0.5,迭代次数为20。在这些参数下对图5所示的视差图,进行平面模型的求取与优化步骤,得到如图6所示的Tsukuba的最终视差图,另外从Middlebury网站上获取Tsukuba图的真实视差图如图7所示,于是得到文中算法得到的视差图与真实视差图相比发生错误的地方,如图8所示。
文中算法是在经过校对的标准双目系统下对获取到的图片进行处理的,在标准测试平台提供的测试数据集下,上传处理结果经过在线测试得到的误匹配率结果如表1所示,其中包括 Tsukuba、Venus、Teddy和Cones 4个场景图,并将每个场景图下的非遮挡区域误匹配率、整体误匹配率和视差边缘处误匹配率作为评价标准。在与 Scharstein和 Szeliski提出的图割(Graph-cut,GC)算法和动态规划(Dynamic programing,DP)算法及Qingxiong Yang提出的置信度传播(Belief-propagation,BP)算法[15]的比较中,可以看到文中算法在视差不连续区域,及无纹理区域的视差求取的视差具有相对较高的准确度,但是从图8所示的误匹配图及图2所示的分割结果图中可以分析出,由于分割错误造成的区域边界的视差结果错误,文中算法并没有很好的解决这一问题。

图6 Tsukuba最终视差图

图7 Tsukuba的真实视差图

图8 Tsukuba的错误匹配图

表1 误匹配率结果对比
3 结束语
在图像分割的基础上提出一种新的立体匹配算法。首先使用mean-shift算法对左右原始图像进行分割,再利用局部的基于窗的自适应权值的方法得到初始视差图,经双向检测后对可信区域采用基于能量函数最小化的遗传算法进行平面拟合,并经平面模型再分配过程得到最终的视差图。实验结果表明,文中算法可以有效地处理深度不连续区域,及无纹理区域匹配精度高,得到了更为准确的稠密视差图。但是从结果中也看到,对于分割错误造成的像素点的错误匹配仍有提高的余地。
致谢:感谢成都信息工程学院人才基金(J201212)对本文的资助
[1] Scharstein D,R Szeliski.A Taxonomy and Evaluation of Dense Two-Frame Stereo Correspondence Algorithms[J].International Journal of Computer Vision,2002,47(1-3):7-42.
[2] Tombari F.Classification and evaluation of cost aggregation methods for stereo correspondence[C].in ComputerVision and Pattern Recognition,CVPR 2008.IEEE Conference on,2008.
[3] Kuk-Jin Y,K In-So.Locally adaptive supportweight approach for visual correspondence search[C].in Computer Vision and Pattern Recognition,CVPR 2005.IEEE Computer Society Conference on,2005.
[4] Hai T,H S Sawhney,R Kumar.A global matching framework for stereo computation.in Computer Vision[C].ICCV 2001.Proceedings.Eighth IEEE International Conference on,2001.
[5] Zeng-Fu W,Z Zhi-Gang.A region based stereo matching algorithm using cooperative optimization[C].in Computer Vision and Pattern Recognition,CVPR 2008.IEEE Conference on,2008.
[6] Klaus A,M Sormann,K Karner.Segment-Based Stereo Matching Using Belief Propagation and a Self-Adapting Dissimilarity Measure[C].in Pattern Recognition,2006.ICPR 2006.18th International Conference on,2006.
[7] Yang Q.Stereo matching with color-weighted correlation,hierarchical belief propagation,and occlusion handling[J].IEEE Trans Pattern Anal Mach Intell,2009,31(3):492-504.
[8] 郑志刚,高精度摄像机标定和鲁棒立体匹配算法研究[D].合肥:中国科学技术大学,2008.
[9] Zitnick C L,Kang S B,Uyttendaele M,et al.High-quality video view interpolation using a layered representation[J].ACM Transactions on Graphics(Proc.SIGGRAPH 2004),2004,23(3):600-608.
[10] Zitnick C L,Kang S B.Stereo for image-based rendering using image over-segmentation[J].International Journal of Computer Vision,2007,75(1):49-65.
[11] Taguchi Y,Wiburn B,Zitnick C L.Stereo reconstruction with mixed pixels using adaptive oversegmentation[C].IEEE Computer Society Conference on Computer Vision and Pattern Recognition(CVPR 2008),2008.
[12] Comaniciu D,P Meer.Mean shift analysis and applications[C].in Computer Vision,1999.The Proceedings of the Seventh IEEE International Conference on,1999.
[13] Tombari F,S Mattoccia,L Stefano.Segmentation-Based Adaptive Support for Accurate Stereo Correspondence,in Advances in Image and Video Technology[M].Springer Berlin Heidelberg.
[14] Chaiyaratana N,A M S Zalzala.Recent developments in evolutionary and genetic algorithms:theory and applications[C].in Genetic Algorithms in Engineering Systems:Innovations and Applications,1997.GALESIA 97.Second International Conference On(Conf.Publ.No.446),1997.
[15] Qingxiong Y,W Liang,N Ahuja.A constantspace beliefpropagation algorithm forstereo matching[C].in Computer Vision and Pattern Recognition(CVPR),2010 IEEE Conference on,2010.

