基于矢量分析的DOA估计
王海江,刘玟宏,罗 文
(成都信息工程学院电子工程学院,四川成都610225)
0 引言
雷达发射出去的信号碰到目标,目标就会对发射信号进行调制并反射回来,称为回波信号,目标的全部信息都蕴藏在这个回波信号内。检测分析回波信号内的信息,就能获得有关目标的各个参数。将目标近似看成点目标时,一般认为目标中包含的信息是方位、仰角、距离、速度及回波强度,但不能检测出有关目标性质如外形结构等参数。随着雷达的测量精度不断提高,当测量精度接近于目标尺寸时,目标的几何形状、尺寸、在空间的取向等会对回波产生某种程度的调制,此时发生质的变化,已不能单纯把目标看成一个点[1]。具体地说,由于雷达发射信号总是以某种极化形式发射出去,目标的几何形状、尺寸、在空间的取向这类信息将通过极化调制的形式从目标的回波中带回来[2]。测得的目标的极化信息中包含大量与目标形状、结构、尺寸、表面粗糙度、对称性等相关信息,通过提取回波信号中目标极化信息,就能完整地将目标的一些特征描述出来。因此,研究目标回波的极化调制、极化参数与目标特性之间关系,对雷达目标进行识别具有重要的意义[3-5]。
传统的阵列信号处理在实现电磁波信号波达方向(DOA)估计时通常仅考虑信号在空域或时域的特性,而忽略了信号的另一重要特征——信号的极化状态[6-9]。极化状态是电磁波本身固有的特征,它描述了电磁波的矢量运动,而且电磁波的矢量特性与其传播方向之间存在内在联系[10]。
文中研究了电磁波的极化并利用电磁波的极化信息来求取电磁波的波达方向。通过对电磁波的几何位形的描述,并进行一系列的坐标系转换,采用矢量分析方法把几何意念和代数运算密切的结合起来的算法,比较直观地将电磁波的矢量特性与其传播方向之间的联系描述出来,从而可以通过对电磁波极化的测量实现对电磁波信号的到达方向的测量。
1 极化参数表征电磁波
假设椭圆极化平面波,称之为极化平面Π。在极化平面Π上,极化椭圆的长轴沿单位向量方向,短轴沿方向,二者都是垂直于电磁波的传播方向。安排这3个单位矢量成右手螺旋系,即椭圆极化场可表示为

式中振荡相位表示为ψ=wt+k·r+δ,δ是一个无关紧要的初相位。ξ是长短轴之比,常数E代表电场强度大小,为简化符号,方便计算,在讨论中假设它等于1,在最后的结果中再乘上它就可以了。将上式表示成以复常数E为参数的形式
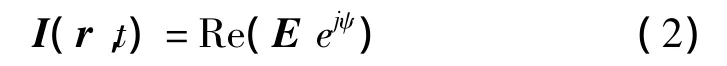
那么,式(2)可表示为

这样,就能得出复振幅向量

写成矩阵形式


写成矩阵形式

通过一种辅助天线——三维振子天线,如图1所示,这种天线具有水平全向性的特点,通过这个天线能够测到十分完整的电磁波矢量,再对这3个测出的分量进行正交解调就能够将E的实部与虚部分离出来。三维振子天线的优势集中体现在以下3个方面:(1)因为三维振子天线的同点极化分集接收方式可以用来处理宽带信号;(2)具有全向性,因此不会出现测量角度限制的问题;(3)该天线占用的空间较小,制造工艺十分成熟,且能通过3个互不相干通道对信号进行接收[11]。

图1 三维极化天线

图2 三维振子天线的三维方向图
由于三维振子天线在三维空间各个方向上都是对称的,所以其E面和H面方向图都是一致的,如图3所示。以三维振子天线作为参考系,建立与之平行的右旋坐标系,把波传播方向矢量在这个坐标系中表示出来,可得到:

其中,θ是从天线望出去信号源的仰角,φ是方位角。式中的负号表示波传波方向是由信号源指向天线。

图3 三维振子天线的平面方向图

将上式化为单位矢量,得

将式(10)、(11)和(12)合并后就能够得到如下的矩阵形式[12]
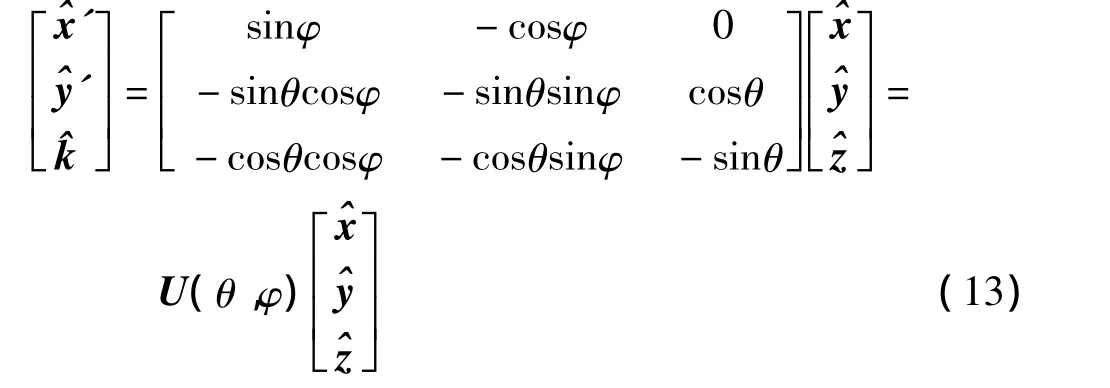
通过坐标轴各基矢量之间的变换,把式(13)代入式(8),然后再代入式(5),可以得到下面的复振幅的矩阵表示式:
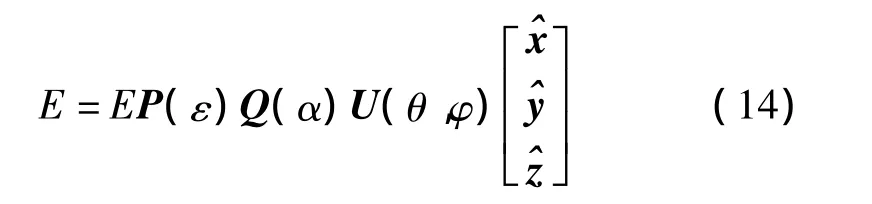
式(14)给出的是矢量表达式,取出三维振子天线上的场分量可以得到下面的行向量的表达式:
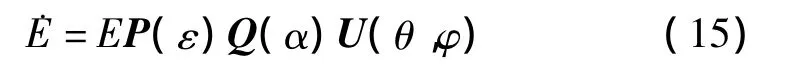
可以很容易地通过Matlab得到:

2 电磁波的极化分析
假设存在一个已知复数电场矢量e,

此处 E=Er+jEi,且 Er=Re(E)和 El=Im(E)均为实值矢量。
由于在接近地面的大气中的电场矢量散度为零,那么有
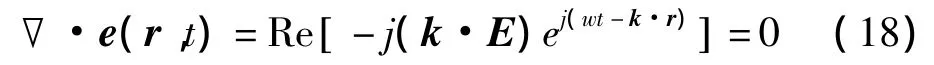
亦即k·E=0
易知电场方向始终是和电磁波的传播方向相互垂直的。除去线极化的特殊情况,首先可求出极化平面的法线n,可仿照力学里面动量矩的方式来求出电场所在极化平面的法线的方向,也就是电磁波的传播方向。

可以看出,极化平面可以通过复振幅矢量实部和虚部的矢量积来决定。
因为在地面空气中,高频电场强度的矢量的散度为零,因此它一定与电磁波传播方向是垂直的。上述矢量积在电磁波为线极化的情形下等于零。但是在实际情况中,电磁波从被发射出来在传播过程中会经过很多次的折射与反射,接收时的极化状态与发射时的极化状态已经只有较少的关联。即使最初发射的电磁波是线极化波,被接收时也已经变成椭圆极化波了。从以上讨论中,可以看出极化平面法线必定与电磁波传播方向共线,即k=±αN(α是一个正数)。
不考虑式(19)中标量对法线N方向的影响,可以得到

将上式进行分量展开,就可以得到波的传播方向方位角。


于是有
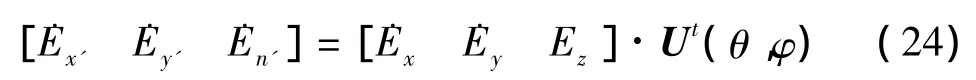

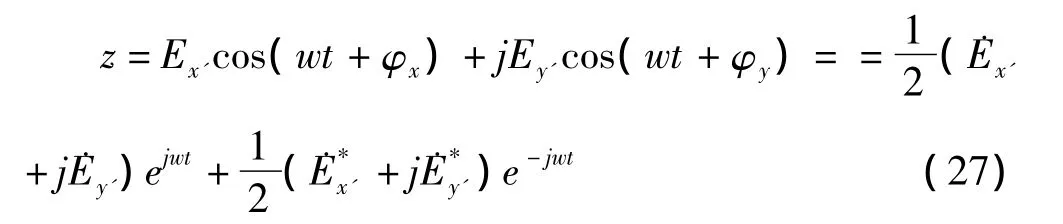
因此
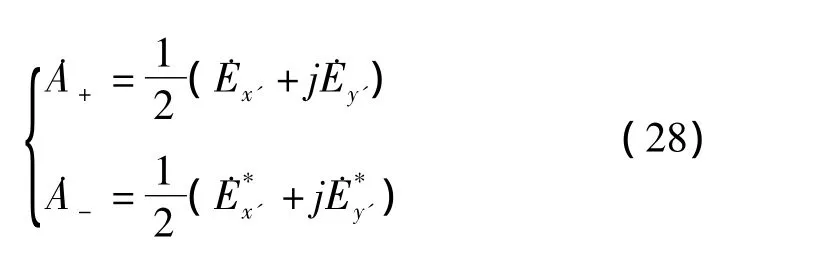
由此可得

据此写出它的辐角的正切值:

同理

可得
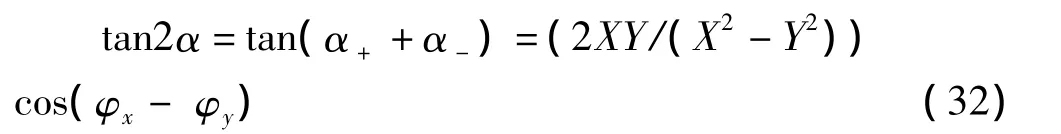
其中X=Ex';Y=Ey'。其结果与谢处方、饶克谨的《电磁场与电磁波》中列出的长轴倾斜角表达式一致。按照上述内容,可以很容易地求出极化椭圆的长、短半轴长,长轴倾斜角,以及极化平面的法线的仰角与方位角。
用矢量分析算法求取电磁波DOA方向的主要步骤是:
(1)通过三维振子天线测出完整的电波矢量,并对3个分量进行正交解调将矢量E的实部Er和虚部Ei分离开来;
(2)仿照力学里面动量矩的方式来求出电场所在极化平面的法线的方向,也就是电磁波的传播方向,即可根据式(22)求取出DOA估计方向。
3 验证算法的有效性

表1 标准试验系统结果数据在入射角为0°时测得的波达角误差
验证算法的有效性,通过多个角度,并与已知传播方向进行对比。
列出一些角度在同一信噪比的情况下,设置波数为1,信号频率为pi/4,极化椭圆[13]的长短轴及其传播方向的仰角和方位角都保持不变的情况下,其中,其长短轴之比为1∶0.3334,传播方向的仰角为10°,方位角为0°,信噪比SNR为1,测得的波达方向与给定的发射角之间的误差水平见表1。
在保持前一组数据设定的基础上,改变方位角的值,并将给定的发射角以45°进行变化,测得的波达方向与给定的发射角之间的误差水平见表2。

表2 对比数据

图4 ESPRIT算法与矢量分析算法估计偏差比较

图5 ESPRIT算法与矢量分析算法估计方差比较
选择天线阵为8阵元的均匀线阵,设置来波数为1,信号频率为pi/4,阵元间距为0.5个波长,分别选择快拍数为100和1024,入射角度保持不变,随着噪信比的增大,对ESPRIT算法与矢量分析算法所得到的估计值与实际值之间的估计误差和估计偏差进行对比,对于每一个噪信比上的估计值均选取100组数据[15],并求取数据的平均偏差和数据之间的估计方差,并根据求得的平均偏差与估计方差作图如图4和图5所示。
由图4和图5可以看出采用矢量分析算法进行DOA估计偏差与ESPRIT算法在快拍数在1024时相当,估计方差随着噪信比的增大而增大,但是从整体上看估计效果与其相似,要远优于ESPRIT算法快拍数为100时的估计效果。但矢量分析算法的优势在于算法简单,减少了大量的运算。
[1] 凌锡璜.利用雷达回波中的极化信息识别目标.大连海运学院学报,1984,(2).
[2] 曾清平,董天临,万山虎.极化雷达的发展动态与极化信息的应用前景[J].系统工程与电子技术,2003,(6).
[3] E.Korkmaz and P.van Genderen.Antenna Footprint Measurements of Stepped Frequency CW Radar on the Air-Ground Interface[J].IEEE Antenna Measurements and SAR,AMS 2004:87-91.
[4] Justin W Green,Todd B Hale,Michael A Temple,et al.IncorporatingPulse-to-PulseMotion Effects intoSide-Looking Array Radar Models[J].Fourth IEEE Workshop on Sensor Array and Multichannel Processing,2006:580-585.
[5] Lanbo Liu,Steven A,Arcone.Near-surface radar pulse propagation in complex terrain environments:preliminary results[C].10th International Conference on Ground Penetrating Radar,2004:21-24.
[6] Reinisch B W,G S Sales,D M Haines,et al.Radio wave active Doppler imaging of space plasma structures:Arrival angle,wave polarization and Faraday rotation measurements with the radio plasma imager[J].Radio Science,1999,34(6):1513-1524.
[7] Kostinski A B,Boerner W M.On foundations of radar polarimetry[J].IEEE Trans.A.P.,1986,AP-34(12):1395-1404.
[8] J J van Zyl,H A Zebker,C Elachi.Imaging Radar Polarization Signature:Theory and Observation[J].Radio Science,1987,22:529-534.
[9] Albert Guissard.Muller and Kennaugh Matrices in Radar Polarimetry[J].IEEE Trans.On GRS,1994,32(3):590-597.
[10] 董豹,姚振东.极化信息在智能天线技术中的应用[J].信号处理,2002,(12).
[11] 何敏,陈广东,张凯.从三正交偶极子天线接收信号中估计飞行器姿态参数[J].雷达学报,2012,(6).
[12] 郭仲衡.张量(理论和应用)[M].北京:科学出版社,1988.
[13] 张光义.椭圆极化波的形成和极化椭圆参数的表示[J].现代雷达,1992,(1).
[14] 黄家才,石要武,陶建武.近场源DOA、距离、极化参数及频率联合估计算法[J].计算机工程与应用,2006,(7).
[15] 何子述,夏威.现代数字信号处理及其应用[M].北京:清华大学出版社,2009:287-300.

