基于粒子滤波的制导信息提取算法研究
刘凯,梁晓庚,李友年
(中国空空导弹院 河南 洛阳 471000)
精确制导是现代武器系统的关键技术之一。精确制导系统研究包括目标探测、制导信息处理、精确定位和导航、制导算法设计和先进飞行控制系统设计等。在空空导弹的末制导中,由于导引头输出的可测制导信息非常有限,精确制导实现面临的信息缺乏问题尤为突出[1-2]。因此,如何精确的提取出关键的制导信息成为精确制导面临的一个核心问题。
制导信息估计是根据导引头的探测信息以及弹体的导航信息来解算弹目相对运动状态,比如弹目相对距离、相对速度、视线角以及视线角速率等。制导信息估计遇到的主要问题是:弹目相对运动学是严重非线性的、制导回路与所采用的制导律有关、目标探测信息不足导致估计模型可观性差。由于这些问题,解决制导信息估计精度问题一直受到广泛的重视。目前常用的制导信息提取算法主要有扩展卡尔曼滤波、跟踪滤波等[3]。
本文中,针对制导信息估计遇到的主要问题,提出了采用粒子滤波算法进行制导滤波,提取所需要的制导信息。粒子滤波是一种基于随机采样的滤波方法,主要解决非线性非高斯问题。粒子滤波的实质是递推Bayes滤波的一种实现形式,粒子滤波算法摆脱了解决非线性滤波问题时随机量必须满足高斯分布的制约条件,适用于非高斯非线性条件。
1 制导信息
制导信息提取是指依赖目标探测信息和弹体自身的导航信息来计算弹目相对运动状态,如弹目相对距离、相对速度、目标的加速度等。
考虑平面拦截情况,弹目相对运动关系如图1所示,可得弹目相对运动关系可得[4]

其中R为目标位置,R˙为相对速度,q为弹目视线角,q˙为视线角速度,vm为导弹速度、θm为弹道倾角,vt为目标速度、θt为目标速度倾角。

图1 平面拦截运动学关系Fig.1 Planar interception kinematics relations
传统的比例导引律只需要导引头输出视线角速率即可,而随着对制导精度要求的提高,出现了滑模变结构制导律、最优制导律等等,这些制导律不仅需要实现角速率信息,还需要弹目相对位置、相对速度以及目标加速度等信息,固需制导滤波算法得到弹目相对运动关系,进而求解得到视线角以及视线角速率信息。
2 粒子滤波
粒子滤波是一种基于随机采样的滤波方法,主要解决非线性非高斯问题[6]。粒子滤波实质是递推Bayes滤波的一种实现形式,在每一时刻,利用状态空间中一系列随机样本集(粒子)来近似系统状态的后验概率密度函数,从而得到下一时刻的状态估计。其主要思想是利用这些采样点和权值来获得最小方差的状态估计量,是一种基于仿真的统计滤波方法[7]。
2.1 序贯重要性采样(SIS)
从待估计的后验分布p(x0:k|y0:k)中抽样出N个独立同分布的粒子;i=1…N},则分布 p(x|y)的估计表示为0:k0:k
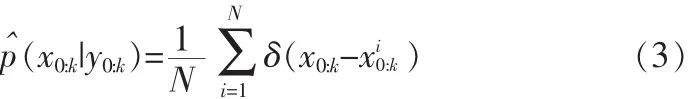
其中δ(·)为狄拉克函数。
当无法从后验分布p(x0:k|y0:k)中直接采样时,可以找一个容易采样的密度分布函数(重要性函数)q(x0:k|y0:k)中采样。则后验概率分布可以表示为

其中w(x0:k)为重要性权值,为归一化权值。
2.2 粒子滤波算法
由于在SIS算法中,离散随机量存在严重的退化问题。也就是在进行一定的迭代之后,除了很少的粒子以外,其他粒子所对应的权值都可以忽略不计。
减小退化现象的一个最有效的方法就是增大粒子数N,但N过大会给计算带来很大的负担,影响粒子滤波器的运行速度。所以考虑采用另外两种办法:1)优选重要性函数法;2)重采样法。
最优重要性函数为p(xk|xk-1,yk)。然而从最优函数中采样比较困难,一般不易求解。实际应用中更常用的是先验重要性函数:
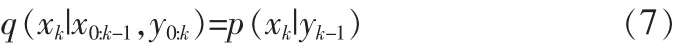
此时重要性权值的计算公式可以简化为

由于p(xk|xk-1)没有考虑观测信息 yk,所以采样得到的粒子并不能非常准确地描述后验分布。这种选取方案的优点在于根据状态方程,重要性函数的采样很容易实现,而且重要性权值也能直接由观测方程迭代计算得到。
3 制导滤波器设计
3.1 制导滤波器状态方程
导弹需要跟踪大机动目标,因此选择机动目标Singer模型对目标进行跟踪估计。该模型实质是零均值一阶时间相关模型[5],即:

其中α为机动频率,等于机动时间常数倒数,ω(t)是均值为零,方差为的白噪声,为目标加速度方差。
根据选取的目标机动模型,选取状态变量为x=[rx,ry,vx,vy,atx,aty]T,在直角坐标系下建立滤波状态方程:

其中:rx,ry弹目相对距离向量在直角坐标系中的分量;vx,vy弹目相对速度向量在直角坐标系中的分量;atx,aty为目标加速度向量在直角坐标系中的分量,amx,amy为导弹加速度;wx,wy为系统的过程噪声[8]。
3.2 目标跟踪量测方程
目标的量测信息包含实现的方位角、俯仰角和弹目视线等信号,选择观测向量为

其中R为弹目距离,θ为目标量测的方位角。并由此建立目标运动的量测方程

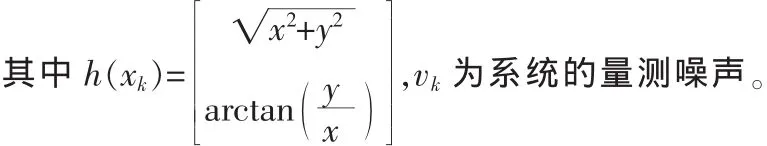
3.3 粒子滤波算法
粒子滤波算法的基本步骤如下[6]:
1)初始化:当k=0时,确认目标状态的先验概率密度函数p(x0)的表示形式,提取 N 个样本点{,i=1,…,N},并给每个粒子赋初始权重为
2)状态预测,即重要性采样、权重计算:当时刻k=1时,从转移先验密度函数通过公式为似然密度函数);
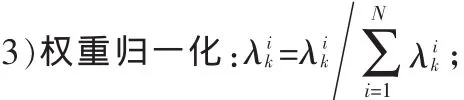

4 仿真分析
为了验证粒子滤波对于制导滤波算法的有效性,建立以下仿真模型[9],仿真参数如下:目标机动情况如下:目标的初始位置在(2 000 m,6 000 m),初始速度为(-400 m/s,0 m/s),采样间隔T=0.01 s,仿真结束时间设为stop_t=20 s,粒子滤波算法的采样粒子数N=200。
仿真过程中采用改进的导引律设计,设扩展比例导引律为:
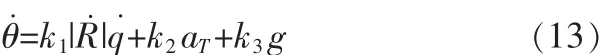
其中R˙为弹目相对速度,q˙为实现角速率,aT为目标加速度,g为重力补偿项。

图2 弹目运动关系Fig.2 Relationship between the missile and the target
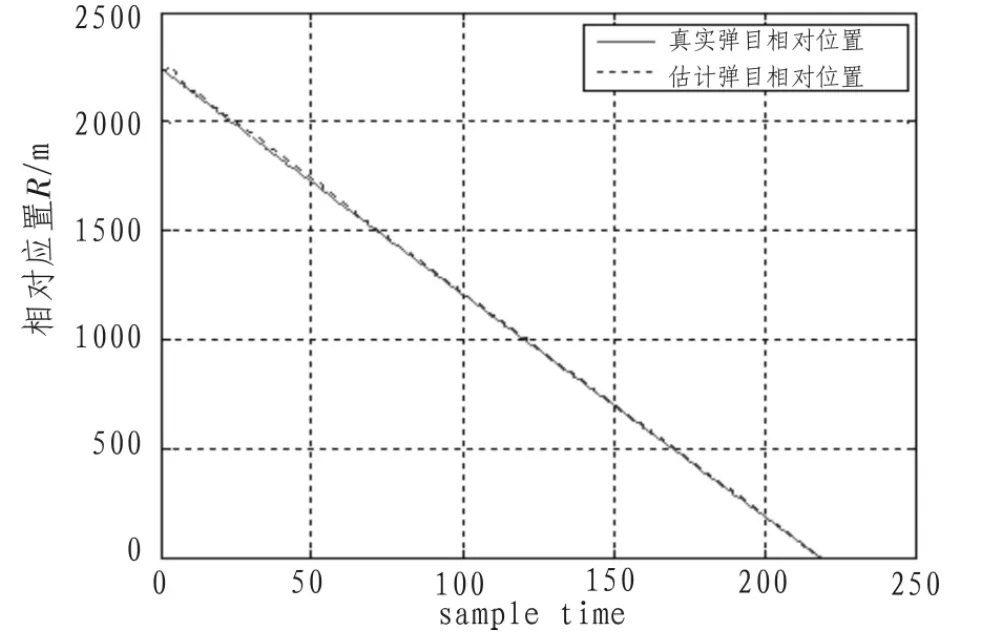
图3 弹目相对位置及估值Fig.3 Relative position and estimation between the missile and the target
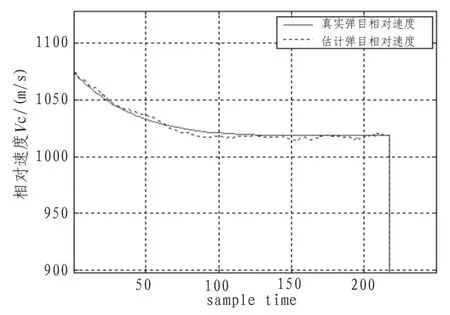
图4 弹目相对速度及估值Fig.4 Relative velocity and estimation between the missile and the target

图5 弹目视线角及估值Fig.5 Line-of-sight angel and estimation between the missile and the target
在仿真过程中,将弹体自动驾驶仪部分的传递函数近似1,进行仿真可得,仿真时间为 2.19 s,脱靶量为3.28 m,具有较高的制导精度,图1为弹目的相对运动,图2到图4分别给出了弹目相对位置、弹目相对速度、视线角和视线角速率的真实值和滤波估计值,结果表明粒子滤波对于非线性滤波具有较高的精度,验证了粒子滤波算法在制导信息提取中的有效性。
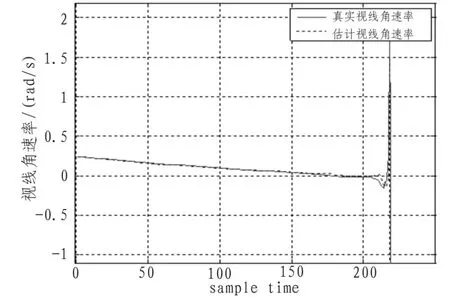
图6 弹目视线角速率及估值Fig.6 Line-of-sight angel velocity and estimation between the missile and the target
5 结束语
本文提出了采用粒子滤波进行制导信息估计,并建立仿真模型进行验证。仿真结果表明采用粒子滤波算法能够有效的估计出弹目之间的相对运动,从而提取出有效的制导信息,但是由于粒子滤波存在计算量大大、耗时长等问题,所以进一步的粒子滤波算法还有待研究。
[1]刘兴堂.导弹制导控制系统分析、设计与仿真[M].西安:西北工业大学出版社,2006.
[2]LEFASC C.Using roll-angle measurements to track aircraft maneuvers[J].IEEE Transactions on Aerospace and Electronic Systems,1984,20(6):672-681.
[3]Durbha V,Balakrishnan S N.Target Interception with Cost-Based Observer[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.21 -24 August 2006,Keystone,Colorado.AIAA 2006-6218.
[4]Paul Zarchan,Tactical and Strategic Missile Guidance[M].American Institute of Aeronautics and Astronautics,2012.
[5]周宏仁,敬忠良,王培德.机动目标跟踪[M].北京:国防工业出版社,1991.
[6]胡士强,敬忠良.粒子滤波原理及应用[M].北京:科学出版社,2010.
[7]周云端,何志勇,赵瑞国.基于遗传算法的加速度控制PID参数自整定研究[J].火箭推进,2012(4):68-71.ZHOU Yun-duan,HE Zhi-yong,ZHAO Rui-guo.Study on genetic algorithm based auto-tuning of acceleration control PID parameters[J].Journal of Rocket Propulsion,2012(4):68-71.
[8]李山峰,汤伟.循环预冷试验中测量系统干扰问题分析与措施[J].火箭推进,2014(4):77-82.LI Shan-feng,TANG Wei.Analysis and solution for interference with measurement system in cycle precooling test[J].Journal of Rocket Propulsion,2014(4):77-82.
[9]尤裕荣,袁洪滨,王春民,等.PWM高速开关阀动态调节特性仿真研究[J].火箭推进,2012(5):24-29.YOU Yu-rong,YUAN Hong-bin,WANG Chun-min,et al.Simulation of dynamic regulating characteristics of PWM high-speed on-off valve[J].Journal of Rocket Propulsion,2012(5):24-29.

