基于C语言的RSA算法的实现

戚娜

（陕西工业职业技术学院 陕西 咸阳 712000）

加密技术并不是现在才有的，它起源于公元前2000年（几个世纪了），虽然和我们现在所说的加密技术不同，但作为一种加密的概念，确实早在几个世纪前就诞生了，其目的是相同的。其都是为了保障信息在传递的过程中，防止有用或私有化信息被拦截和窃取。即使被第三方获取，没有相应的解密方法，该信息就没有任何利用价值，也就不会造成任何损失。

我们现在所说的加密技术的起源，是Diffie和Hellman于1976年在“New Direction in Cryptography”（密码学新方向）一文中首次提出了公开密钥密码体制的思想。1978年，R.Rivest，A.Shamir和L.Adleman第一次实现了公开密钥密码体制，现在称为RSA公开密钥体制[1]。迄今为止，该算法被认为是最完善最成熟的公钥密码体制，被广泛的应用于各个领域。

1 密码学基础

密码学有很长的研究历史，但一般人对它依然十分陌生，因为它只在如军事、情报、外交等这些敏感部门小范围内使用。计算机密码学是研究计算机信息加密、解密及其变换的科学，是数学和计算机的交叉学科，也是一门新兴的学科[2]。

密码技术主要用于保证电子数据的保密性，完整性和真实性。保密性是对数据进行加密，使非法用户无法读懂数据信息，而合法用户可以用密钥读取信息.完整性是对数据完整性的鉴别，以确定数据是否被非法篡改，保证合法用户得到正确、完整的信息。真实性是数据来源的真实性、数据本身真实性的鉴别，可以保证合法用户不被欺骗[2]。简单的过程如图1所示。

图1 RSA算法加密解密的过程Fig.1 Encrypt and decrypt process of the RSA algorithm

2 加密算法描述

加密算法分为两种，对称加密和非对称加密。采用对称加密时，通信的双方采用共同密钥，只需要一个密钥。不论发送方对信息的加密还是接收方对信息的解密都使用该密钥，如果该密钥在传送的过程中被第三方获取，我们给信息上所加的密钥就没有意义了。而且对称密钥如何把密钥送到对方手里，也成为了该算法的缺憾。该算法的模型如图2所示。

图2 对称密码模型Fig.2 Symmetric cipher model

与对称加密算法不同，非对称加密算法RSA需要两个密钥，一个是公开的密钥，一个是保密的私钥。它们两个成对出现，如果用公开密钥对数据进行加密，只有用对应的私有密钥才能解密；如果用私有密钥对数据进行加密，那么只有用对应的公开密钥才能解密。因为加密和解密使用的是两个不同的密钥，所以这种算法叫作非对称加密算法[3]。甲方生成一对密钥并将其中的一把作为公用密钥向其它方公开；得到该公用密钥的乙方使用该密钥对机密信息进行加密后再发送给甲方；甲方再用自己保存的另一把专用密钥对加密后的信息进行解密。甲方只能用其专用密钥解密由其公用密钥加密后的任何信息。简单流程如图2所示。

3 RSA算法的原理及应用

3.1 RSA算法的原理

RSA算法是非对称加密算法中的一种，出现于1978年。该算法是一个被广泛接受并实现的通用公开密钥加密算法，既能用于数据加密又可用于数字签名的算法之一。从提出到现在已近四十年，经历了各种攻击和考验，逐渐为人们所接受，普遍认为是目前最优秀的公钥方案之一。

图3 非对称密码模型Fig.3 Symmetric cipher model

该算法是建立在大数分解和素数检测的理论基础上，它的数学基础是初等数论中的欧拉（Euler）定理，其安全性建立在大整数因子分解的困难之上。

1）密钥的产生。首先，随机选取两个长度相同的大素数：p 和 q，另：n=p*q，另：t=（p－1）*（q－1），随机选取一个数 e，要求 e的取值范围为 （0＜e＜t）， 常用的 e值是 3，17和 65537（216+1），而且e要满足d*e%t==1，继而就可以得到d的值。这样就得到 4个数：n，t，e，d，其中 e就是加密的密钥，而 d是解密的密钥，公开 n 和 d，保密 p，q，e。

虽说加密和解密的变换是互逆的，但私钥系统把数据作为比特来处理，而公钥系统则把数据作为数字进行函数运算处理，并且这种数学函数是单向的。即在一个方向上是容易的，另一个方向上却异常困难，那么简单地颠倒步骤是无法解密密文[4]。

2）加密算法实现。 已知明文 x（x＜n），并对 x 进行分组，将x划分成字符块，使得每个明文报文xi长度m满足0＜xi＜k（其中 k 为 n 的长度），计算密文：C=xe（mod n）。

3）解密算法实现。已知密文C以及私钥（n，d），可以计算出明文 x=Cd（mod n）。

4）RSA 算法举例。 已知 p=11，q=19，得 n=209，t=180，随机选取一个数 e=7，满足 0＜e＜t，根据公式 d*e%t==1可得出d=103，d 是私有密钥。 其中公开（n，e），保密（n，d）。 假设想需要发送信息 x=65，利用（n，e）=（209，7）计算出加密值：C=xe（mod n）=657mod 209=4902227890625 mod 209=余 56， 当收到密文 C=56 后，利用（n，d）=（209，103）计算明文：x=Cd（ mod n）=56103mod 209=1.1570890445040892822428130017059…10180mod 209=65。

3.2 RSA算法的应用

3.2.1 用于交换对称加密算法的密钥

因为非对称的加密和解密算法要比对称加密和解密算法慢的多，所以非对称加密算法在实际中通常被用来安全的交换对称加密算法的密钥，而对称加密算法实际被用来作为通信过程的加密。也就是说，非对称加密算法主要用于对对称加密算法中密钥的加密。

交换对称密码的会话密钥过程如下：

1）A 用 RSA 算法生成自己的公钥（n，e）和私钥（n，d），并发送一信息给B，信息包含A的公钥（n，d）和A的标识ID。

2）B生成会话密钥K，并用 A的公钥加密后传送给A，即Kemod n。

3）A用自己的私钥解密Kemod n，即可得到K。这样，A和B就可以完全用对称加密算法和密钥K进行通信了，如图4所示。

图4 交换对称加密算法的关键过程Fig.4 Exchange of symmetric encryption algorithm key processes

3.2.2 用于数字签名

RSA算法在加密/解密过程中使用公钥加密，私钥解密。而在数字签名中则是私钥加密，公钥解密。即发送方先用HASH算法对文件M求散列值，然后利用自己的密钥对数字摘要进行加密生成数字签名C，然后将M和C一起发送给接收方。接收方接收到文件M1和数字签名C1，需要验证M和M1是否完全相同。验证过程是利用HASH函数对M1求散列值H1，利用发送方公开的公钥对数字签名C1进行解密得到H2，比较H1和H2是否相同[6]。如果相同说明信息发送安全。其具体的流程如图5所示。

4 RSA算法在C环境中的实现

4.1 程序流程图

该程序的流程图如图6所示。

图5 RSA算法在数字签名中的应用Fig.5 RSA algorithms in the digital signature

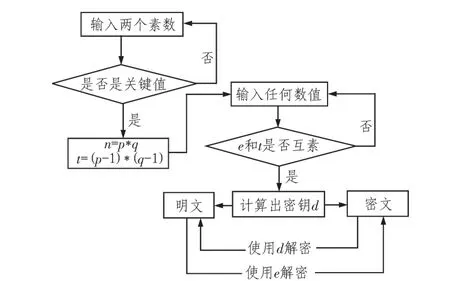
图6 程序流程图Fig.6 Flow chart

4.2 程序的相关说明

在该程序中，用户可以加密解密数字、汉字、字母等信息。在加密解密数字信息时，用户根据程序的提示，直接输入要加密解密的数字信息，即可得到该数字信息的加密或解密后的信息。对于该数字信息不需要做任何的处理，如果用户输入的是由汉字组成的信息，把汉字变成URL编码，再将URL编码转化成ASCII码进行加密解密操作.如果该信息是一个很长的字符串，就需要对加密的信息先进行分组；如果用户输入的是由字符串组成的信息，把该字符串转化成ASCII码进行加密解密操作。

该程序中，主函数主要用于根据用户输入的两个素数p和q，求n及它的欧拉数t，由用户给定的公钥e，调用子函数fun（）判断e和t是否互素，求解出私钥d。用户选择对输入的信息是加密还是解密，调用子函数my encryption（），实现了求幂取余运算，及输入信息的加密或解密运算。

寄生虫是猪常见疾病中的重要诱导因素，寄生虫能够寄生在猪的皮肤表面以及体内，进而对正常的生长产生影响，甚至在体内大量繁殖，导致猪出现疾病。面对这一现象，在此过程中需要对寄生虫展开有效防治，例如，定期组织杀虫处理，猪舍寄生虫疫苗，降低寄生虫出现的概率。另外，对猪粪便展开定期检查，如果发现粪便中含有寄生虫或者虫卵，则需要在猪饲料中添加一定的伊维菌素以及阿苯达唑粉剂，根据寄生虫的数量以及猪自身的生长情况确定用量，这种方式能够对寄生虫起到良好的控制作用，最终达到提升猪常见疾病控制质量的目的。

4.3 程序部分代码

unsigned long my encryption （unsigned long x， unsigned long y， unsigned long z）

{unsigned long r=1；

y=y+1；

while（y!=1）

{

r=r*x；

r=r%z；

y--；

}

printf（"%d "，r）；

return r；//实现幂的取余运算

unsigned long fun（unsigned long a， unsigned long b）

{

unsigned long t；

while（b）

{

t=a；

a=b；

b=t%b；

}

if（a==1）

return 0；

else

return 1；

}//判断公钥e与t是否互素

4.4 程序运行结果

当p=57，q=23时，对4573进行加密，运行结果如图7所示。

图7 程序运行结果Fig.7 The result of running

5 RSA算法的安全性

RSA算法的体制构造是基于数论的欧拉定理，它是密钥系统最安全的一种体制，其算法的安全性依赖于大数的分解。该算法利用了数论领域的一个事实，那就是虽然将两个大质数相乘生成一个合数非常容易，但要把一个合数分解成两个质数却十分困难[7]。要想对其破解需要分解一个大数，即从一个公钥中通过因数分解得到私钥就十分的困难。比如，1994年4月，为了分解RSA密钥RSA-129即分解一个129位十进制425比特的大数，600余名志愿者参加了这项破译活动，分解时启用了1 600多台工作站、大型机和超级计算机，花费了8个月的时间，终于分解了RSA－129问题中的公开钥匙。

但研究表明，自从1994年的破译工作完成之后，又有更快的因数分解计算方法提出来。因此，近年来位数较低的大数（512 bit二进制数）已被成功分解，这就告诉人们，在使用RSA算法加密时，在密钥生成时，尽量要求n很大，这样攻击者要成功的分解t=（p-1）*（q-1），就非常困难。 要使 RSA使用安全，就必须选择足够大的p和q，使用更长密钥是有益而无害的。一般选择在100位以上的十进制数字，这样攻击者没有办法在有效的多项式时间内分解出n。

6 RSA算法的缺点

1）假冒公开密钥。用户虽然不必担心公开钥匙泄密，但却需要考虑有人冒名顶替公布假的公开钥匙。所以应当尽可能地广泛地公布正确的公开钥匙，以防假冒。

2）密钥产生麻烦。由于RSA算法受到素数产生的限制，生成素数的效率比较低，因而难以做到一次一密。

3）安全性有待验证。RSA的安全性依赖于大数分解难度，但是否等同于大数分解一直未能得到理论上的证明，因为没有证明破解RSA就一定需要作大数分解。如果存在一种算法，可以快速的分解大数，那么RSA算法的安全性就会受到威胁。另外，随着计算机计算能力的不断提高，计算机造价的降低及并行技术的发展，那么攻击RSA算法能力将会得到巨大增长。

4）速度慢。使用RSA算法加密解密，要进行大量的计算，而且速度较慢，与对称密码算法相比要慢几千倍。而且随着大数分解技术的不断发展，为了保证安全，密钥的长度还要增加，计算量会更大。

7 RSA算法的发展前景

从20世纪70年代提出以来，经历了20多年的实践检验，已得到广泛的应用，成为最流行的一种加密标准。随着计算机网络和电子商务技术的不断发展，为RSA技术的应用提供了更为广阔的空间。在许多硬件，软件产品的内核中都有RSA的软件和类库，方便人们使用。比如，硬件上主要用于各类电子产品中的IC技术；软件上主要用于Internet上的加密连接、数字签名和数字认证等。另外，IE浏览器中也集成和使用了RSA技术的加密功能，结合MD5和SHA1，主要用于数字证书和数字签名，对于使用经常网购的用户来说，几乎每天都在与RSA技术打交道。但是，随着数据量的逐年增加和人们需求的不断提高，RSA面临各个方面的挑战，应用程序安全、数据安全与隐私、云安全、拒绝服务攻击、高级持续性威胁（APTs）、移动安全等，都是RSA未来几年的发展前景。

8 结 论

本文在对传统的 RSA算法[8]的原理充分研究和深刻理解上，介绍了RSA算法的主要应用，在C环境下 RSA算法的实现，并分析了RSA算法的安全性及存在的缺点。总体上来说，RSA算法是一个比较优秀的算法。但从RSA算法的应用来看，还存在很多的问题，比如公共密钥的正确性、加密解密速度很慢以及密钥产生很麻烦等。因此，在使用RSA算法时，要考虑到该算法的弱点，作好RSA算法攻击的防范。

[1]Atul Kahata.Cryptography And Network Secutrity[M].北京:清华大学出版社，2005.

[2]张仕斌，万武南，张金全.应用密码学[M].西安:西安电子科技大学出版社，2009.

[3]何彩燕，吴红.公钥制RSA算法应用中要注意的几个问题[J].现代计算机，2004，178（5）:72-74.HE Cai-yan，WU Hong.2004.Public key RSA algorithm is applied to several problems[J].Modern Computer，Volume，2004，178（5）:72-74.

[4]BUCHMANN J.A.Introduction to cryptography[M].New York:Springer-Verlage，2001.

[5]陈传波，祝中涛.RSA算法应用及实现细节[J].计算机工程与科学，2006（9）:13-14.CHEN Chuan-bo，ZHU Zhong-tao.Application of RSA algorithm and implementation details[J].Computer Engineering and Science，2009（6）:13-14.

[6]石志坚，谭全权，段海龙.RSA算法实现数字签名的研究与应用[J].微型电脑应用，2008（6）:50-51.SHI Zhi-jian，TAN Quan-quan，DUAN Hai-long.The research and application of the RSAalgorithmin thedigital signature[J].Microcomputer Applications，2008（6）:50-51.

[7]张颖，曹天人.基于RSA算法的加密应用[J].科技咨询（科技-管理），2011（25）:79-80.ZHANG Yin，CAO Tian-ren.Application of encryption based on RSA algorithm[J].Science and Technology Advisory（Technology， Administration），2011（25）:79-80.

[8]王红胜，纪道刚，张阳，等.针对RSA-CRT数字签名的光故障攻击研究[J].电子设计工程，2015（6）：12-15.WANG Hong-sheng，JI Dao-gang，ZHANG Yang，et al.Optical fault attack on RSA-CRT signatures[J].Electronic Design Engineering，2015（6）:12-15.