十五相感应电机带螺旋桨负载的矢量控制仿真研究

彭 凌，刘自程，鹿 婷，郑泽东

（1.中国舰船研究中心，武汉 430064；2.清华大学 电机工程与应用电子技术系，北京 100084）

0 引言

由于船舶电力推进系统的优越性[1]，近年来，电力推进系统在船舶上得到了广泛的应用，采用电力推进的船舶建造数目迅速增加[2]。

多相电机具有高可靠性、能容错运行、高功率密度等优点[3,4]，因而被广泛应用于需要高性能和高可靠性电机的场合，如海军舰船的电力推进系统中。

国内外对多相电机的研究多集中于五相电机与六相电机[5—8]，对于十五相电机的高性能控制的研究尚不多见。

本文研究了十五相感应电机的数学模型和仿真模型，并利用插值表建立了螺旋桨非线性负载的数值仿真模型。通过建立十五维的广义派克变换矩阵，实现了对十五相电机在四象限负载下运行的转子磁场定向矢量控制。将全系统包括十五相电机、控制器、螺旋桨负载在 MATLAB中建模，并进行了自由航行和紧急倒车两种工况下的仿真。仿真结果显示，矢量控制系统能够实现对十五相电机磁场和输出转矩的分别控制，并且确保电机在四象限下运行。

1 十五相感应电机的建模

本文研究的十五相电机的定子绕组由 3组5相绕组构成，3组绕组的中点相互隔离。当某一相绕组开路时，可以切除故障相所在整个组的 5相绕组，使电机作为十相电机继续运行；也可以改变剩余的14相绕组中电流的相位关系，以产生圆形的磁势，使电机作为十四相电机继续运行。定子绕组的位置分布关系如图1所示，3组绕组之间相差 12°电角度，每组绕组的五相绕组间相差 72°电角度。这种定子绕组结构的设计，使得基波电流产生的谐波磁势的最低次数为29次[9]。

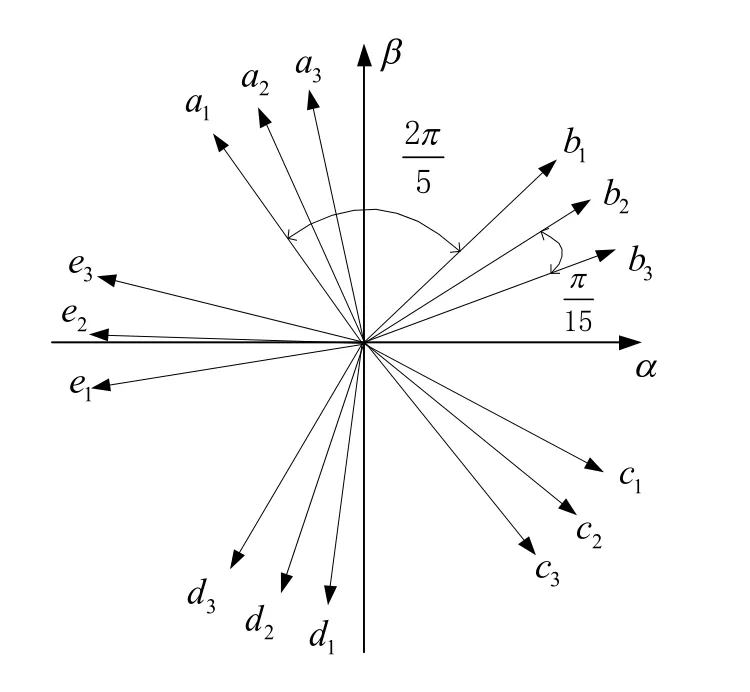
图1 定子相绕组轴线的相对位置关系

十五相感应电机的定子与转子的电压状态方程为：

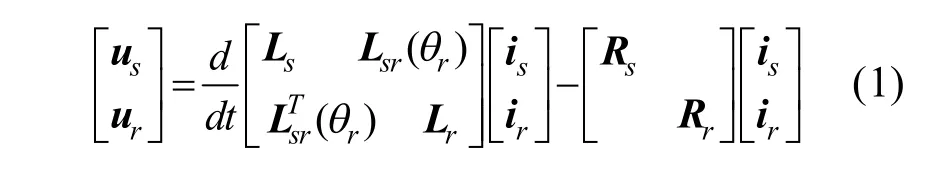
式中：Ls、Lr分别为定子绕组和转子绕组的电感；Lsr(θr)为定转子绕组间的互感；θr为转子的位置；ur,ir，分别为转子绕组的电压和电流；us,is分别为定子绕组的电压和电流，并且有：

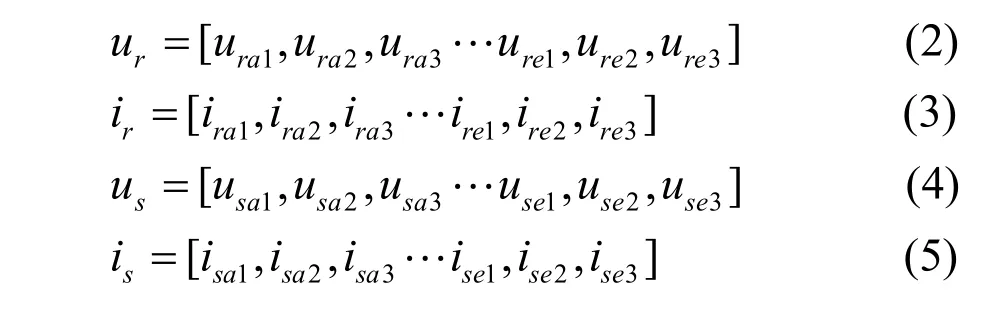
电磁转矩可以按照下式计算：

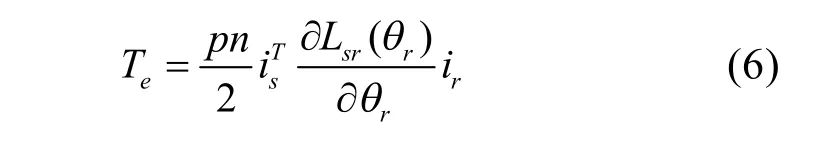
其中，pn代表转子极对数。

基于式(1)—(6)，可以由数学模型建立十五相感应电机的仿真模型。

2 螺旋桨负载的建模

在船舶的航行过程中，由于风、浪以及船舶本身的影响，螺旋桨的负载特性是复杂的。然而，本文研究的重点是电机的控制性能。因此，只需要将螺旋桨负载相比常规负载的特殊性在仿真中加以呈现。

螺旋桨的负载特性是指螺旋桨的转矩与转速之间的关系。在不同的工况下，螺旋桨的负载特性有很大差异[10]。

本文采用线性插值的方法进行螺旋桨的建模。在典型工况下螺旋桨的负载特性曲线上选择适当的点，将这些特性点输出到Simulink的查找表模块中。图2中为螺旋桨的两条典型负载特性曲线：1号曲线为自由航行特性曲线，2号曲线为紧急倒车特性曲线。

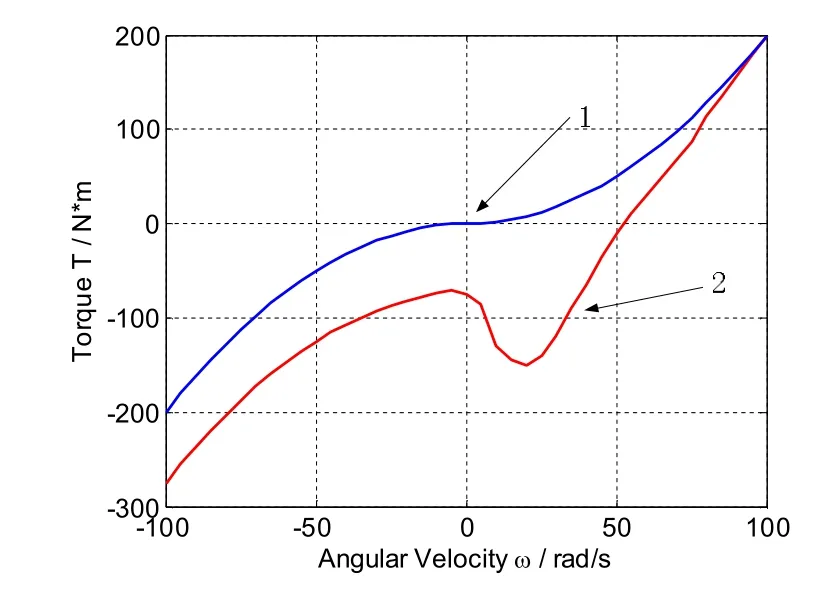
图2 螺旋桨的典型负载特性曲线

3 十五相电机的矢量控制

3.1 广义派克矩阵

对于三相电机，通过派克变换，可以将电机变换到d-q-0坐标系下。在解耦坐标系下的电机方程可以观察出，磁链与转矩可以分别控制[11]，从而可以像控制直流电机那样，对交流三相电机实现高性能的控制。

对于十五相电机，可以仿照派克变换中的d-q-0变换，将十五相向d-q轴上投影，如图3所示。可以得到十五相到d-q的变换矩阵：

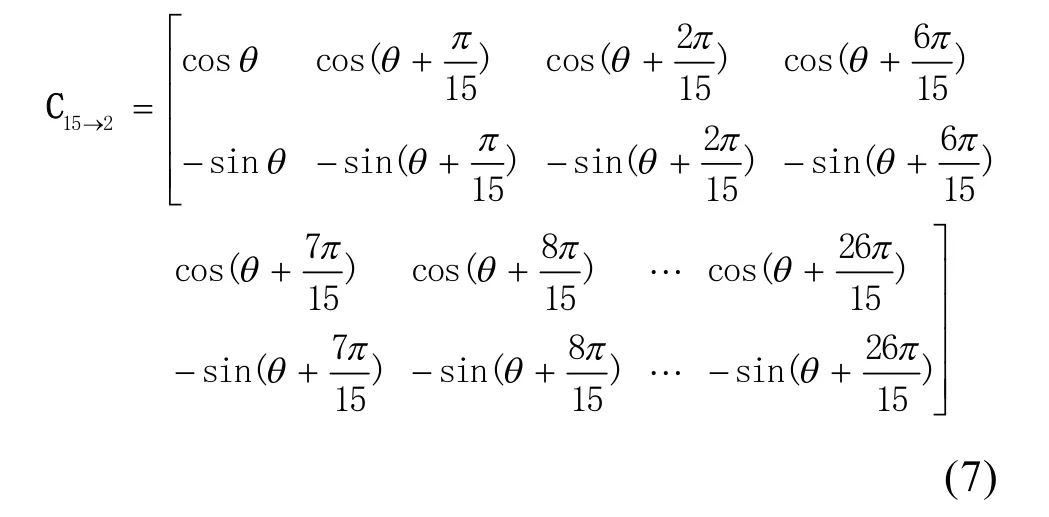
如果认为电机的中性点通过中线连接到电源的中点，十五相电机的定子绕组中就存在着15个独立电流，即可以视为15维系统。d-q-0变换选定后，应该选择另外13维的坐标变换，才能保证变换的可逆性。为了实现解耦，对剩余12维的变换要求相互正交，并且与d-q-0正交。因为d-q变换选取的是基波三角函数，为满足解耦要求，3个维度选择三套五相绕组的零序分量，剩余10维可以选择3、7、9、11、13次谐波三角函数。

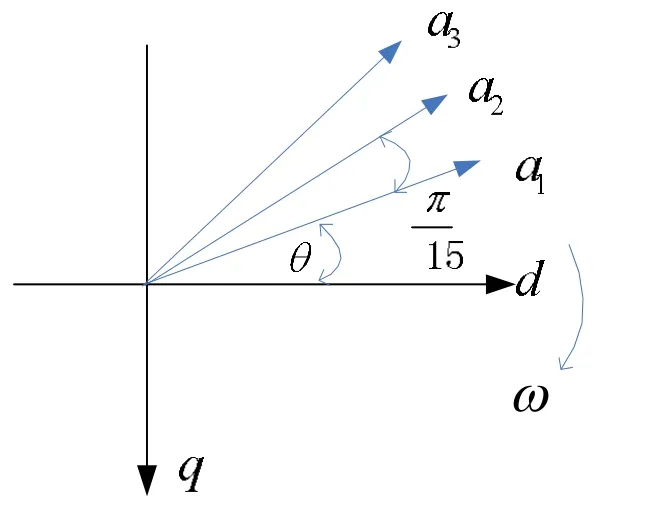
图3 十五相定子绕组的d-q轴投影

同时考虑到变换为线性变换，根据能量守恒定律，必须保证变换前后的功率不变，即：

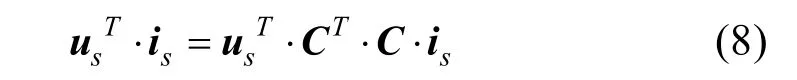
则有CT·C为单位矩阵，C为单位正交阵。

可以选取式(9)作为变换矩阵。广义派克矩阵的物理意义如表1所示[12]。

3.2 矢量控制的设计

采用广义派克矩阵对十五相电机的数学方程进行变换，可以得到新坐标系下的数学模型。因为十五相电机在基波电流供电下的最低次谐波磁动势为29次，谐波次数非常高，所以在控制时忽略高次谐波的影响，只考虑在d-q旋转坐标系(即基波平面)下的数学模型。

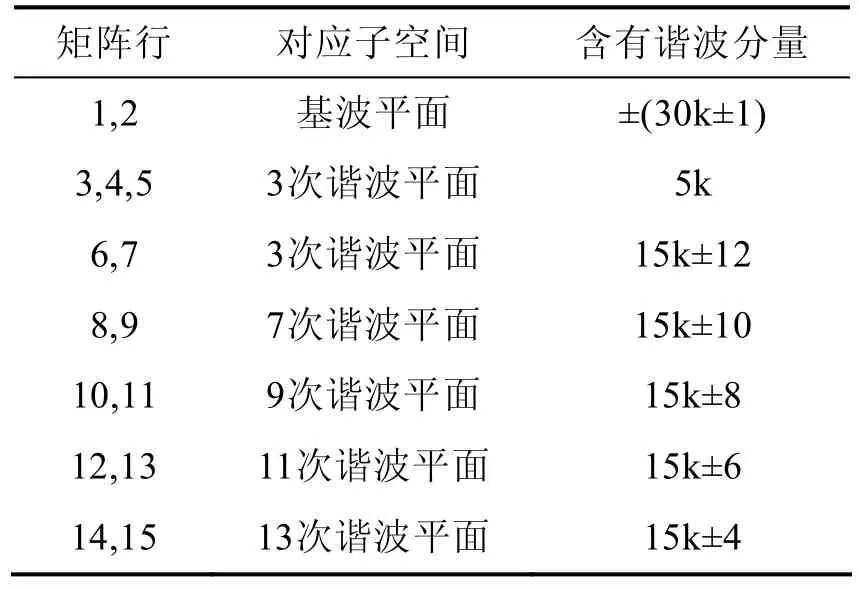
表1 广义派克变换物理意义

定转子磁链方程为：

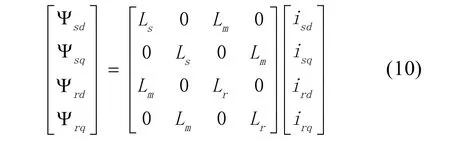
定转子电压方程为：

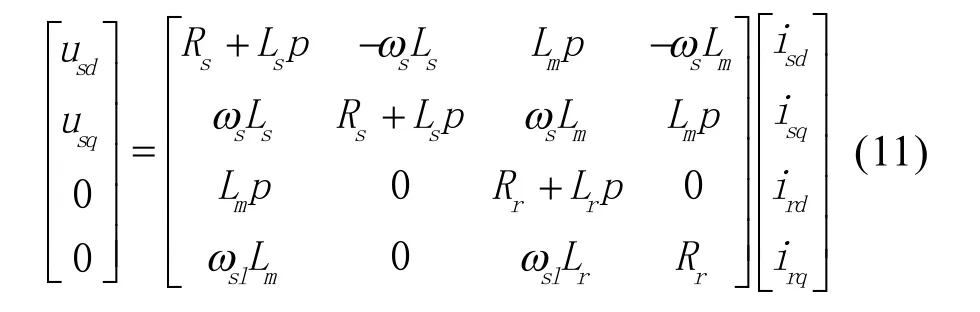
转子磁链方程为：

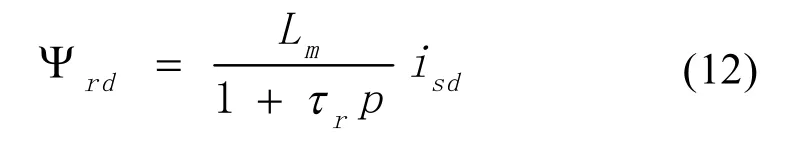
电磁转矩方程为：

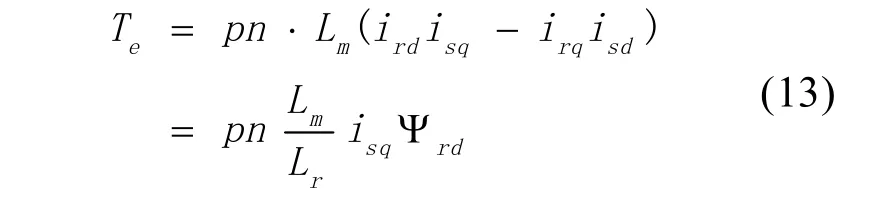
其中，Ψsd、Ψsq、Ψrd、Ψrq分别代表定子d轴磁链，定子q轴磁链，转子d轴磁链，转子q轴磁链。τr是转子时间常数，且τr＝Lr/Rr。ωsl是滑差角速度，ωs是同步角速度。p是差分算子。

由式(12)、(13)可知，电磁转矩和磁场能够分别控制。可以得到如图5所示的控制框图。

4 仿真验证

将十五相电机及其矢量控制系统，螺旋桨负载在Matlab/Simulink中建模。十五相电机的参数如表2所示。

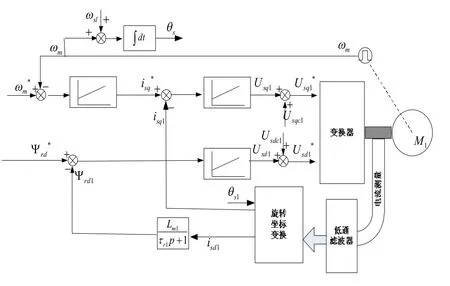
图4 十五相转子磁场定向矢量控制框图

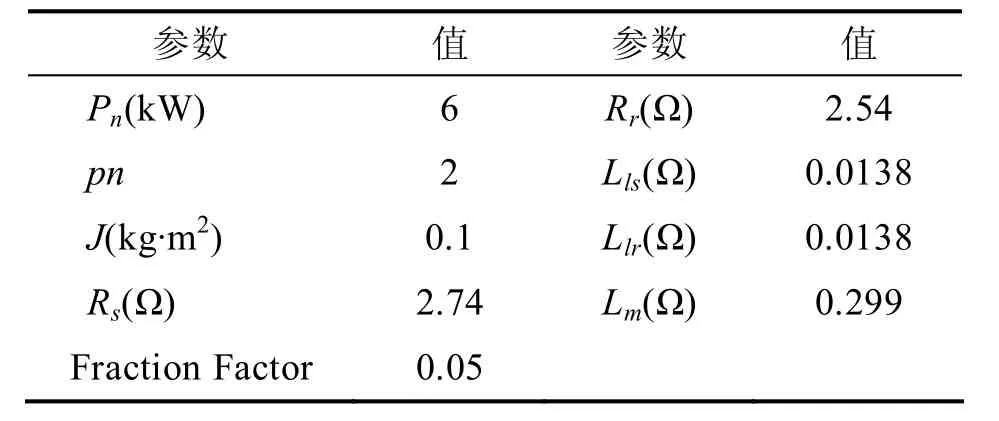
表2 十五相电机的参数

表4中：Rs是定子绕组电阻值，Rr是转子绕组电阻值，Lls是定子漏感，Llr是转子漏感。Lm是定转子互感。pn是电机的极对数。

设定仿真工况如下：从第0 s开始自由航行，由静止开始加速至额定转速(100 rad/s)；从第2 s开始，进入紧急倒车状态，由正额定转速迅速减速，反方向加速至负的额定转速(-100 rad/s)。仿真结果如下各图所示。

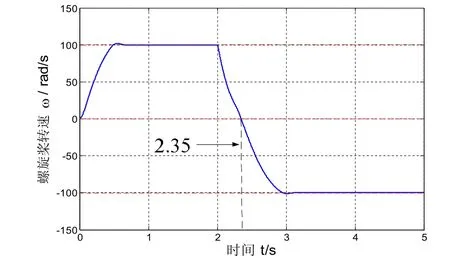
图5 螺旋桨转速

仿真结果可以看出，从第0 s起，在电机拖动下螺旋桨迅速加速，并准确稳定在额定转速。第2 s起，系统进入紧急倒车状态，电机输出的电磁转矩立即反向（图6所示），然而由于螺旋桨的非线性特性，螺旋桨转速并没有立即变负，直到第2.35s转速才反向（图7所示），因此这段过程中电机运行在发电机状态。最后，系统转速稳定在-100 rad/s。图7中的圆圈部分，说明螺旋桨模型表现出了螺旋桨的非线性负载特性。

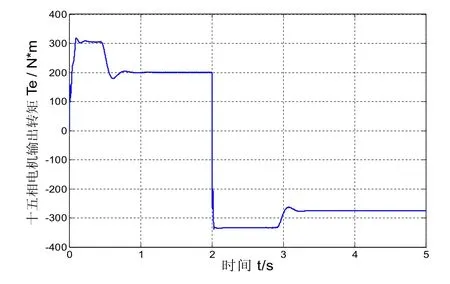
图6 十五相电机输出转矩

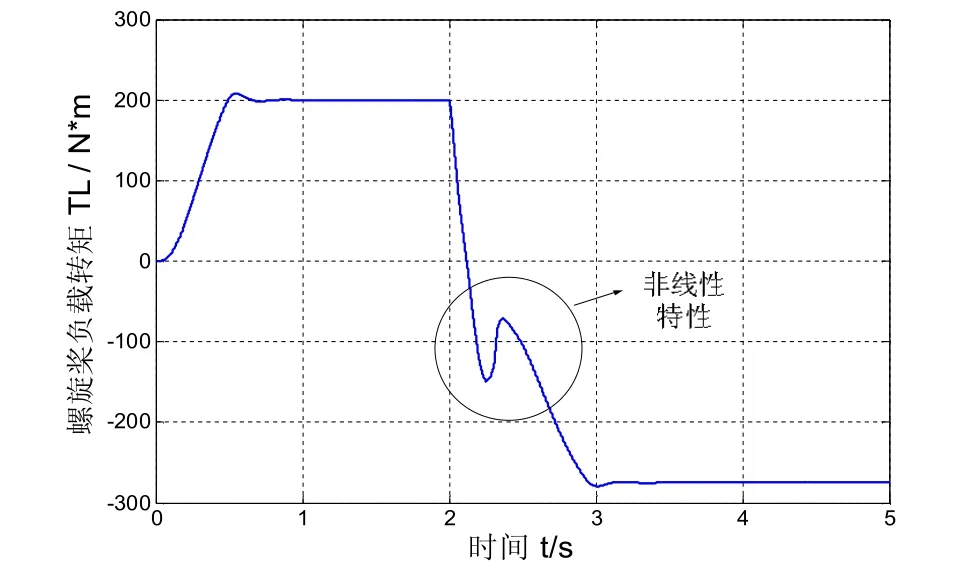
图7 螺旋桨负载转矩

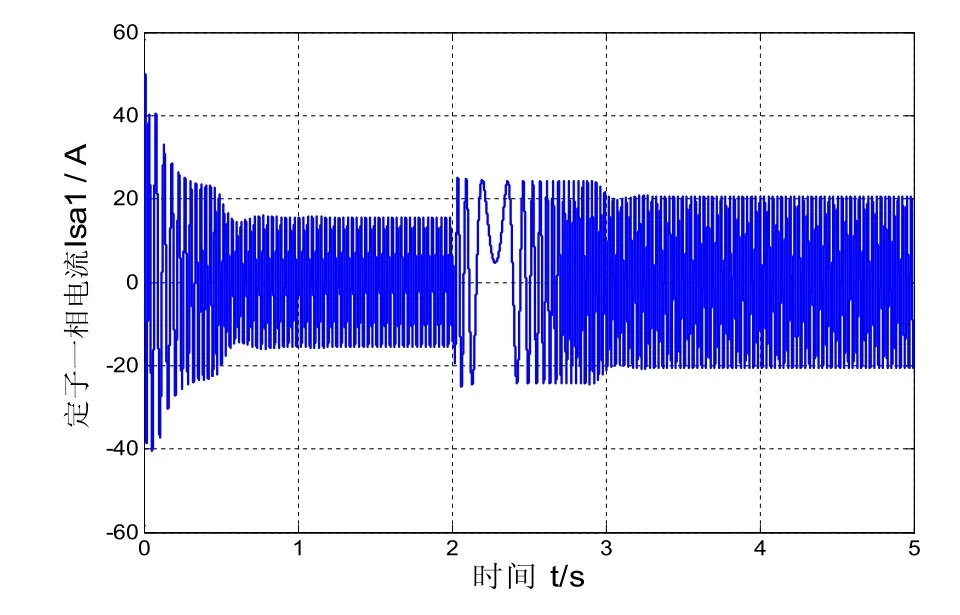
图8 十五相电机定子一相的电流

5 结论

本文分析了十五相电机的数学模型，并建立了其仿真模型；利用插值查表，建立了能够反应非线性负载特性的螺旋桨仿真模型。通过研究十五维解耦矩阵及其物理意义，建立了十五相感应电机在广义派克变换下的数学模型，由此推导了转子磁场定向矢量控制。将全系统在MATLAB/Simulink中建模，通过自由航行和紧急倒车两种工况下的仿真，验证了仿真模型的合理性，也验证了矢量控制策略的正确性和有效性。

本研究完全基于仿真实验，更具有实际意义的研究还有待后期物理实验的进行。

[1]Ådnanes,A.K.Maritime electrical installations and diesel electric propulsion.Tutorial Report/Textbook[M],ABB Marine AS,Oslo,Norway,2003.

[2]Apsley,J.M.,Gonzalez-Villasenor,A.,Barnes,M.,et al.Propulsion drive models for full electric marine propulsion systems[J],IEEE Transactions on Industry Applications,2009,45(2): 676-684.

[3]Levi,E.,Bojoi,R.,Profumo,F.,et al.Multiphase induction motor drives-a technology status review[J],Electric Power Applications,IET,2007,1(4):489-516.

[4]Levi,E.Multiphase electric machines for variable-speed applications[J],IEEE Transactions on Industrial Electronics,2008,55(5): 1893-1909.

[5]薛山.多相永磁同步电机驱动技术研究[D].中国科学院研究生院（电工研究所）,2006.

[6]欧阳红林.多相永磁同步电动机调速系统控制方法的研究[D].湖南大学,2005.

[7]Carrasco,G.and Silva,C.A.space vector PWM method for five-phase two-level VSI with minimum harmonic injection in the overmodulation region[J],IEEE Transactions on Industrial Electronics,2013,60(5): 2042-2053.

[8]Jones,M.,Satiawan,I.N.W.,Bodo,N.,et all.A dual five-phase space-vector modulation algorithm based on the decomposition method[J],IEEE Transactions on Industry Applications,2012,48(6): 2110-2120.

[9]吴新振,王祥珩,罗成.多相异步电机谐波电流与谐波磁势的对应关系[J].清华大学学报(自然科学版),2005,45(7): 865-868.

[10]李殿璞.船舶运动与建模[M].北京: 国防工业出版社,2008.

[11]李永东.交流电机数字控制系统（第二版）[M].北京: 机械工业出版社,2012.

[12]王又珑.十五相感应电机磁场分析及驱动技术研究[D].中国科学院研究生院（电工研究所）,2009.