基于作物缺水指数的土壤含水量估算方法
虞文丹,张友静,2,郑淑倩
(1.河海大学地球科学与工程学院,南京 210098;2.河海大学水文水资源与水利工程科学国家重点实验室,南京 210098;3.浙江华东测绘有限公司,杭州 310030)
0 引言
鉴于传统干旱监测的局限性和遥感技术的宏观、动态、客观、时效性等特点,利用遥感技术进行干旱监测已成为当前的研究热点[1]。遥感监测干旱的方法有热惯量法、冠层温度法、植被指数法、作物缺水指数法和微波遥感法等。其中,作物缺水指数法以能量平衡为基础,物理意义明确,适用范围广,在植被覆盖度较大的地区,估算精度高于热惯量法。袁国富等[2]对国内外基于冠层温度的作物缺水指标进行了总结。Jackson等[3-4]利用土壤水分和农田蒸散来诊断作物水分胁迫状况,并在植被覆盖条件下取得了较高的监测精度。申广荣等[5]建立单层作物缺水指数(crop water stress index,CWSI)模型来监测黄淮海平原旱情,基本实现了准确、实时监测。获取CWSI的关键在于实际蒸散发量的计算,王纯枝等[6]对潜在蒸散量计算和CWSI法干旱遥感监测模型进行了简化,实现对土壤水分的定量反演,简化后的CWSI法充分考虑到下垫面植被覆盖信息和气象要素状况,能够准确反演土壤缺水状况。宋小宁等[7]利用MODIS数据,通过建立基于亚像元尺度的双层蒸散模型,在CWSI基础上利用地表缺水指数进行了非均质下垫面区域缺水监测,但其研究范围局限于西北半干旱草原区。刘振华等[8]在植被覆盖区,利用半干旱地区基于亚像元的土壤蒸发和植物蒸腾双层模型,剥离土壤的影响,获取缺水指数模型中的植被潜热通量,并利用遗传算法对该区进行混合像元分解,获取模型中的地表组分温度参量,但其采用的ASTER数据分辨率较低,样点较少,反演精度受到一定影响。
本文以2010年江苏省徐州市为研究区域,以MODIS数据为主要数据源,结合地面实测数据和气象数据,运用蒸散发双层遥感模型,建立作物缺水指数模型,估算20 cm土层土壤相对含水量。在蒸散发模型中,考虑土壤水分可供率对显热通量的影响,改进了原模型。
1 研究区概况与数据源
徐州市位于江苏省的西北部,介于E116°22'~118°40',N33°43'~ 34°58'之间,暖温带季风气候,四季分明,雨热同期,年均气温14°C。土地总面积11 258 km2,是我国重要的粮食产区。近几十年来,干旱成为徐州市主要的气象灾害,一般年缺水量约30×108m3,干旱年份缺水量高达80×108m3。研究区概况见图1。
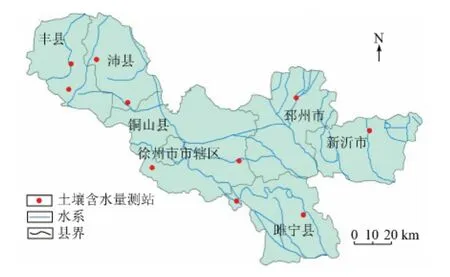
图1 研究区概况Fig.1 General situation of research area
研究区数据主要包括5个方面:①研究区矢量边界、气象站空间位置坐标以及水文专题数据层等基础地理信息数据;②用于反映地表温度、地表植被覆盖情况以及地表比辐射率等信息的MODIS影像数据,包括陆地3级标准数据产品,2010年日尺度、8 d尺度、16 d尺度的产品影像数据;③气温、风速及降水等地面气象站观测数据;④20 cm土层土壤相对含水量的农业气象观测数据;⑤用于地形修正的DEM数字高程模型。所有影像数据都统一到同一投影系统下,并重采样到1 000 m。对于基于点尺度的气象数据,采用克里金法插值到像元尺度。
2 研究方法
2.1 作物缺水指数模型
土壤含水量对蒸散速率有一定影响。Jackson等[9]以能量平衡为基础,利用热红外遥感温度和气象资料,间接监测植被覆盖条件下的土壤水分,提出了CWSI的概念,即
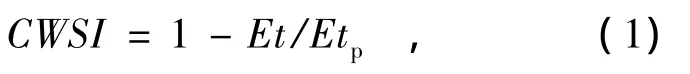
式中:Et为实际蒸散发量,mm;Etp为潜在蒸散发量,根据 Penman-Monteith公式[10]计算得到,mm。
CWSI的实质是反映植被蒸腾与最大可能蒸发的比值,由作物冠层温度值转化而来,可在一定程度上反映植物根系范围内土壤水分的信息,用来度量作物缺水程度。由式(1)可知,获取CWSI的关键在于实际蒸散发量的计算。本文通过构建土壤表层含水量W与作物缺水指数CWSI之间的关系来对土壤含水量进行模拟,即

2.2 实际蒸散发量的估算
2.2.1 双层蒸散发模型
双层模型的理论基础为能量平衡方程,简化的能量平衡原理的方程满足
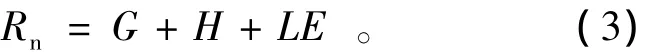
式中:Rn为地表净辐射通量,是地表所接收到的能量总和,W·m-2;G为下垫面地表的土壤热通量,表明土壤表层和深层热量传递的情况,用于下垫面地表升温,W·m-2;H为地表与空气间进行热交换的部分能量,称为感热通量或显热通量,W·m-2;LE为潜热通量,为地表与大气间水汽热交换的定量描述,W·m-2,其中L为单位质量的水汽化过程中所吸收的热量,俗称水的汽化潜热,W·m-2,E为瞬时蒸散量,mm。
由于双层模型明确了冠层和土壤2个界层的能量交换、传输和平衡关系,能从蒸散过程原动力—能量角度揭示蒸散机理,因而提高了模拟精度。双层模型的基本思想是:水汽和热量的2个源是互相叠加的,底层的水与热量只能通过顶层离开或进入,从整个冠层散发的总显热通量是各层显热通量之和。双层模型分离土壤和植被,利用遥感反演的地表特征参数,结合必要的气象参数,分别考虑地表平衡方程中各地表通量,并建立各自的植被冠层和土壤大气界面处的能量平衡方程[11-14],即
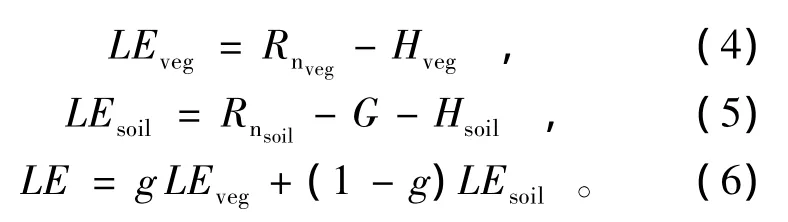
式中:下标veg,soil分别表示各通量在植被层和土壤层的分量大小;g为下垫面植被覆盖度。地表净辐射通量Rn的计算公式为
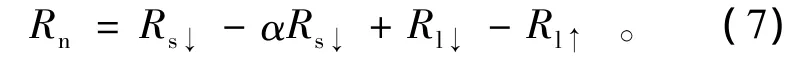
式中:Rs↓,αRs↓分别表示入射短波辐射以及地表反射短波辐射,W·m-2,其中 α 为地表反照率;Rl↓,Rl↑为入射长波辐射以及地表向大气发射的长波辐射,W·m-2。通常,Rs↓除受到影像获取时刻太阳辐射强度的影响外,相应的大气条件,如云量、湿度、空气清洁度以及大气厚度等对到达地面的太阳辐射能量具有一定的削减作用。综合考虑以上因素,在晴空无云的状况下,Rs↓的计算过程为

式中:Gsc为太阳常数,通常取1 367W·m-2;dr为日地相对距离;τsw为单向透过率;z为地面高程;θ为太阳天顶角;D为数据获取日在一年中的顺序天数。
地表入射长波辐射R1↓和R1↑出射长波辐射根据stefarr-boltzmann定律计算,即

式中:εs,εa分别为地表比辐射率和空气比辐射率,前者采用产品数据,后者可通过气温和实际水汽压计算得到;Ts,Ta分别为地表温度和空气温度,K,前者采用产品数据,后者可通过对气象站点的观测数据克里金插值得到;σ为玻尔兹曼常数,通常取5.67 ×10-8W·m-2·K-4。
在双层模型中,土壤组分和植被组分各自独立地与外界空气进行湍流交换,即

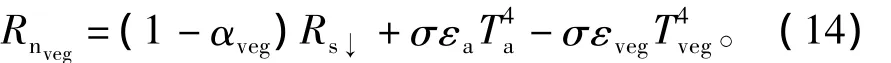
式中:εsoil为裸土地表比辐射率,通常取0.93;εveg为全植被覆盖情况下的地表比辐射率,通常取0.993;αveg,αsoil为地表组分反照率;Tveg,Tsoil分别为植被和土壤组分温度。
混合像元的净辐射通量Rn则可通过组分净辐射通量关于植被覆盖度加权计算得到,即
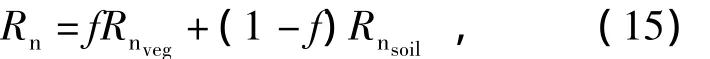
式中f为权值。土壤热通量与净辐射通量的比值是关于植被覆盖度、地表温度以及地表反照率的非线性函数。本文综合考虑这些因子,采用
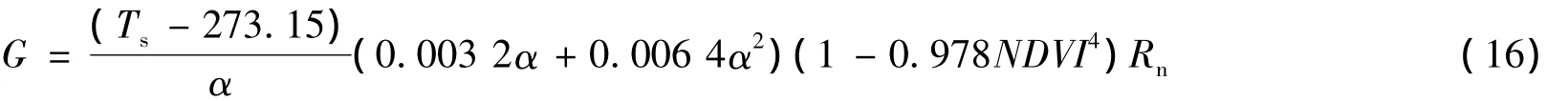
进行土壤热通量G的估算。式中NDVI为归一化植被指数。通常,G白天为正,夜晚为负,一般在计算日尺度土壤热通量时可近似为0。
双层模型深入到亚像元级别,认为复杂下垫面主要由植被层和土壤层组成,各层显热通量的计算方式有所差异。在密集植被区,地表温度(Ts)与空气动力学温度(T0)近似相等,因此在计算植被组分显热通量时可直接采用植被组分温度(Tveg)代替T0。而在土壤层,土壤组分温度(Tsoil)与T0间温差较大,若采用Tsoil直接代替T0,则需引入“剩余阻抗”以修正观测角度和风速等对辐射温度的影响。综上,各组分显热通量(Hveg,Hsoil)的计算方法为

式中:ρ为空气密度,kg·m-3,可根据气温和高程计算得到;Cp为空气定压比热常量,通常取值1 004 J·kg-1·℃-1;Ta为参考高度(2 m)处的空气温度,K;ra为空气动力学阻抗,s·m-1;rbh为剩余阻抗,s·m-1。
双层蒸散发模型计算的蒸散发数据为瞬时蒸散发,利用谢贤群[15]正弦曲线法将其拓展到日尺度。
2.2.2 地表参数的反演
2.2.2.1 地表组分温度

图2 植被覆盖度g与地表温度T s梯形空间Fig.2 Trapezoidal space of g and T s
本文参考了像元排序对比法(pixel component arranging and comparing algorithm,PCACA)法的理论基础对地表组分温度进行计算,并对其加以改进。首先,假设土壤和植被冠层的耦合机制符合双层模型的平行模式,单株植被与贴近的土壤构成了双层模型的最小单元,两者的辐射源和驱动力可以有所区别,土壤表面温度和植被冠层温度也不一样,但是由于植被根系的扩展和土壤水分的侧渗作用,在最小单元内,植被和土壤的水分供应状况视为相同。因此,干边和湿边间存在的过渡等土壤湿度线与等斜率线一致。如图2所示,在大部分情况下,研究区内并不存在所有条件的点。通过散点拟合方法得到的干湿边(③④分别表示相对干边和相对湿边)并不能完全等同于绝对意义上的极端情况。本文绝对干边定义为地表含水量接近凋萎系数,水分胁迫作用显著,蒸散量几乎为0;绝对湿边定义为发生在地表充分供水的情况下,实际蒸散发接近潜在蒸散发。可通过搜索干裸地(P1)、干全植被覆盖地(P2)、湿裸地(P3)及湿全植被覆盖地(P4)来确定绝对干湿边的线性方程,进而得到“覆盖度-地表温度”的梯形结构。P1,P2,P3和P4对应到纵坐标上的值为Tsd,Tvd,Tsw和Tvw,分别表示干裸地的地表温度、干全植被覆盖地的地表温度及湿裸地的地表温度和湿全植被覆盖地的地表温度。Tsmin,Tsmax分别表示特征空间的湿边和干边在某植被盖度下的温度取值,即相应植被覆盖度下的最小温度和最大温度。
当土壤相当干燥时,地表含水量接近凋萎含水量,此时已经不存在土壤蒸发及植被蒸腾作用,地表所接收的净辐射通量完全用于加热近地表大气H以及土壤内部的热量交换G,能量平衡方程可简化为

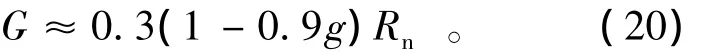
对于干裸地,植被覆盖度g=0,其能量平衡方程满足
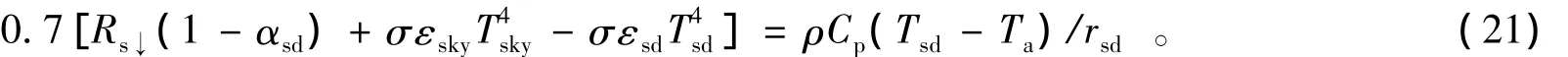
干裸地的地表温度可以表示为
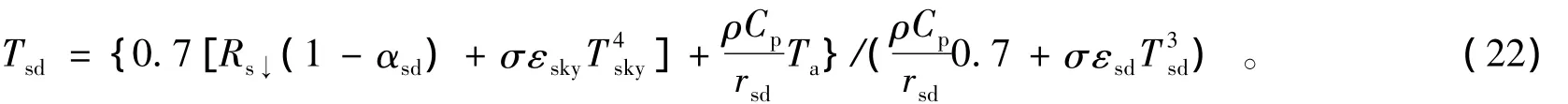
式中:Tsd为干裸地的地表温度;αsd为干裸地的地表反照率;εsky和εsd分别为空气和干裸地的地表比辐射率;rsd为干裸地所受的阻抗,包括空气动力学阻抗以及剩余阻抗;Tsky为像元上空天穹的平均温度,可利用水汽压ea和空气温度Ta计算得到,即
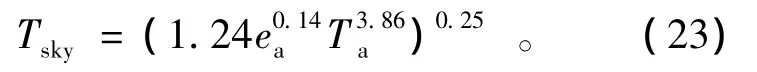
考虑到天空等效温度T4sky及风速的单点地面观测值具有一定的局地代表性,因此气象参数采用研究区内最干裸地对应的像元值。Tsd,αsd是计算绝对干裸地地表温度的关键参数,鉴于“植被覆盖度-地表温度”“地表反照率-地表温度”均满足梯形结构,拟采用散点拟合干边在植被覆盖度为0处的取值作为Tsd,αsd的输入。根据式(22)计算出Tsd,从而得到梯形4个特征点中P1的解。延着上述思路,当地表处于完全植被覆盖时,反照率、空气动力学阻力及植被冠层表面温度会发生较明显的变化。完全植被覆盖点的冠层表面温度Tvd满足

式中:Tvd为干全植被覆盖地的地表温度;αvd为干全植被覆盖地的地表反照率;εvd为干全植被覆盖地的地表比辐射率;rvd为干全植被覆盖地所受的阻抗,包括空气动力学阻抗以及剩余阻抗。气象参数仍可通过研究区内最高植被覆盖度地所在像元值获取。此时下层土壤达到凋萎含水量,植被受到较严重的水分胁迫作用。
2.2.2.2 地表组分反照率
就研究区而言,红外波段的每个像元热辐射能Li是由地表植被和土壤共同作用的结果,即

2.2.2.3 剩余阻抗
剩余阻抗是风速等参数对辐射温度影响的经验值,其实质是引入无量纲参数KB-1,以获取动量粗糙度长度和热量粗糙度长度之间的转换,即
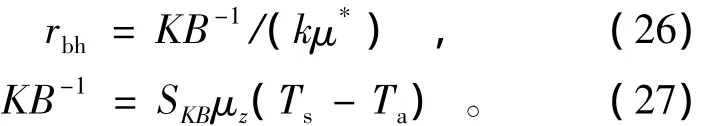
式中:SKB为经验系数,有效值范围在0.05~0.25之间;k为von Karman常数,通常取0.41;μ*为摩阻速度;μz为参考高度z处的风速。
2.2.3 改进双层蒸散发模型
在原有的双层模型基础上引入土壤水分可供率参数,可增强模型对地表湿度变化的敏感性。目前,大多数能量平衡模型并没有明确地指出土壤湿度与蒸散发间的关系,而是在计算显热通量时以地表温度来反映地表供水状况。当太阳热辐射成为抑制蒸散作用的重要因子时,上述假设是成立的。当下垫面干燥、太阳辐射强度较大的情况下,应用上述模型估算的日蒸散发往往较实际值高 1.5 ~3.0 mm[16],主要原因是由显热通量计算值偏小导致的。Gokmen M[17]利用站点的土壤湿度观测值改进了SEBS模型中参数KB-1的计算方法,显热通量的估算精度有了明显的提高。
本文在原有的双层模型基础上引入土壤水分可供率参数,增强模型对地表湿度变化的敏感性。土壤水分可供率是实际蒸散发耗水量的定量描述,可通过温度植被干旱指数(temperature vegetation dryness index,TVDI)计算得到,有效地解决了空间尺度不一致的问题,即
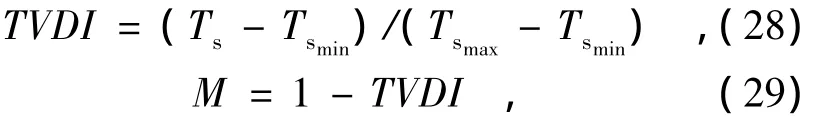
式中M为土壤水分可供率。
在显热通量的计算中引入剩余阻抗项,采用土壤水分可供率对剩余阻抗的经验公式进行改进,采用式(31)拟合剩余阻抗的修正因子[17],即
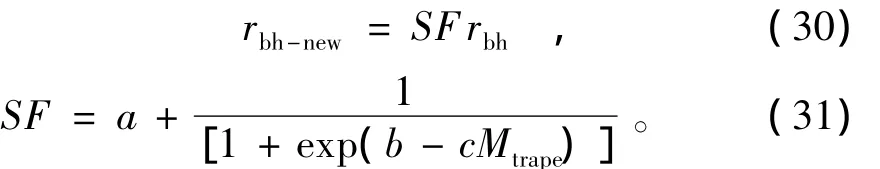
式中:rbh-new为改进后的剩余阻抗;SF为剩余阻抗的修正因子;Mtrape为基于温度植被干旱指数法估算得到的土壤水分可供率;a,b,c为系数。
将修正后的剩余阻抗引入到双层模型中,计算区域瞬时蒸散发数据,利用谢贤群正弦曲线法将其拓展到日尺度后取平均得到月平均蒸散发值,分布图如图3。从中可以看出,区域整体蒸散发分布为西面蒸散发较低,东面蒸散发较高;7月份区域蒸散发高于11月份。
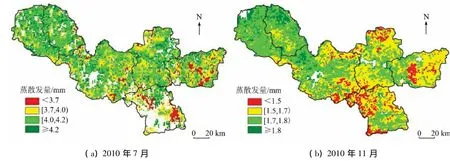
图3 基于改进双层模型的月平均蒸散发量分布图Fig.3 Map of monthly average evapotranspiration based on improved double layer model
2.3 土壤相对含水量估算模型构建
2.3.1 基于双层蒸散发模型
利用式(1)计算基于双层蒸散发模型的CWSI,利用式(2)构建基于CWSI的土壤相对含水量模型。得到实测的各观测站点20 cm土层土壤相对含水量值与计算出的CWSI值构建的散点图(图4)。

图4 土壤相对含水量实测值与CWSI关系图Fig.4 Diagram of CWSI and measured values of the relative content of water
从图4看出,土壤相对含水量与CWSI呈反比关系,CWSI值越小,土壤表层水分含量越大。拟合的相关系数分别为0.53和0.72。7月份作物播种及农田灌溉影响了部分站点模型的拟合精度。
2.3.2 基于改进双层蒸散发模型
利用公式(1)计算基于改进双层蒸散发模型的CWSI,得到区域7月和11月的月平均CWSI,如图5所示。

图5 基于改进双层模型的月平均CWSI分布图Fig.5 Map of monthly average CWSI based on improved double layer model
从图5看出,区域CWSI分布为西低东高。根据土壤相对含水量与CWSI之间的关系反演土壤水分。反演结果表明,7月份和11月份实测值与估算值的决定系数都为0.84,平均相对误差分别为3.47%和6.03%,拟合精度明显高于改进前模型的拟合精度,拟合直线斜率为1,截距为0,模型没有系统误差。具体关系图见图6。
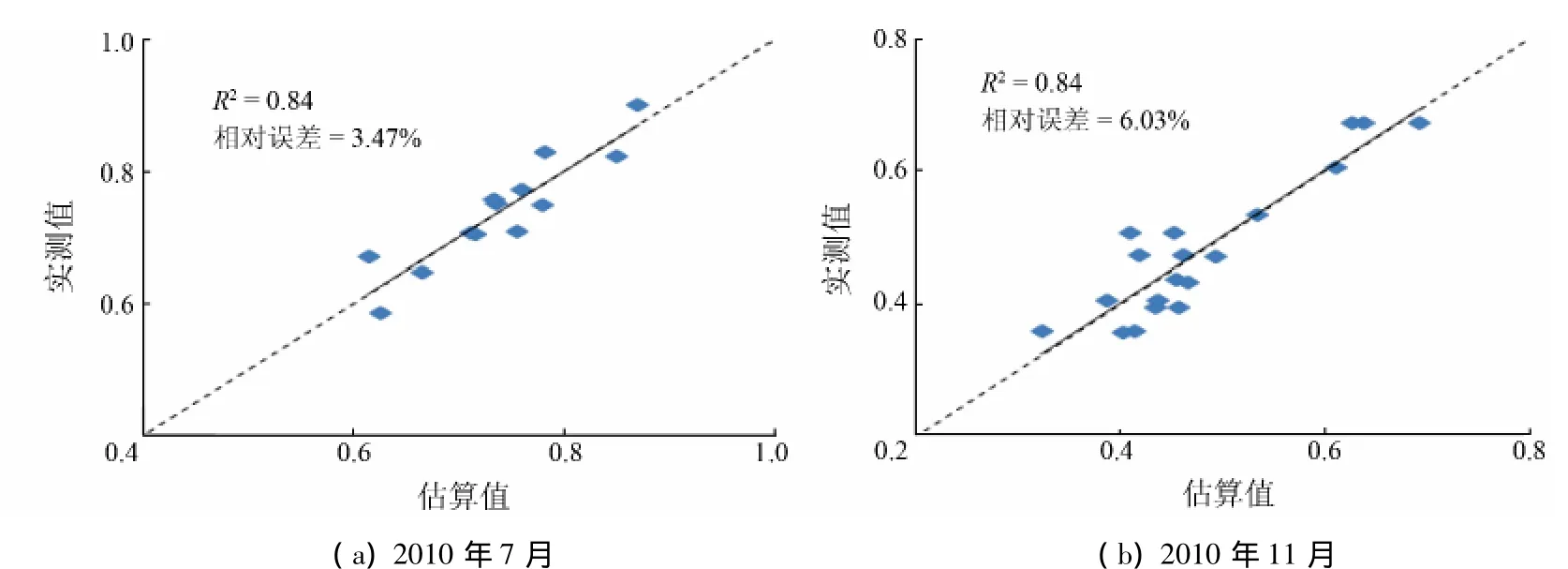
图6 土壤相对含水量估算值与实测值关系图Fig.6 Diagram of estimated values and measured values of the relative content of water
绘制徐州市2010年7月与11月20 cm土层月 平均土壤相对含水量反演图,如图7所示。
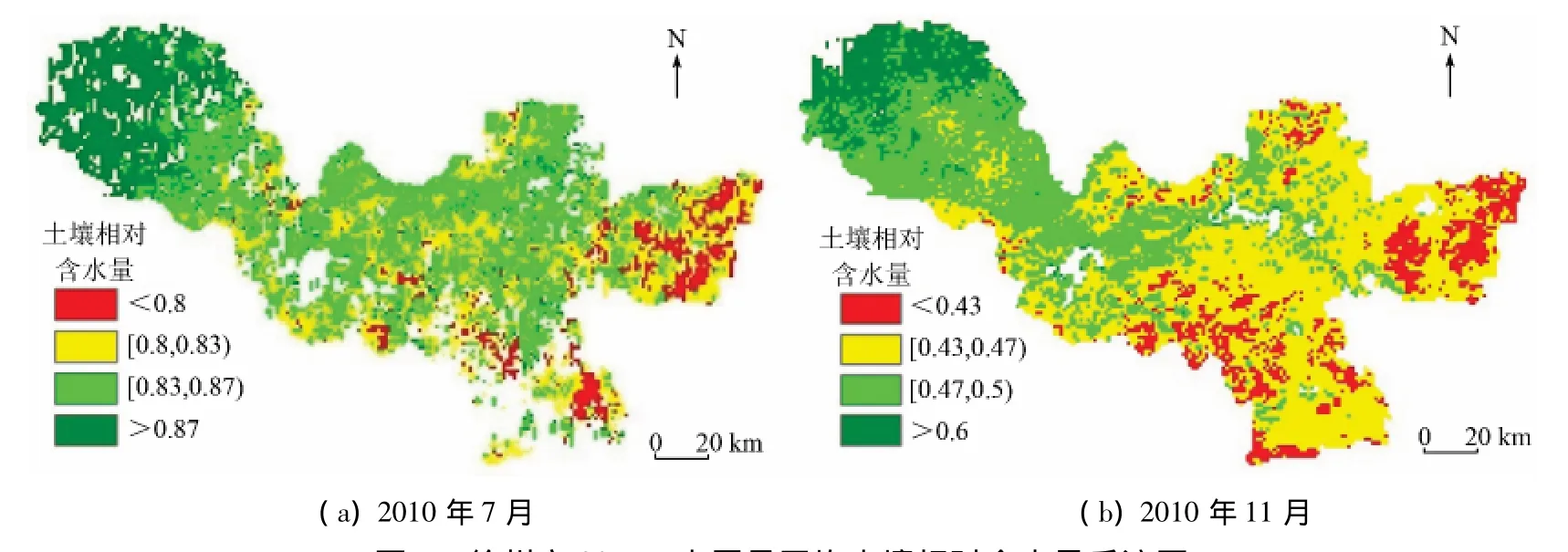
图7 徐州市20 cm土层月平均土壤相对含水量反演图Fig.7 Inversed maps of the monthly average relative content of water with 20 cm depth soil in Xuzhou City
由图7可以看出,徐州市土壤含水量空间变化为西高东低,时间上受降雨影响7月份土壤含水量高于11月份。
3 结论
本文主要从能量平衡角度出发,利用土壤水分可供率对双层模型剩余阻抗进行修正,计算改进后实际蒸散发量,构建日作物缺水指数,建立了作物缺水指数与土壤水分含量之间的经验关系式,进而估算空间大范围区域的土壤水分含量。
1)利用改进后的实际蒸散发估算土壤表层含水率的精度高于改进前,2010年7月份与11月份的相对误差分别为3.47%和6.03%。
2)大多数能量平衡模型并没有明确地指出土壤湿度与蒸散发间的关系,改进后的双层模型考虑了下垫面湿度的影响,意在解决下垫面干燥、太阳辐射强度较大的情况下,显热通量计算值偏小的问题,也更具有物理意义。
3)土壤含水量的准确监测依赖于遥感参数定量反演的精度和数据在时间尺度、空间尺度上的匹配,这也成为下一步的努力方向。
[1] 冯蜀青,殷青军,肖建设,等.基于温度植被旱情指数的青海高寒区干旱遥感动态监测研究[J].干旱地区农业研究,2006,24(5):141-145.Feng SQ,Yin Q J,Xiao JS,et al.Monitoring drought dynamic variation based on temperature vegetation drought index in Qinghai high and cold area[J].Agricultural Research in the Arid Areas,2006,24(5):141-145.
[2] 袁国富,唐登银,罗 毅,等.基于冠层温度的作物缺水研究进展[J].地球科学进展,2000,16(1):49-54.Yuan G F,Tang D Y,Luo Y,et al.Advances incanopy-temperature based crop water stress research[J].Advances in Earth Science,2000,16(1):49-54.
[3] Jackson R D,Idso SB,Reginato R J,et al.Canopy temperature as a crop water stress indicator[J].Water Resources Research,1981,17(4):1133-1138.
[4] Zhang RH.A newmodel for estimating crop water stress based on infrared radiation information[J].Science in China B,1986,7:776-784.
[5] 申广荣,田国良.作物缺水指数监测旱情方法研究[J].干旱地区农业研究,1998,16(1):123-128.Shen GR,Tian G L.Drought monitoring with crop water stress index[J].Agricultural Research in the Arid Areas,1998,16(1):123-128.
[6] 王纯枝,毛留喜,吕厚荃,等.基于作物缺水指数的区域旱情遥感监测[C]//中国气象学会2007年年会生态气象业务建设与农业气象灾害预警分会场论文集.北京:中国气象学会,2007.Wang C Z,Mao L X,Lv H Q,etal.Monitor regional drought based on crop water stress index[C]//Meteorological Service Construction and Agricultural Meteorological Disaster Warning Breakout of China Meteorological Society in 2007.Beijing:China Meteorological Society,2007.
[7] 宋小宁,赵英时.改进的区域缺水遥感监测方法[J].中国科学(D 辑:地球科学),2006,36(2):188-194.Song X N,Zhao Y S.Improved regional drought test method[J].Science in China(Ser D:Earth Sciences),2006,36(2):188-194.
[8] 刘振华,赵英时,李笑宇,等.基于蒸散发模型的定量遥感缺水指数[J].农业工程学报,2012,28(2):114-120.Liu Z H,Zhao Y S,Li X Y,et al.Quantitative remote sensing of water deficit index based on evapotranspiration[J].Transactions of the CSAE,2012,28(2):114-120.
[9] Jackson T J,Le Vine D M,Hsu A Y,et al.Soil moisture mapping at regional scales usingmicro wave radiometry:The Southern Great Plains Hydrology Experiment[J].IEEE Transactions on Geoscience and Remote Sensing,1999,37(5):2136-2151.
[10] 刘 钰,Pereira L S,Teixeira J L,等.参照腾发量的新定义及计算方法对比[J].水利学报,1997(6):27-33.Liu Y,Pereira L S,Teixeira JL,et al.Update definition and computation of reference evapotranspiration comparison with former method[J].Journal of Hydraulic Engineering,1997(6):27-33.
[11] 辛晓洲,田国良,柳钦火.地表蒸散定量遥感的研究进展[J].遥感学报,2003,7(3):233-240.Xin X Z,Tian G L,Liu Q H.A review of researches on remote sensing of land surface evapotranspiration[J].Journal of Remote Sensing,2003,7(3):233-240.
[12] James Shuttle worth W,Gurney R J.The theoretical relationship between foliage temperature and canopy resistance in sparse crops[J].Quarterly Journal of the Royal Meteorological Society,1990,116(492):497-519.
[13] Norman JM,KustasW P,Humes K S.Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature[J].Agricultural and Forest Meteorology,1995,77(3):263-293.
[14] 张仁华,孙晓敏,王伟民,等.一种可操作的区域尺度地表通量定量遥感二层模型的物理基础[J].中国科学(D辑:地球科学),2004,34(s2):200-216.Zhang R H,Sun X M,Wang W M,et al.An operational regional scale surface fluxes of quantitative remote sensing model of two layers ofbasic physics[J].Science in China(Ser D:Earth Sciences),2004,34(s2):200-216.
[15] 谢贤群.遥感瞬时作物表面温度估算农田全日蒸散总量[J].环境遥感,1991,6(4):253-260.Xie X Q.Estimation of daily evapo-transpiration(ET)from one time-of-day remotely sensed canopy temperature[J].Remote Sensing of Environment China,1991,6(4):253-260.
[16] Lubczynski M W,Gurwin J.Integration of various data sources for transient groundwater modeling with spatio-temporally variable fluxes-Sardon study case,Spain[J].Journal of Hydrology,2005,306(1/4):71-96.
[17] Gokmen M,Vekerdy Z,Verhoef A,etal.Integration of soil moisture in SEBS for improving evapotranspiration estimation under water stress conditions[J].Remote Sensing of Environment,2012,121:261-274.

