转向梯形双间隙对汽车蛇行工况稳定性的影响

魏道高张志龙蒋统潘之杰肖怀阳

（1.合肥工业大学；2.浙江吉利汽车研究院有限公司）

转向梯形双间隙对汽车蛇行工况稳定性的影响

魏道高1张志龙1蒋统1潘之杰2肖怀阳2

（1.合肥工业大学；2.浙江吉利汽车研究院有限公司）

将转向梯形简化为平面连杆机构，建立包含车身侧倾、横摆、侧偏及右前轮转角的4自由度车辆转向行驶系统数学模型，并采用数值方法对转向梯形运动副双间隙参数变化时样车质心侧偏角的稳定性进行计算分析。结果表明，随着运动副间隙增大，汽车蛇形运动的单周期区域减小，倍周期区域消失，混沌区域增加；理论上找到间隙r＜1.0 mm区间时汽车蛇形工况失稳区间较小。

1 前言

汽车转向梯形间隙对汽车行驶稳定性有重要影响。目前的文献多是针对转向梯形间隙对汽车摆振工况的研究，如卢剑伟[1]在摆振模型中考虑转向梯形轴销间隙，对含2状态间隙模型分析发现，间隙可能导致汽车摆振动力学行为出现倍周期并最终走向混沌；王威[2]以4DOF独立悬架汽车为研究对象，运用频域分析方法研究发现，转向梯形间隙可以改善系统的瞬态响应行为。而关于转向梯形间隙对于汽车操纵稳定性能如汽车蛇形工况影响的研究则较少。

由于生产制造和装配误差及日常使用磨损等不可控因素，转向梯形间隙难以避免。研究转向梯形间隙对汽车蛇形工况稳定性的影响，可以确定间隙的合理误差范围，使其既满足生产制造易于实现又能保证汽车日常行驶安全。本文在以上研究成果及前期研究单间隙对汽车转向行驶稳定性影响[3]的基础上，进一步考虑转向梯形双间隙对车辆蛇形工况稳定性的影响，建立了含车身侧倾运动的4DOF汽车转向行驶非线性动力学模型，并进行了数值计算与分析，以获得间隙因素对汽车蛇行工况下频率特性的影响。

2 含双间隙的转向梯形转向行驶模型

2.1 考虑双间隙的系统力学模型

在前期建立的汽车转向行驶系统力学模型基础上，考虑转向机构双间隙对转向稳定性的影响，建立样车转向系统力学模型和坐标系如图1所示。

建模时考虑转向横拉杆球头销处双间隙，为了简化分析过程，忽略前轮定位参数及转向梯形杆件的空间夹角对汽车转向运动的影响，则汽车整体式转向梯形简化为平面四连杆机构[4]，如图1c所示。汽车以速度V做匀速蛇行行驶，OXYZ为固定于侧倾中心的坐标系，XOY与路面平行，X轴指向汽车行驶方向，Z轴竖直向上，Y轴按右手定则指向左侧。

汽车转向行驶系统用横摆角速度ω、质心侧偏角β、车身侧倾角φ和右前轮转向角δr共4个自由度表示。

2.2 含双间隙汽车转向行驶运动方程

根据以上车辆转向行驶力学模型，运用达朗贝尔定理，建立车辆转向行驶整车运动微分方程。

2.2.1 车辆转向行驶运动方程

整车绕Z轴力矩平衡方程：

整车沿Y轴力平衡方程：

车身绕X轴侧倾力矩平衡方程：

前从动轮（右）绕主销的力矩平衡方程：

式中，Fyfl为左前轮侧偏力；Fyfr为右前轮侧偏力；Fyrl为左后轮侧偏力；Fyrr为右后轮侧偏力；δr为右前轮转角；δl为左前轮转角；lf为前轴距；lr为后轴距；m为整车质量；ms为簧上质量；hs为簧上质量质心到侧倾轴线距离；Ix为簧上质量绕x轴转动惯量；Ixz为簧上质量绕x、z两轴惯性积；Iz为整车绕z轴转动惯量；cφ为车身侧倾角阻尼；kφ为车身侧倾角刚度；Jc为右梯形臂绕右侧主销的转动惯量；Dw为回正力臂；Mp为间隙对主销碰撞力矩；为右梯形臂的转动角加速度。

a.轮胎侧向力表达式

汽车轮胎侧向力选用简化的魔术公式[14]：

式中，B、C、D和E分别对应为侧向力魔术公式中的刚度因子、形状因子、峰值因子和曲率因子；a1、a2、a3、a4、a5、a6、a7和a8为根据样车厂家提供的轮胎侧向力试验数据结合魔术公式利用Matlab软件进行拟合得到的参数；Fz为轮胎所受载荷；α为轮胎侧偏角。

由轮胎侧向力表达式和表1的轮胎魔术公式参数可得样车轮胎侧向力Fy与侧偏角α的关系如图2所示。

表1 轮胎魔术公式参数

b.前后轮的侧偏角表达式

c.车辆转向行驶时左右车轮载荷转移表达式

前桥左轮载荷：

前桥右轮载荷：

后桥左轮载荷：

后桥右轮载荷：

式中，Kφf为前悬架侧倾角刚度；Kφr为后悬架侧倾角刚度；Cφf为前悬架侧倾角阻尼；Cφr为后悬架侧倾角阻尼；d为轮距；muf为前轴簧下质量；mur为后轴簧下质量；hf为前侧倾中心到地面距离；hr为后侧倾中心到地面距离；huf为前轴簧下质量到地面距离；hur为后轴簧下质量到地面距离；lfs为簧上质量前轴距；lrs为簧上质量后轴距。

2.2.2 双间隙转向梯形机构碰撞力矩求解

根据图1c车辆转向行驶时转向梯形机构简化力学模型，求解右球头间隙碰撞力矩。在图1c中，右球头间隙碰撞模型选用2状态间隙碰撞模型，设左、右轴销中心和轴套中心之间的距离为ei，ei，沿X、Y轴的分量分别为eix、eiy（i=1，2），由其几何关系可得：

设接触角φi由下式表示：

设间隙中轴销相对于轴套的法向速度和切向速度分别为vin和vit：

间隙运动副碰撞力中法向力Pin与切向力Pit分别为：

式中，K为间隙处轴套表面刚度；f为间隙处轴套表面摩擦系数；r为间隙；Cn为间隙处轴套表面法向阻尼系数；Ct为间隙处轴套表面切向阻尼系数。

其中，

则右轴销碰撞力在X、Y方向的分量为：

式中，R为轴销半径；左前轮转角输入为

由此可得间隙对主销的碰撞力矩为：其中，A为左前轮转动幅值；f为左前轮转动角频率。

3 汽车蛇行工况下频率特性计算与分析

以某型国产轿车为样车，计算时所需样车参数见表2，根据前述数学模型，利用数值方法分析转向梯形双间隙对汽车蛇形工况稳定性的影响。

3.1 转向机构及其间隙对汽车蛇行频率特性影响

根据表2中样车参数，对其转向梯形机构（图1c）中球头间隙r分别取0、0.5 mm、1 mm、1.5 mm、2 mm进行数值计算，寻找间隙对车辆蛇行工况频率特性的影响规律。图3为当左轮转角幅值A取0.15 rad，间隙r分别取0、0.5 mm、1.0 mm、1.5 mm、2.0 mm时，车辆蛇行工况质心侧偏角频率特性分叉图。表3为不同间隙车辆失稳时质心侧偏角的上、下失稳临界频率及失稳带宽。

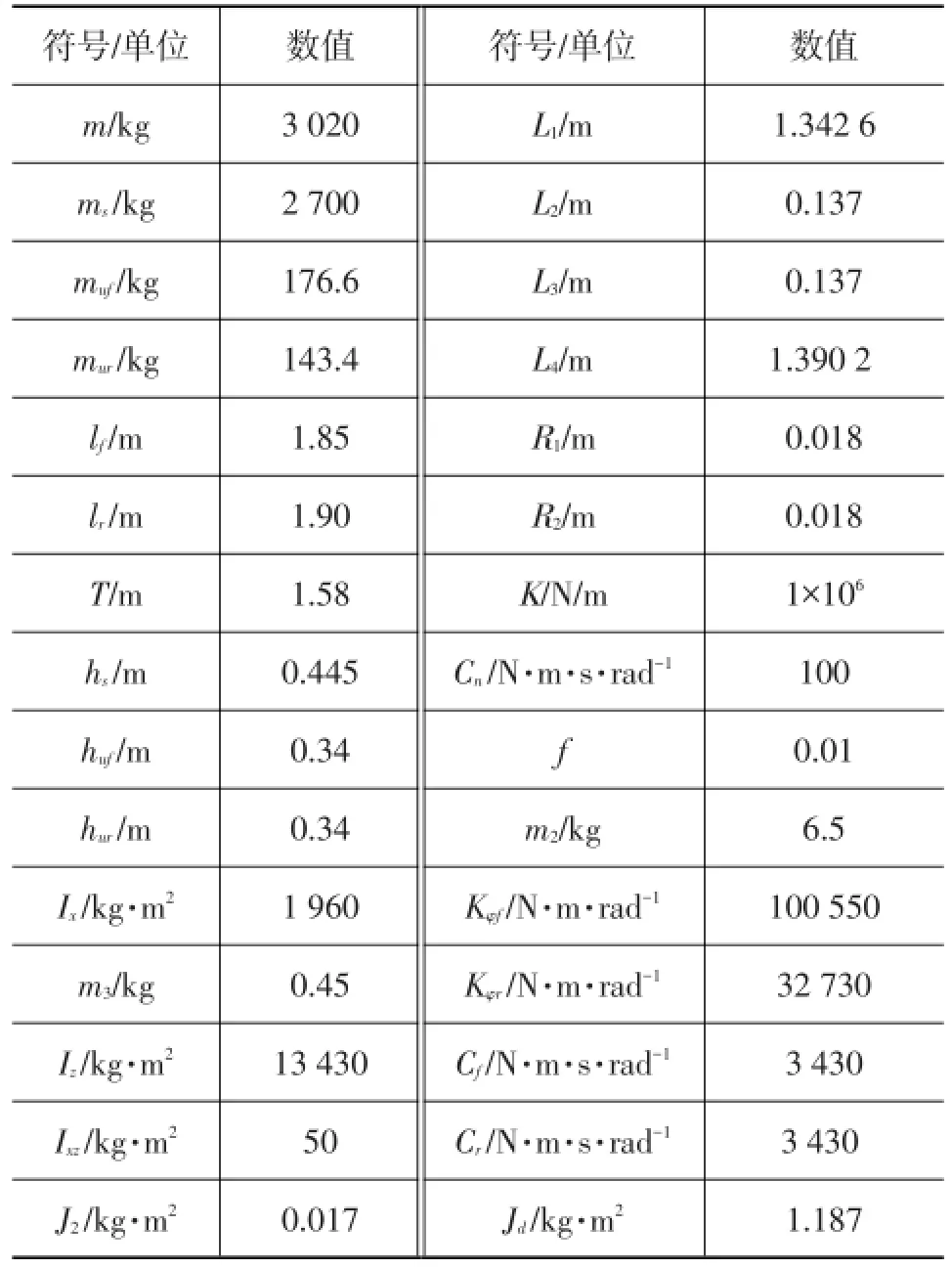
表2 样车计算所需主要参数

表3 不同间隙车辆失稳时质心侧偏角上下临界频率及带宽

由图3可以看出，当间隙r＜1.0 mm时，车辆蛇行工况一致性表现为单周期—混沌—倍周期—混沌—倍周期—单周期的复杂分叉行为；当间隙r＞1.0 mm时，蛇形工况两个混沌区域之间的倍周期区间消失，被混沌区域取代，车辆蛇形工况变为单周期—混沌—倍周期—单周期的分叉行为。

从图3和表3可以看出，随着间隙增大，车辆蛇行工况下整车质心侧偏角转向频率失稳上临界频率减小，下临界频率增大，且分叉行为中的倍周期过渡区间特征越来越不明显，最终消失。根据图3和表3数据可知，随着间隙r从0增加至2.0 mm，上临界频率f1由1.06 rad/s减小至0.99 rad/s，下临界频率f4由2.70 rad/s增加至3.62 rad/s，整个混沌失稳频率带宽由1.54 rad/s增加至2.63 rad/s。由此可知整车出现混沌失稳频率带宽随间隙增大而增加，这对于车辆安全行驶不利。当间隙r在0.5～1.0 mm范围内时，分叉频率带宽较小，理论上说明在设计转向机构球头间隙时r∈(0.5,1) mm范围有利于减小车辆蛇行失稳的几率。

3.2 对质心侧偏角频率特性β-f的相图分析

从图3可以看出，随着间隙增大，当f=2.8 rad/s时，汽车蛇形工况质心侧偏角分叉特性由倍周期逐渐过渡到混沌，故选取汽车蛇形工况进入单周期前的倍周期区域做频谱分析。取转角幅值A=1.5 rad、转角频率f= 2.8 rad/s，分别做出不同间隙下质心侧偏角的相图、庞加莱图和频谱图如图4所示。

从图4中可以看出，随着间隙r增大，质心侧偏角庞加莱图由孤立的两个点逐渐变为无规律的散点；频谱图中，主频成分幅值逐渐减小，出现一些幅值较小的其他成分，说明车辆质心侧偏角分叉行为由倍周期逐渐走向混沌。具体来看当间隙r=0.5 mm、1.0 mm时，相轨迹上仍表现出倍周期的特征，其频谱图上主频成分和副频成分清晰，随着间隙增加，轨迹线逐渐加粗，频谱图出现其他成分。当间隙r＞1.0 mm后，整车蛇形工况的动力学行为走向混沌，相轨迹已看不出周期特征，庞加莱图也变成无规则散点，频谱图上主频和副频成分已无法完全区分，车辆失稳行为表现得更加复杂。由此可能致使车辆在紧急工况下驾驶员急打转向盘而导致汽车甩尾、侧翻事故。因此，为了安全，应及时检查旧车转向系的球头间隙是否超值，保证合理的安全间隙。对于产品设计，应该从车辆蛇行工况安全的角度合理选取转向系球头间隙。

4 结束语

随着转向梯形间隙r的增大，整车系统分叉特性趋向混沌失稳，过渡倍周期区域逐渐减小直至消失，单周期区域减小，混沌区域增加。具体表现为随着间隙的增大，汽车蛇行失稳的上临界频率减小，而下临界频率加大，整个失稳的频率带宽相应加大，表明间隙r较大时增加了车辆蛇形失稳的概率。

理论上找到间隙r∈(0.5,1) mm区间时车辆蛇行工况失稳区间较小，这一范围在设计和制造上也易于实现，可为从车辆转向行驶稳定性角度考虑转向机构间隙设计提供参考。

1 卢剑伟，顾鴃，王其东.运动副间隙对汽车摆振系统非线性动力学行为影响分析.机械工程学报，2008（8）：169～173．

2 王威，宋玉玲，李瑰贤.独立悬架汽车转向系间隙与干摩擦对其Hopf分岔特性的影响.机械工程学报，2011，47（2）：130～135．

3 魏道高，王子涵，张翼天，肖怀阳.转向系间隙对操纵稳定性影响研究.汽车工程,2014,36（2）：139～144.

4 白争锋.含间隙机构接触碰撞动力学研究：[学位论文].哈尔滨：哈尔滨工业大学，2007．

5 Yuanyuan R,Xuelian Z,Xiansheng L.Handling Stability of Tractor Semitrailer Based on Handling Diagram.Discrete Dynamics in Nature&Society,2012.

6 Kim J.Effect of vehicle model on the estimation of lateral ve⁃hicle dynamics.International Journal of Automotive Tech⁃nology,2010,11（3）：331～337.

7 周兵，孙乐，左龙，等.考虑主销间隙的转向轮摆振研究.中国机械工程，2012，19：2286～2289．

8 郭孔辉.汽车操纵动力学原理.南京：江苏科学技术出版社,2011.

（责任编辑帘 青）

修改稿收到日期为2015年9月1日。

Study of the Effects of Steering Trapezoid Dual-clearance on Vehicle Stability under Slalom Maneuver

Wei Daogao1,Zhang Zhilong1,Jiang Tong1,Pan Zhijie2,Xiao Huaiyang2
（1.Hefei University of Technology;2.Zhejiang Geely Automobile Institute）

The steering trapezoid mechanism is simplified into a plane linkage mechanism,a four-DOF mathematical model of vehicle maneuvering system including body roll,yaw and sideslip and off front right wheel angle is established.On the basis of this model,a numerical analysis method is used to conduct a simulated analysis about the stability of prototype vehicle side slip angle as the double-clearance parameter of steering trapezoid motion pair changes.The results show that with the increase of the motion pair clearance,single cycle area of vehicle slalom motion decreases,whereas the perioddoubling area disappears and the chaos area increases.The instability interval under slalom maneuver is small in theory when the clearancesr＜1.0 mm.

Double Clearances，Slalom Maneuver，Sideslip Angle，Stability

双间隙 转向机构 蛇形工况 质心侧偏角 稳定性

U469.21

A

1000-3703（2015）10-0019-05