基于决策树雪花牛肉大理石花纹分级模型

梁 琨，丁 冬，彭增起，沈明霞,*，林盛业，曹 辉

（1.南京农业大学工学院，江苏 南京 210031；2.江苏省现代设施农业技术与装备工程实验室，江苏 南京 210031；3.南京农业大学食品科技学院，江苏 南京 210095；4.陕西秦宝牧业股份有限公司，陕西 宝鸡 721000）

基于决策树雪花牛肉大理石花纹分级模型

梁 琨1,2，丁 冬1，彭增起3，沈明霞1,*，林盛业1，曹 辉4

（1.南京农业大学工学院，江苏 南京 210031；2.江苏省现代设施农业技术与装备工程实验室，江苏 南京 210031；3.南京农业大学食品科技学院，江苏 南京 210095；4.陕西秦宝牧业股份有限公司，陕西 宝鸡 721000）

为建立雪花牛肉大理石花纹等级评价方法，根据不同等级雪花牛肉大理石花纹图像特征及人工评级的标准，确定了影响大理石花纹的等级主要因素。本研究提出影响大理石花纹等级的几何参数特征、几何分布参数特征和统计参数特征。其中几何参数特征主要反映大理石花纹面积、周长等；几何分布特征主要反映大理石花纹图像中脂肪颗粒沉积的密度，根据脂肪颗粒沉积情况可分为大颗粒脂肪、中颗粒脂肪、小颗粒脂肪等；统计参数特征主要反映大理石花纹丰富程度以及大理石花纹分布均匀性。利用相关性分析提取影响雪花牛肉大理石花纹等级的特征参数。建立基于C4.5和CART算法的决策树模型，结果表明：对于C4.5算法建立的决策树分级模型，三级和五级大理石花纹分级预测精度分别为91.80%、92.31%，而该模型针对四级样本建立的模型无效，其结果多数误判为三级；对于CART算法建立的决策树模型同样存在这样的问题，即三级和五级大理石花纹分级预测精度高，而对四级样本分级无效。

雪花牛肉；大理石花纹；分级模型；决策树

雪花牛肉作为我国高档牛肉，富含高浓度亚油酸以及钙磷铁等矿物质，牛的背最长肌中沉积了雪花状的丰富脂肪，这种分布形成了类似大理石花纹图案[1-2]。脂肪分布量不同，其大理石花纹等级亦不相同，脂肪分布越多，等级越高[3-4]，因此大理石花纹可以作为评定雪花牛肉品质主要指标。近年来随着人们生活水平的不断提高，对雪花牛肉的需求量也不断增大，而雪花牛肉等级不同其经济价值差别亦较大[5]。目前雪花牛肉分级主要采用人工分级，存在主观性强、易产生视觉疲劳等缺点[6]，因此研究雪花牛肉大理石花纹等级识别方法对规范雪花牛肉市场、提高生产效率有重要意义。

机器视觉技术被广泛应用于牛肉自动分级检测领域。Shiranita等[7]提取了牛肉大理石花纹图像中肌内脂肪面积比、脂肪颗粒总数、大脂肪颗粒数、小脂肪颗粒数以及脂肪分布系数，作为图像特征分析结构表明牛肉大理石花纹等级与肌内脂肪面积比、大脂肪颗粒数和脂肪分布系数之间显著相关。Jeyamkondan等[8]将牛胴体眼肌肌内脂肪的面积、周长以及脂肪颗粒数作为判定牛肉大理石花纹等级的特征参量，并且通过多元回归分析得到数学模型与由专业牛肉质量评定师判定的结果是等价的。孟祥艳[9]提取牛肉大理石花纹图像的几何、粒度及形状参数来表征花纹几何、形状及分布特点，利用主成分分析法对影响大理石花纹等级的参数进行线性组合，建立大理石花纹的等级预测模型。周彤等[10]为评价大理石花纹的丰富程度，提取大理石花纹面积比值、大脂肪颗粒个数和密度、中等脂肪颗粒个数和密度、小脂肪颗粒个数和密度、总脂肪颗粒个数和密度、脂肪分布均匀度10个指标为特征参数对牛肉大理石花纹进行评。陈坤杰等[11-12]利用牛肉大理石花纹的面积比率、总脂肪颗粒数、大小脂肪颗粒数以及每个牛肉大理石花纹样本图像的计盒维数和信息维数这些参数为基础，分别建立了牛肉大理石花纹等级判定的多元线性模型和多元多项式模型。

针对我国雪花牛肉大理石花纹的分级研究，研究学者取得了一定成果。刘超超[13]、李小林[6]等研制的基于嵌入式机器视觉技术雪花牛肉等级分级系统，研究了屠宰车间生产环境中的胴体雪花牛肉图像采集系统，并利用图像处理方法进行了预处理、提取了大理石花纹图像的花纹面积、周长等特征。马鹏鹏[14]研究了基于凹点检测方法的雪花牛肉大理石花纹图像分割。刘璎瑛等[15]提出用粗糙度和细密度来定量描述脂肪的分布特征，并研究了两个指标能够随雪花牛肉大理石花纹脂肪含量的变化情况。但是针对雪花牛肉大理石花纹分级模型的研究相对较少。

本实验在前人研究基础上，提出了影响雪花牛肉大理石花纹等级的几何参数、几何分布参数和统计参数特征，分析每个特征大理石花纹等级之间的相关性，从而选择建模有效的特征变量。研究利用决策树方法建立雪花牛肉大理石花纹分级模型，分别建立基于C4.5算法和CART算法模型，比较两种算法的预测精度，从而建立分级效果较好的决策树模型。

1 材料与方法

1.1数据采集

本研究实验数据采集于2012年5月—2013年7月期间在陕西秦宝牧业进行，所选用雪花牛肉样本来自陕西本地秦川牛与日本和牛、澳大利亚安格斯牛三元杂交肉牛，样本屠宰后在冷库车间排酸72 h后分割二分体。雪花牛肉眼肌横切面图像的获取采用南京农业大学自主研发的基于机器视觉雪花牛肉采集系统，实验时采集牛胴体二分体第6至7根肋骨眼肌横切面图像，为保证图像样本的有效性和一致性，实验保持眼肌表面切割平整，无明显刀痕、碎肉沫、水分等干扰，尽量保证不要有外界光线进入采集密闭装置，并使整个眼肌区域完整的处于采集图像中心位置。实验共采集有效样本222幅，其中一级至五级图像样本数量分别为15、75、88、25、19；样本总量成正态分布，这与企业实际雪花牛肉生产数量相吻合。每一幅图像人工等级根据日本雪花牛肉评级标准图版进行5个等级评定，最终结果为两个或两个以上评级员所评等级。利用图像处理算法，将采集样本图像经过灰度化、滤波、图像增强、眼肌区域提取，大理石花纹提取等预处理[6]。

1.2图像特征提取与选择

1.2.1特征提取

通过比较不同等级雪花牛肉大理石花纹图像特征及人工评级的标准，确定影响大理石花纹的等级主要因素。本研究提出影响大理石花纹等级的几何参数特征、几何分布参数特征和统计参数特征。其中几何参数特征主要反映大理石花纹面积、周长等[6]；几何分布特征主要反映大理石花纹图像中脂肪颗粒沉积的密度，根据脂肪颗粒沉积情况可分为大颗粒脂肪、中颗粒脂肪、小颗粒脂肪等[10,12,16]；统计参数特征主要反映大理石花纹丰富程度以及大理石花纹分布均匀性[15,17]。表1为提取的雪花牛肉大理石花纹图像18个特征。

表1 雪花牛肉大理石花纹图像特征变量Table1 Image features of snowflake beef marbling

雪花牛肉大理石花纹图像的几何参数特征是根据眼肌区域的大理石花纹的几何特征进行描述。眼肌总像素定义为图像二值化算法处理后眼肌区域内包括所有像素总和；眼肌面积为单位像素所对应实际样本的面积（cm2）与眼肌区域总像素乘积；大理石花纹含量为眼肌区域代表脂肪颗粒所有黑色联通区域像素总和与眼肌区域总像素比；大理石花纹周长定义眼肌面积内所有代表脂肪颗粒所有黑色联通区域周长总和；轮廓面积比定义为大理石花纹周长比眼肌面积；轮廓周长比定义为大理石花纹周长比眼肌周长。

根据采用硬件相机的放大倍数下所拍摄的眼肌图片与人眼观测下的眼肌花纹辨析度，确定本研究中颗粒脂肪定义。其中，小颗粒脂肪数量为孤立的连通区域像素个数在20～50个像素之间的连通区域个数；中颗粒脂肪数量为孤立的连通区域像素个数在50～450个像素之间的连通区域个数；大颗粒脂肪数量为孤立的连通区域的像素个数在450个像素以上的连通区域个数。小颗粒数量密度为小颗粒的总像素/眼肌总像素，小颗粒分布密度为小颗粒的总个数比眼肌区域面积（cm2）；中颗粒与大颗粒数量密度和分布密度定义与之类似。

统计参数特征定义根据脂肪面积差异均匀性和脂肪数量及位置分布均匀性。粗糙度主要指大理石花纹中各个脂肪面积之间的差异性，大理花纹脂肪颗粒面积分布越不均匀，其粗糙度越大。细密度主要表示大理石花纹中脂肪数量的分布，大理石花纹面积相同的样本中，脂肪颗粒数量越多，其大理石花纹细密度越大。大理石花纹粗糙度及细密度测量参照文献中方法计算[15]，公式（1）为粗糙度（C）计算公式，公式（2）为细密度（F）计算公式，脂肪颗粒相对标准差表示脂肪分布均匀度，也即脂肪颗粒分布变异系数（α），计算方法如公式（3）所示。

式中：n为大理石花纹中提取的脂肪数量；[M1, M2,…, Mn]为各个脂肪的面积；为脂肪平均面积；Sr为有效切面的面积。

1.2.2特征选择

为了保证利用高效的特征变量建立模型，本实验研究提取的雪花牛肉图像特征变量与人工评定等级之间的相关性分析，根据相关系数选择针对有效模型的特征变量，相关系数（r）计算如公式（4）所示。

式中：n为样本总数；xi为特征变量中第i个样本；为特征变量样本平均值；yi为等级变量第i个样本；为等级样本平均值。

1.3决策树模型建立

在建立决策树模型时，根据分裂准则的不同，可采用基于信息论（information theory）和最小GINI指示（lowest GINI index）两种方法[18]。本实验分别采用基于信息论方法构建C4.5算法和基于最小GINI指示方法构建CART算法建立雪花牛肉大理石花纹分级模型，比较两种算法的训练集样本和验证集样本的分级准确率，选择较好的决策树模型。为保证模型的准确性而不出现过拟合的现象，选择10折交叉验证（10-fold cross validation）估算训练集建立模型的准确率。

1.3.1基于C4.5算法决策树模型

C4.5算法计算信息增益比来确定每个节点的分类属性，每个节点军训则具有最高信息增益比的属性作为前节点的分裂属性。这种属性选择方法使之后生成决策树对训练样本进行分类时所需信息最小。C4.5算法流程如下[19-20]：1）创建节点N；2）如果训练样本T都属于同一类C，则N为叶节点，标记为类C；3）如果训练样本的属性数为空，即没有属性进行分裂，则T为叶节点，标记该节点为T中出现最多的类；4）如果不满足2）、3），则计算训练样本T各属性信息增益率：假设T是一个训练样本，样本总量n属于m各类别，其中第i个类在T中出现的比例为Pi，则T的信息熵（I（T））计算公式如下。

若属性A将T划分为v个子集{T1,T2,…, Tv}，其中Ti包含样本数ni，则划分后熵（E（A））计算公式如下。

分裂后的信息增益（Gain（T，A））计算公式如下。

训练样本T关于属性A的各取值的熵计算公式如下。

式中：Ti为训练样本T中A属性第i各取值对应的子集，属性A划分v个子集。则信息增益比计算公式如下。

5）选择各属性中具有最高信息增益率的属性作为分裂属性，将训练样本分割；该属性的各个取值对应生成心的子节点；6）对每个从节点N长出的新子节点进行判断。如果叶节点对应的子集为空，则分裂该叶节点生成一个新叶节点，否则在该子节点上重复步骤2）、6）继续分裂；7）计算每个节点分类错误，进行剪枝；8）建立最终决策树模型。

1.3.2 基于CART算法决策树模型

CART算法最早由Breiman等[21]提出，是一种有监督学习算法，可以处理高度倾斜或多态的数值型数据。CART使用二叉树将预测空间递归地划分为若干子集，树中的叶节点对应于不同的划分区域，划分是由与每个内部节点相关的分支规则确定的。通过从根节点到叶竹点的路径，一个预测样本就被赋予一个唯一的叶节点，类别也就得到确定[22]。在此算法中[23-24]，对于每个属性，执行该属性上的一个划分，计算划分GINI系数。

式中：pj为训练样本集T包含j的概率，若N属性中具有最小GINI系数的属性，划分T为T1、T2子集，此时划分的GINI系数为：

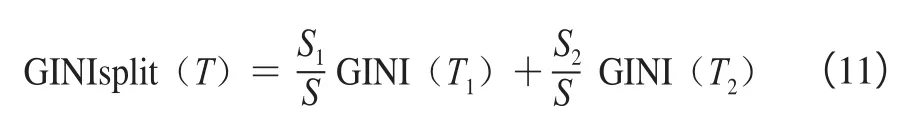
式中：S为T样本个数，S1、S2分别为T1、T2的样本个数。

1.4数据处理

图像处理及特征提取程序采用VC++6.0编写。利用SPSS 16.0软件进行数据统计及相关性分析选择决策树建模有效的特征变量；决策树模型C4.5和CART算法利用MATLAB 2012a软件编写。

2 结果与分析

2.1图像特征提取及选择

提取的雪花牛肉大理石花纹图像特征能否如实反映花纹等级取决于特征与等级之间的契合度。为了衡量提取的图像特征的评级有效性，利用SPSS 16.0软件对提取的18 个图像特征与大理石花纹等级进行相关性分析，其分析结果如表2所示。眼肌总像素（V1）、眼肌面积（V2）、小颗粒脂肪个数（V7）、小颗粒脂肪数量密度（V8）、小颗粒脂肪分布密度（V9）这5 个特征变量与大理石花纹等级在α=0.05显著水平下没有显著相关性。大理石花纹含量（V3）和大颗粒脂肪数量密度（V14）与等级之间相关性较高，相关系数分别为0.906、0.879。因此本研究利用除去眼肌总像素（V1）、眼肌面积（V2）、小颗粒脂肪个数（V7）、小颗粒脂肪数量密度（V8）、小颗粒脂肪分布密度（V9）这5 个特征剩下的13 个特征建立决策树分级模型。

表2 雪花牛肉大理石花纹图像特征与等级相关性分析Table2 Correlation analysis of snowflake beef marbling image features with graddeess

2.2决策树模型建立

实验共采集有效样本222幅，其中一级至五级图像样本数量分别为15、75、88、25、19；本研究为了建立模型的有效性、准确性，分别从每个等级取70%样本作为训练集样本，取每个等级样本的30%作为验证集样本。直接用连续属性对决策树节点进行分支，会产生大量的子节点，而且这些子节点基本多是纯节点，即每个新产生的节点中的数据都属于同一类无法再分。这将导致决策树过度细化，直接影响分类器的分类性能[25]。因此本研究采用无监督等宽方法对提取的13个有效特征进行离散化，即将每个特征取值按照最小到最大值的值域等分10份，然后将每个特征取值按照不同区间映射到不同的离散值。利用10折交叉验证方法建立决策树C4.5和CART算法模型。

基于C4.5算法建立的决策树模型枝叶节点个数为28，其模型算法描述如下：

基于CART算法建立的决策树模型枝叶节点个数为4，其模型算法描述如下：

表3和表4分别为基于C4.5和CART算法建立决策树模型分级结果，由表3、4可知，基于C4.5算法建立的决策树识别模型训练样本分级准确率为76.92%，验证样本分级准确率为71.21%；其结果分别低于基于CART算法建立的模型准确率（训练样本77.56%，验证样本74.24%）。因此，基于CART算法的决策树模型优于C4.5算法的模型。

对于C4.5算法建立的决策树分级模型，三级和五级大理石花纹分级预测精度高（分别为91.80%、92.31%），而该模型针对四级样本建立的模型无效，其结果多数误判为三级；对于CART算法建立的决策树模型同样存在这样的问题，即三级和五级大理石花纹分级预测精度高，四级样本分级无效。主要原因：其一，雪花牛肉大理石花纹高端等级样本比较少，因此在样本采集时限制了样本数量；其二，决策树模型在三级、四级样本预测时存在缺陷，因此在今后的工作中需要进一步研究更适合雪花牛肉大理石花纹分级的模型。

表3 基于C4.5算法的决策树模型分级结果混淆矩阵Table3 Confusion matrix of decision tree classification results based on C4.5 algorithhmm

表4 基于CART算法的决策树模型分级结果混淆矩阵Table4 Confusion matrix of decision tree classification results based on CART algoritthhmm

3 结 论

根据雪花牛肉大理石花纹图像特征及人工评级的标准，提取影响大理石花纹的等级主要特征因素，包括几何参数特征、几何分布参数特征和统计参数特征的18个特征变量。分析大理石花纹图像特征与等级之间的相关性，确定表征雪花牛肉大理石花纹等级的有效特征变量，分析结果表明除去眼肌总像素（V1）、眼肌面积（V2）、小颗粒脂肪个数（V7）、小颗粒脂肪数量密度（V8）、小颗粒脂肪分布密度（V9）这5个特征剩下的13个特征为分级有效特征。

为提高模型的精确度，对13个特征进行离散化预处理后建立10折交叉训练模型。分别利用C4.5算法和CART算法建立决策树分级模型，两种算法对应的训练模型预测精度分别为76.92%、77.56%；验证样本的预测精度分别为71.21%、74.23%。因此由此可知CART算法建立的决策树模型精度比C4.5算法建立模型精度高。但是决策树模型预测三级和五级大理石花纹分级预测精度高（均高于90%以上），而对四级样本分级无效。

[1] 桑国俊, 程强. 我国雪花牛肉生产现状与分析[J]. 中国牛业科学, 2013, 39(2)∶ 1-5.

[2] 丁君辉, 周萍芳, 杨眉. 我国肉牛产业的发展现状[J]. 江西畜牧兽医杂志, 2012(2)∶ 6-8.

[3] CRAIGIE C R, NAVAJAS E A, PURCHAS R W, et al. A review of the development and use video image analysis for beef carcass evaluation as an alternative to the current ETROP system and other subjective systems[J]. Meat Science, 2012, 92(4)∶ 307-318.

[4] 徐玉玲. 日本和牛×秦川牛×安格斯牛三元杂交雪花牛胴体质量及肉质分析[D]. 兰州∶ 甘肃农业大学, 2013.

[5] 张路培, 袁峥嵘. 中国高档牛肉市场现状及发展趋势展望[J]. 中国畜牧杂志, 2012, 48(4)∶ 34-40.

[6] 李小林. 嵌入式机器视觉技术在雪花牛肉品质检测中的应用研究[D].南京∶ 南京农业大学, 2013.

[7] SHIRANITA K, HAYASHI K, OTSUBO A, et al. Gradingmeat quality by image processing[J]. Patten Recognition, 2000, 33∶ 97-104.

[8] JEYAMKONDAN S, RAY N, KRANZLER G A, et al. Beef quality grading using machine vision[C]//Conference on Biological Quality and Precision Agriculture Ⅱ, Boston, USA∶ IEEE, 2000∶ 91-101.

[9] 孟祥艳. 牛眼肌区域大理石花纹评级特征的研究[J]. 肉类研究, 2011, 25(10)∶ 6-11.

[10] 周彤, 彭彦昆. 牛肉大理石花纹图像特征信息提取及自动分级方法[J].农业工程学报, 2013, 29(15)∶ 286-293.

[11] 陈坤杰, 姬长英. 基于图像运算的牛肉大理石花纹分割方法[J]. 农业机械学报, 2007, 38(5)∶ 195-196.

[12] 陈坤杰, 吴贵茹, 於海明, 等. 基于分形维和图像特征的牛肉大理石花纹等级判定模型[J]. 农业机械学报, 2012, 43(5)∶ 147-151.

[13] 刘超超, 彭增起, 沈明霞, 等. 牛胴体品质检测系统中基于嵌入式Linux的终端设计[J]. 食品工业科技, 2012, 33(7)∶ 336-339.

[14] 马鹏鹏. 雪花牛肉眼肌切面图像处理与检测算法研究[D]. 南京∶ 南京农业大学, 2014.

[15] 刘璎瑛, 沈明霞, 彭增起, 等. 雪花牛肉大理石花纹粗糙度和细密度的测定[J]. 食品科学, 2013, 34(18)∶ 170-174. doi∶10.7506/spkx1002-6630-201318034.

[16] 李玮姿, 朱近, 杨德吉. 基于图像的牛肉大理石纹理自动评级方法研究[J]. 食品科学, 2011, 32(9)∶ 40-45.

[17] KUCHIDA K. Objective measurement of beef meat quality bycomputer image analysis method[C]//2011 International Conference on Beef Castle Improvement and Industrialization in China. Beijing, 2011.

[18] 元昌安. 数据挖掘原理与SPSS Clementine应用[M]. 北京∶ 电子工业出版社, 2009∶ 147-149.

[19] 丁胜祥. 基于决策树算法的洪水预报模型[J]. 水利发电, 2011, 37(7)∶ 8-12.

[20] SUN Weixiang, CHEN Jin, LI Jiaqing. Decision tree and PCA-based fault diagnosis of rotating machinery[J]. Mechanical Systems and Signal Processing, 2007, 21(3)∶ 1300-1317.

[21] BREIMAN L, FRIEDMAN J, OLSHEN R A, et al. Classification and regression trees[M]. Belmont∶ Wadsworth, 1984∶ 1-358.

[22] 李琳. 基于决策树的数据挖掘方法在化学模式分类中的应用[D]. 杭州∶ 浙江大学, 2005.

[23] 程铁信, 郭涛, 祁昕. 决策树分类模型在工程项目评标风险预警中的应用[J]. 数理统计与管理, 2010, 29(1)∶ 122-128.

[24] TURE M, TOKATLI F, KURT I. Using Kaplan-Meier analysis together with decision tree methods (CART, CHAID, QUEST, C4.5 and ID3) in determining recurrence-free survival of breast cancer patients[J]. Expert Systems with Applications, 2009, 36∶ 2017-2026.

[25] 李春贵, 王萌, 孙自广, 等. 属性频率划分和信息熵离散化的决策树算法[J]. 计算机工程与应用, 2009, 45(12)∶ 153-156.

Classification of Snowflake Beef Marbling Grades Based on Decision Tree

LIANG Kun1,2, DING Dong1, PENG Zengqi3, SHEN Mingxia1,*, LIN Shengye1, CAO Hui4(1. College of Engineering, Nanjing Agricultural University, Nanjing 210031, China; 2. Jiangsu Province Engineering Laboratory for Modern Facility Agriculture Technology and Equipment, Nanjing 210031, China; 3. College of Food Science and Technology, Nanjing Agricultural University, Nanjing 210095, China; 4. Limited Liability Company of Qin Bao Animal Husbandry in Shaanxi Province, Baoji 721000, China)

In order to establish a method to evaluate snowflakes beef marbling grades, the main factors affecting grading marbling were identified by comparing the image features with artificial rating criteria of different snowflakes beef marbling grades. This study presented the geometric feature parameters, geometric distribution feature parameters and statistical feature parameters affecting marbling grade. The geometric feature parameters mainly reflected the marbling area, perimeter and so on. The geometric distribution feature parameters mainly reflected the different deposition densities of large, medium and small fat particles in the marbling image. The statistical feature parameters mainly reflected the marbling abundance and marbling distribution uniformity. Correlation analysis between the features parameters extracted and snowflake beef marbling grades was conducted. Decision tree models were established based on C4.5 and CART algorithm, and the results showed that the prediction accuracy of three-level and five-level grades were 91.80%and 92.31%, respectively, however, the model for the four-level sample model was invalid and the misjudgment results were mostly three-level. The same problem existed in the prediction accuracy of models based on CART algorithm.

snowflake beef; marbling; classification model; decision tree

TS251.3

1002-6630（2015）17-0065-06

10.7506/spkx1002-6630-201517013

2015-02-03

国家现代农业（肉牛）产业技术体系建设专项（CARS-38）；中央高校基本科研业务费专项资金项目（KJQN201557）；农业科技成果转化资金项目（SQ2011ECC100043）；南京农业大学科研启动基金项目（RCQD13-15）

梁琨（1983—），女，讲师，博士，主要从事农产品检测技术研究。E-mail：lkbb2006@126.com

*通信作者：沈明霞（1964—），女，教授，博士，主要从事检测技术自动化装置研究。E-mail：mingxia@njau.edu.cn