连续变化内压下套管-水泥环-围岩组合体微环隙计算

初纬，沈吉云，杨云飞，李勇，高德利

（1.中国石油集团钻井工程技术研究院；2.中国石油大学（北京）；3.Stanford University）

连续变化内压下套管-水泥环-围岩组合体微环隙计算

初纬1,2，沈吉云1，杨云飞3，李勇1，高德利2

（1.中国石油集团钻井工程技术研究院；2.中国石油大学（北京）；3.Stanford University）

固井后井筒内压力的变化可能导致水泥环破坏或使水泥环产生塑性变形，从而在第一界面或第二界面处产生微环隙。基于Mohr-Coulomb准则，建立了套管-水泥环-围岩组合体弹塑性分析模型，对套管内压力加载和卸载过程进行分析，以界面拉力大小判定是否产生微环隙，并给出了微环隙大小的计算公式。使用该模型对前人的气窜实验进行模拟，理论结果与实验结果相符。分析结果表明，微环隙的产生由加载和卸载过程共同决定。加载过程可能会使水泥环进入塑性，而卸载时内压降低将导致界面受拉，从而产生微环隙。第一界面、第二界面均可能产生微环隙，取决于界面胶结强度与界面拉力的关系。卸载时，第一界面拉力大于第二界面拉力，当两个界面胶结强度接近时，第一界面更容易产生微环隙。该模型可用于评价水力压裂等过程中水泥环密封失效的风险，为现场施工提供依据，从而降低井筒密封完整性失效的风险。图6表1参10

套管-水泥环-围岩微环隙；井筒完整性；弹塑性特征；胶结强度；套管内压力加载；套管内压力卸载

0 引言

固井水泥环密封失效将引起地层流体泄漏，导致套管间环空带压，严重影响油气井正常生产，造成油气资源的浪费。对于水泥环密封完整性的研究，早期集中于水泥环本身的破坏，即拉张、剪切破坏。从20世纪90年代开始，研究者通过一系列实验发现[1-3]，在固井后的生产过程中（如油气井试压、页岩气井压裂以及储气库井注采等），井筒内压力变化亦可导致在第一界面（水泥环-套管界面）或第二界面（水泥环-围岩界面）产生环空微间隙（下称微环隙），从而造成水泥环密封完整性失效。

由于组合体的复杂性，目前的研究多采用有限元方法[4-5]。在理论分析方面：殷有泉、万曦超等给出了套管-水泥环-围岩组合体的弹性解析解[6-7]；陈朝伟等采用Mohr-Coulomb准则建立了套管-地层组合体的弹塑性理论公式[8]，结果表明，套管荷载的塑性解与弹性解差距可达6%；李军等采用Tresca准则讨论了套管-水泥环-围岩组合体的弹塑性理论公式[9]。以上研究均侧重于组合体在一定外力下的应力、应变分析，对界面微环隙的研究相对较少，尤其缺少定量描述微环隙生成和发展的力学模型。

本文采用Mohr-Coulomb准则，建立了考虑水泥环塑性特征及界面胶结强度的套管-水泥环-围岩组合体力学模型。通过模拟水力压裂等施工作业中套管内压力先上升（加载）后下降（卸载）的过程，分析微环隙产生的原因、推导计算变内压下界面微环隙大小的理论公式，并采用文献中组合体完整性模拟实验数据对模型进行验证。

1 模型建立

施工作业中，随着套管内压力的加载，水泥环与套管产生向外膨胀的径向位移。若加载压力较大，水泥环将产生不可恢复的塑性形变，导致套管内压力卸载时水泥环-套管或水泥环-地层界面受拉，当该拉应力大于界面胶结强度时，将导致界面脱离，产生微环隙。

本文对套管内压力加载和卸载过程分别进行计算，根据加载阶段组合体各点的应力状态与位移大小计算卸载后水泥环界面接触力的大小，判断是否发生界面脱离，最后建立计算变内压作业时微环隙的理论模型。

1.1 套管内压力加载阶段套管-水泥环-围岩组合体力学模型

建立厚壁圆筒平面应变问题的模型，假设套管和围岩均为弹性体，水泥环为理想弹塑性体，屈服条件满足Mohr-Coulomb准则。随着作业压力的升高，水泥环内壁处首先屈服并进入塑性。若压力继续增加，则水泥环塑性区由内壁处沿径向向外逐渐扩大，水泥环被分为塑性区和弹性区（见图1）。当内压超过某临界值后，水泥环完全进入塑性状态，不存在弹性区。

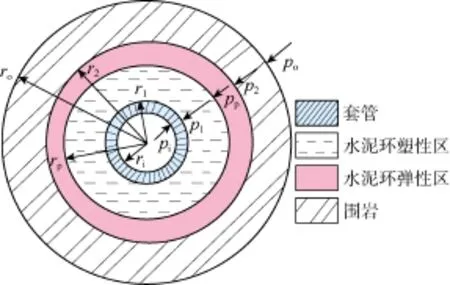
图1 水泥环部分进入塑性状态组合体模型

本文仅给出水泥环弹塑性状态下的计算过程，水泥环完全进入塑性的计算方法与之相似。对套管、水泥环和地层分别求解，并利用边界连续条件解出水泥环弹性区、塑性区界面位置rp以及界面接触力p1、pp、p2，从而求出系统各点的应力、位移大小。

1.1.1 套管（ri≤r≤r1）

套管在变内压下始终为弹性体。根据拉梅公式[9]，套管外壁处的径向位移为：

1.1.2 水泥环塑性区（r1≤r≤rp）

选取Mohr-Coulomb准则作为水泥环的塑性屈服准则，则：

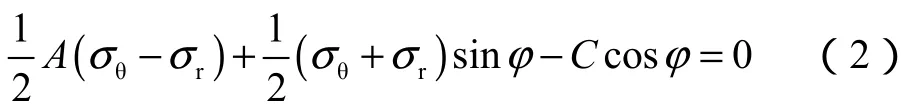
式中参数A用于区分最大、最小主应力，当σθ＞σr时，A=1，当σθ≤σr时，A =-1。

对于满足该准则的单一环体，其应力-应变关系详细推导可见文献[8]，本文仅给出简要过程。同时，水泥环满足平衡方程：

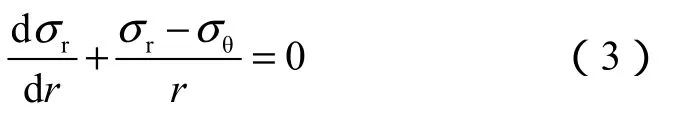
联立（2）式和（3）式，考虑边界条件r = r1时，σr=-p1，解得水泥环塑性区的应力分布表达式：

再利用边界条件r = rp时，σr=-pp，解得水泥环弹塑性界面处的受力大小：

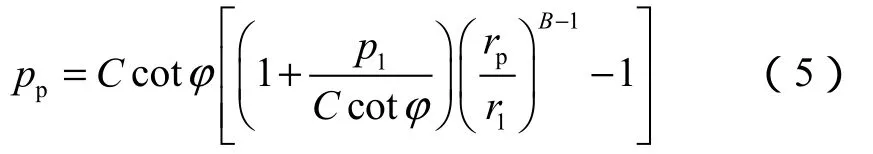
忽略塑性体应变，由体积弹性定律可得[8,10]：

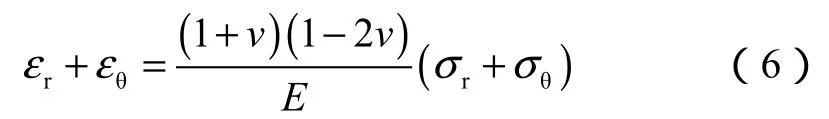
由几何方程：

将（4）式、（7）式代入（6）式，积分得到水泥环塑性区位移ucp的表达式：

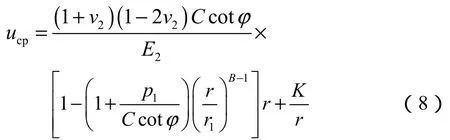
（8）式中K为积分常数，为未知量。由（8）式可得，水泥环塑性区内、外边界的位移分别为：

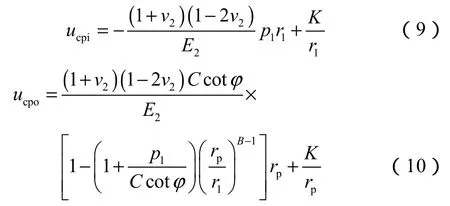
1.1.3 水泥环弹性区（rp≤r≤r2）

水泥环弹性区内壁压力为pp、外壁压力为p2。根据拉梅公式[10]，弹塑性边界r = rp处的应力为：

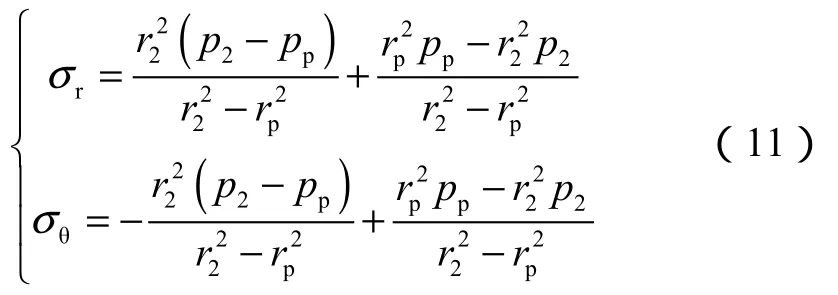
在r = rp处水泥环同时也满足屈服准则，联立（2）式和（11）式，得到水泥环-围岩界面的接触力为：

根据厚壁圆筒径向位移公式，水泥环弹性区内、外边界处的径向位移为：

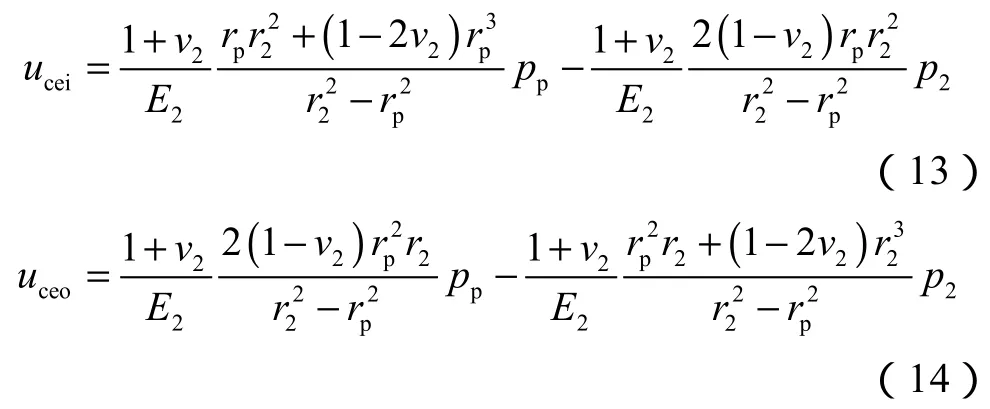
1.1.4 井壁围岩（r2≤r≤ro）

井壁围岩内壁压力为p2、外壁压力为po。其内壁处的径向位移为：

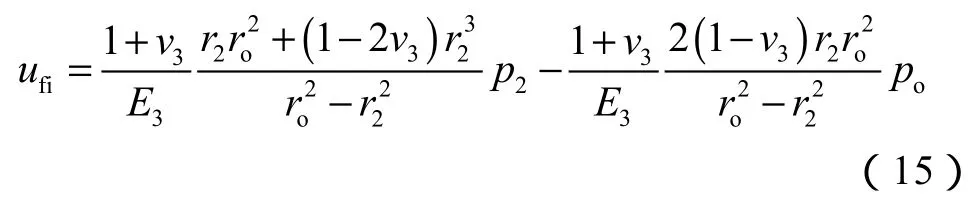
加载阶段，套管、水泥环、地层各部分紧密相联，在第一界面、水泥环弹塑性界面和第二界面处均满足径向位移的连续条件，由（1）式、（9）式、（10）式、（13）—（15）式以及（5）式、（12）式，可得到套管-水泥环-围岩组合体在水泥环弹塑性状态下的方程组：

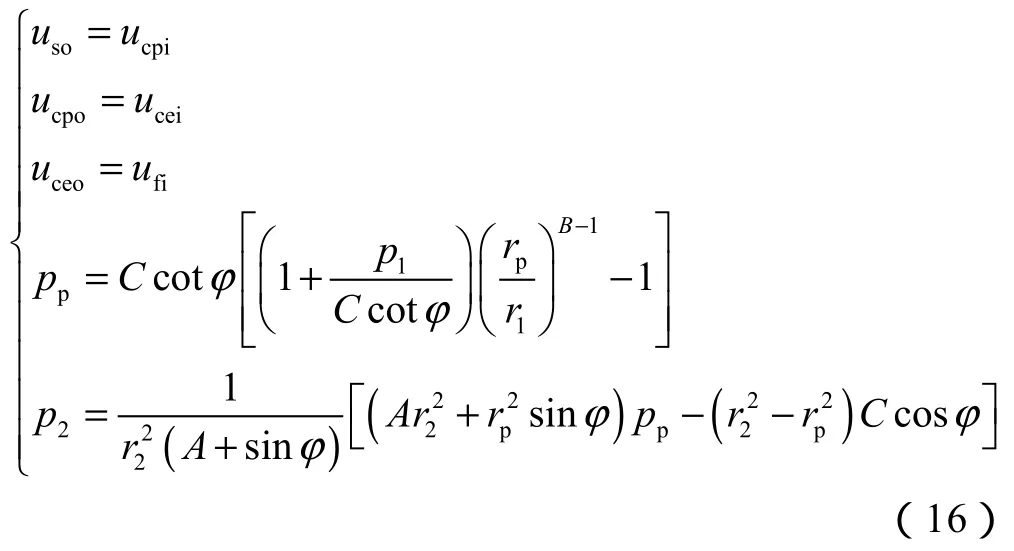
（16）式是关于p1、pp、p2、rp和K的五元方程组，在已知套管-水泥环-围岩组合体受到的内压pi和外压po的情况下，可以通过该方程组求解压力加载阶段组合体各点的应力状态和位移大小。

1.2 套管内压力卸载阶段界面脱离判断

由塑性力学可知，塑性材料在卸载时应力和应变的关系也是线性的，且其斜率与加载时的弹性阶段基本相同[10]。因此本文假设在套管内压力降低的过程中，套管、水泥环、地层均为弹性卸载，套管内压力降低造成的组合体应力、应变改变量可由弹性力学方法求得。卸载过程中，水泥环界面所受压力逐渐减弱，当界面由受压状态转变为受拉状态，且拉应力超过界面胶结强度时，将会产生微环隙。

设套管内压力先升高至pim，此时水泥环内壁处压力p1m、水泥环外壁处压力p2m等参数均可由上文模型求出。其后套管内压力卸载至pin，与之对应的水泥环内壁处压力p1n、外壁处压力p2n等参数需重新求解。

套管始终为弹性体，卸载后内压为pin、外压为p1n。其外壁处的径向位移为：

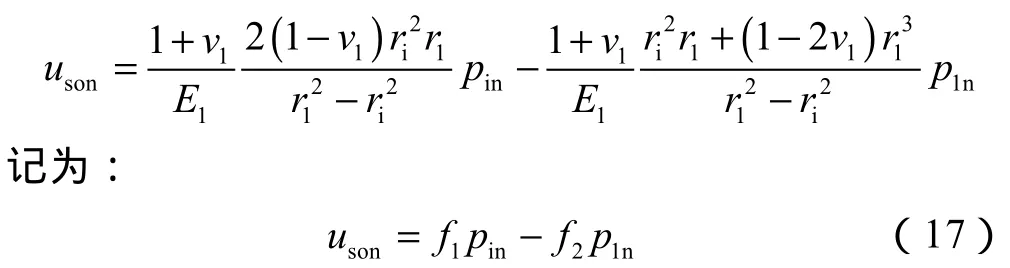
同理，井壁围岩内壁处压力为p2n、外边界压力为po。其内壁径向位移：

卸压后，水泥环内壁压力为p1n、外壁压力为p2n。内壁径向位移ucin为加载时产生的位移ucpim（塑性区内边界位移）与卸载时内壁的形变改变量ucir之和，ucir可由厚壁圆筒弹性理论得到，即：

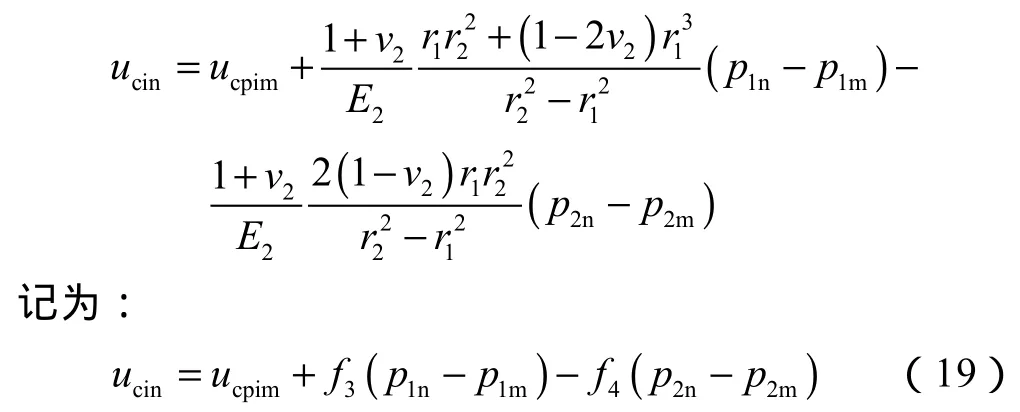
同理，可以得到水泥环外壁卸压后的径向位移：

假设压力卸载至pin时胶结强度足够大，未使界面发生脱离，则组合体仍满足界面处的径向位移连续条件：

将（17）、（18）、（19）、（20）式代入（21）式，可以求出界面脱离前第一界面、第二界面处压力：

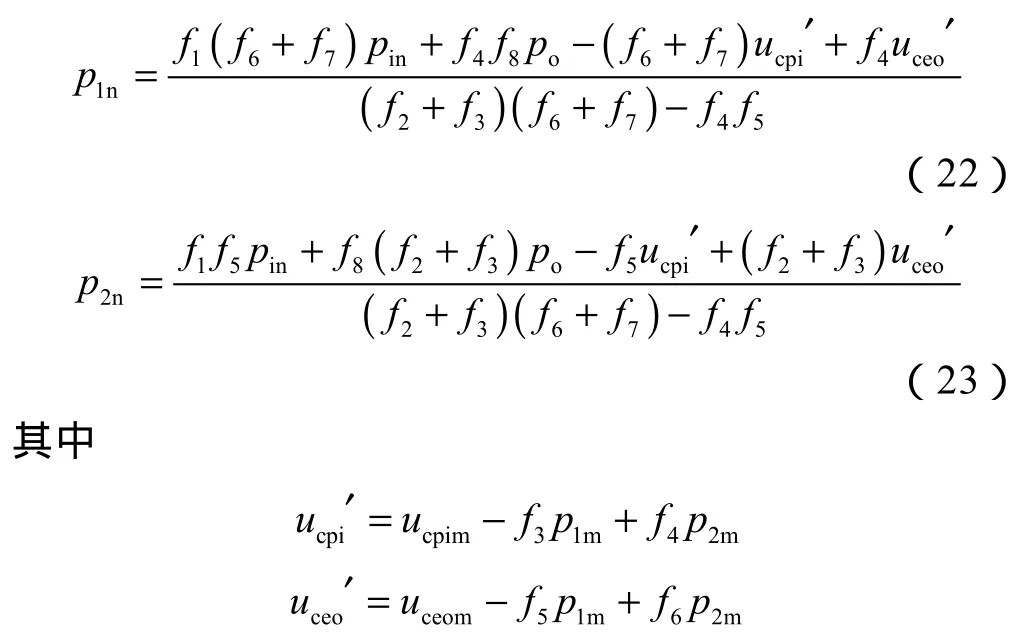
为使界面不发生脱离，水泥环内外壁将分别承受p1n和p2n的拉应力。当实际的界面胶结强度小于计算得到的p1n或p2n时将会产生微环隙，反之则界面不发生脱离。

1.3 微环隙大小计算

微环隙可能产生于第一界面或第二界面，取决于该界面胶结强度与界面拉力的关系。本文仅介绍第一界面微环隙大小的计算方法，第二界面微环隙可用类似方法求解，不再赘述。

当第一界面受拉力超过该界面的胶结强度时，发生界面脱离。此后，套管外壁和水泥环内壁的径向位移不再相同，水泥环和井壁围岩是一个整体，套管单独是一个整体；套管外壁和水泥环内壁压力均变为0。

界面脱离后套管仅受内压pin以及外压p1n= 0的作用。套管外壁处的径向位移为：

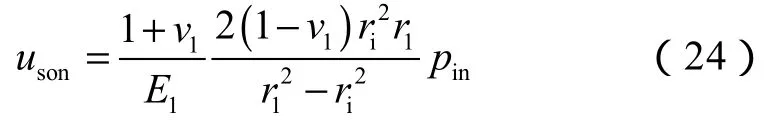
界面脱离后，水泥环内壁压力为0。将p1n=0代入（19）式，得到水泥环内壁径向位移：

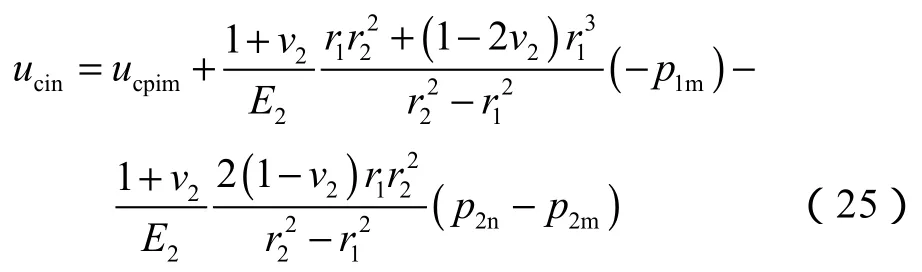
第一界面微环隙的大小dn等于界面脱离后水泥环内壁处位移ucin和套管外壁处位移uson的差值：

将（24）式、（25）式代入（26）式，即可得到第一界面微环隙的大小。其中，p2n可通过水泥环与围岩位移连续条件（ucon= ufin）求解。

2 实例验证

Jackson等[1]在实验室进行了变套管内压条件下微环隙的模拟实验。实验中将Φ127.0 mm套管置于Φ177.8 mm套管中，环空中间充满G级水泥，水泥浆在48.9 ℃、6.9 MPa下养护69 h，实验装置示意图见图2。将套管内压分别加载至14，28，41，55，69 MPa，然后卸载内压并在水泥环上下两端面施加0.69 MPa的压差，检测组合体在不同内压下的气窜程度，从而判断微环隙的产生与发展。

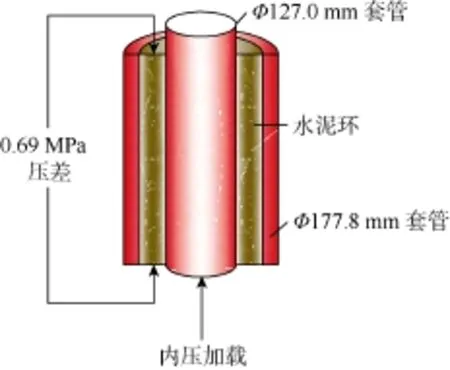
图2 Jackson实验装置示意图

实验结果显示：在内压从0升高直至69 MPa的全过程中，未检测到环间气窜，说明内压的加载未导致组合体密封失效；当套管内压分别加载至14，28，41 MPa然后卸载至6.9 MPa时，也未检测到气窜；当套管内压加载至55 MPa和69 MPa，然后分别卸载至1.4 MPa和3.3 MPa时，检测到明显气窜，由于此前加载阶段水泥环未发生破坏，Jackson等认为在该压力变化下产生了微环隙[1]。

用本文模型对Jackson实验进行模拟。计算时采用与实验中相同的计算参数（见表1），取水泥石内摩擦角30°，内聚力5.77 MPa（对应屈服强度20 MPa）。

表1 Jackson实验组合体尺寸及力学参数

2.1 加载过程中水泥环塑性区发展

计算不同内压下（0～69 MPa）水泥环弹、塑性边界的大小，结果见图3。

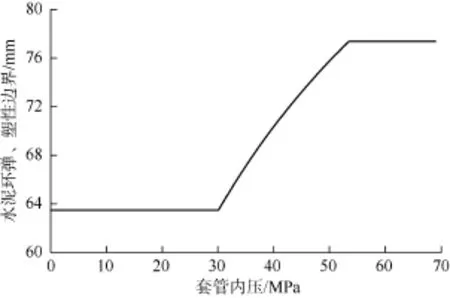
图3 不同加载内压下弹、塑性界面的发展曲线

在加载阶段，当内压从0加载至28 MPa时，水泥环完全处于弹性状态（rp=r1）；当内压加载至30 MPa时，水泥环从内边界开始进入塑性（rp＞r1）；随着套管内压的增加，水泥环进入塑性区的范围也逐渐增大。当内压加载至41 MPa时，弹、塑性边界发展至rp= 71 mm，此时塑性区厚度7.5 mm，当内压升高至53.5 MPa时，rp= r2，水泥环已完全进入塑性状态。若水泥环发生塑性变形，卸压时存在不可恢复的残余应变，而套管产生的弹性形变可以完全恢复，因而有可能在界面处产生微环隙。加载压力越高，水泥环塑性区发展越明显，产生的塑性形变越大。

2.2 水泥环界面接触力的计算

计算内压从0加载至69 MPa时第一界面和第二界面径向应力的大小（压应力为正），结果见图4。在内压从0加载至69 MPa的全过程中，第一界面和第二界面的接触力始终为压应力，此时套管、水泥环以及围岩之间始终受到相互挤压的作用，不会产生微环隙。此结果与实验中在加载阶段未检测到环空气窜的现象相符，证明加载阶段不会产生微环隙。

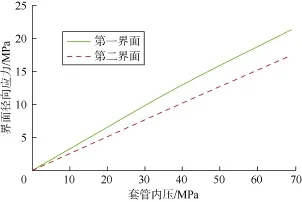
图4 加载阶段界面径向应力的大小

经计算发现，当内压从14 MPa，28 MPa和41 MPa卸载时，第一界面和第二界面的径向应力始终为压应力，故不会产生微环隙。此处着重研究内压从55 MPa和69 MPa卸载时第一界面和第二界面径向应力的大小（压应力为正），结果见图5。第一界面的接触力p1以及第二界面的接触力p2均随套管内压的降低而逐渐降低，且p1降低的速度比p2快。当套管内压力大于4 MPa时，二者均为压应力，不会发生界面脱离；随着内压的进一步降低，p1首先由压应力转变为拉应力（p1≤0），说明在胶结强度相近的情况下，第一界面先产生微环隙。当内压从55 MPa开始卸载时，第一界面处将产生最大约0.7 MPa的拉应力；当内压从69 MPa开始卸载时，第一界面处将产生最大约1.3 MPa的拉应力，若实验中的界面胶结强度小于该值，则会产生微环隙，从而检测到环空气窜。

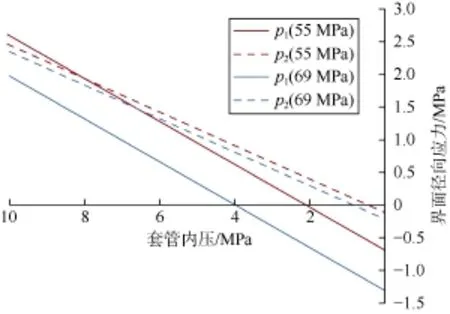
图5 内压从55 MPa和69 MPa卸载时界面径向应力

2.3 微环隙计算

设第一界面、第二界面胶结力均为0.2 MPa（为体现微环隙的产生与发展，选取较小的胶结强度进行计算，以模拟现场施工中固井质量较差的情况）分别计算内压从55 MPa和69 MPa卸载后微环隙大小，此时微环隙产生于第一界面。图6为套管外边界径向位移uso及水泥环内边界径向位移uci随套管内压力变化的曲线，曲线的间距为微环隙大小。当卸载程度较小（套管内压较高）时，uci和uso以相同的速率减小，说明此时水泥环与套管一同收缩，不产生微环隙。当内压减小到一定程度，界面拉力超过胶结强度，界面将被拉开，套管与水泥环发生分离。由于界面拉力的释放，水泥环内壁将突然向外膨胀而套管外壁则突然向内收缩一定距离（图6中虚、实线分离处），此后套管外壁的收缩速率加快，而水泥环内壁的位移不再变化，微环隙随内压降低平稳发展。当内压由55 MPa开始卸载时，压力降低至1.5 MPa后，界面发生分离，最大将产生3.2 µm的微环隙；当内压由69 MPa开始卸载时，压力降低至3.3 MPa后，界面发生分离，最大将产生6 µm的微环隙，导致环空气窜。在实验中，当内压分别卸载至1.4 MPa和3.3 MPa时，检测到气窜。模拟结果与实验结果基本一致，证明了模型的合理性。

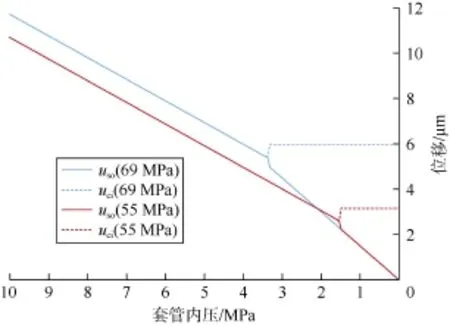
图6 内压从55 MPa和69 MPa卸载时第一界面微环隙

对比内压从55 MPa和69 MPa卸载结果可见：加载阶段的最终压力越高，卸载后产生的微环隙越大；卸载幅度越大，微环隙越大。因此，微环隙的产生是由加载过程和卸载过程两部分共同决定的。加载时内压的大小决定水泥环是否会进入塑性以及塑性状态的发展程度；而卸载时内压降低的幅度则决定水泥环与套管界面处位移差值的大小。

3 结论

建立了套管-水泥环-围岩体系弹塑性力学模型，可对井筒压力变化全过程应力-应变状态进行计算，并分析变内压下第一界面、第二界面微环隙的产生和发展。

微环隙的产生由加载和卸载过程共同决定。加载过程不会产生微环隙，但加载内压的大小决定水泥环塑性变形的程度；而卸载时内压降低将导致界面受拉，从而产生微环隙。

第一界面、第二界面均可能产生微环隙，取决于界面胶结强度与界面拉力的关系。卸载时，第一界面拉力大于第二界面拉力，当两个界面胶结强度接近时，第一界面更容易产生微环隙。

模型可较好地描述室内气窜实验。除常规油气井外，模型还适用于页岩气井水力压裂、储气库井注采等过程的井筒完整性校核，为现场施工提供理论依据。

符号注释：

A——计算参数，用于判断最大、最小主应力；B——与主应力大小相关的中间参数；C——水泥环内聚力，MPa；dn——微环隙，µm；E——组合体某部分的弹性模量，GPa；E1、E2、E3——套管、水泥环、围岩的弹性模量，GPa；f1，f2，f3，f4，f5，f6，f7，f8——中间变量；K——积分常数；p1——套管和水泥环界面处压力（第一界面接触力），MPa；p2——水泥环和围岩界面处压力（第二界面接触力），MPa；p1m——加载终点第一界面处压力，MPa；p2m——加载终点第二界面处压力，MPa；p1n——卸载后第一界面处压力，MPa；p2n——卸载后第二界面处压力，MPa；pi——套管内压力，MPa；pim——套管内最高压力，MPa；pin——卸载后套管内压力，MPa；po——围岩近井地带外边界压力，MPa；pp——水泥环弹塑性界面受力，MPa；r——组合体某处的半径，mm；r1——水泥环内半径，mm；r2——水泥环外半径，mm；ri——套管内半径，mm；ro——井壁围岩外半径，mm；rp——水泥环弹塑性边界，mm；u——组合体某处的位移，µm；ucei——水泥环弹性区内壁的径向位移，µm；uceo——水泥环弹性区外壁的径向位移，µm；uceom——加载阶段水泥环弹性区外壁径向位移，µm；ufi——围岩内壁的径向位移，µm；ufin——卸载后围岩内壁的径向位移，µm；uci——水泥环内边界径向位移，µm；ucin——卸载后水泥环内壁径向位移，µm；ucir——卸载时水泥环内壁径向位移变化量，µm；ucon——卸载后水泥环外壁径向位移，µm；ucp——水泥环塑性区某点的径向位移，µm；ucpi——水泥环塑性区内壁的径向位移，µm；ucpim——加载阶段水泥环塑性区内壁径向位移，µm；ucpo——水泥环塑性区外壁的径向位移，µm；uso——套管外边界的径向位移，µm；uson——卸载后套管外壁的径向位移，µm；σr——径向应力，MPa；σθ——周向应力，MPa；εr——组合体某部分的径向应变；εθ——组合体某部分的周向应变；ν——组合体某部分的泊松比；ν1、v2、v3——套管、水泥环、围岩的泊松比；φ——水泥石内摩擦角，rad。

[1] Jackson P B,Murphey C E.Effect of casing pressure on gas flow through a sheath of set cement[R].SPE 25698-MS,1993.

[2] Goodwin K J,Crook R J.Cement sheath stress failure[R].SPE 20453-PA,1992.

[3] Saint-Marc J,Garnier A,Bois A P.Initial state of stress:The key to achieving long-term cement-sheath integrity[R].SPE 116651-MS,2008.

[4] Gray K E,Podnos E,Becker E.Finite element studies of near-wellbore region during cementing operations:Part I[R].SPE 106998-PA,2009.

[5] Bois A P,Garnier A,Rodot A,et al.How to prevent loss of zonal isolation through a comprehensive analysis of microannulus formation[R].SPE 124719-PA,2011.

[6] 殷有泉,蔡永恩,陈朝伟,等.非均匀地应力场中套管载荷的理论解[J].石油学报,2006,27(4):133-138.Yin Youquan,Cai Yongen,Chen Zhaowei,et al.Theoretical solution of casing loading in non-uniform ground stress field[J].Acta Petrolei Sinica,2006,27(4):133-138.

[7] 万曦超.油气井固井水泥环力学研究[D].成都:西南石油大学,2006.Wan Xichao.Study on cement sheath mechanics of well cementing[D].Chengdu:Southwest Petroleum University,2006.

[8] 陈朝伟,蔡永恩.套管-地层系统套管载荷的弹塑性理论分析[J].石油勘探与开发,2009,36(2):242-246.Chen Zhaowei,Cai Yongen.Study on casing load in a casing-stratum system by elastoplastic theory[J].Petroleum Exploration and Development,2009,36(2):242-246.

[9] 李军,陈勉,柳贡慧,等.套管、水泥环及井壁围岩组合体的弹塑性分析[J].石油学报,2005,26(6):99-103.Li Jun,Chen Mian,Liu Gonghui,et al.Elastic-plastic analysis of casing-concrete sheath-rock combination[J].Acta Petrolei Sinica,2005,26(6):99-103.

[10] 陈慧发,萨里普 A F.弹性与塑性力学[M].北京:中国建筑工业出版社,2004.Chen Huifa,Salip A F.Elasticity and plasticity[M].Beijing:China Architecture &Building Press,2004.

（编辑 郭海莉）

Calculation of micro-annulus size in casing-cement sheath-formation system under continuous internal casing pressure change

Chu Wei1,2,Shen Jiyun1,Yang Yunfei3,Li Yong1,Gao Deli2
(1.Drilling Research Institute,CNPC,Beijing 102206,China;2.China University of Petroleum,Beijing 102249,China;3.Stanford University,Stanford,CA 94305,US)

The change of internal casing pressure could result in the failure of the cement sheath or the occurrence of the micro-annulus at the interface between the cement and the casing,or at the interface between the cement and the formation due to plastic deformation of the cement.In the hope to estimate the size of the micro-annulus,a theoretical model based on Mohr-Coulomb yield criterion which considers the interaction among casing,cement sheath and formation is built.The plastic behavior of the cement sheath and the bonding strength at two interfaces are taken into account.Particularly,the initiation and the development of micro-annulus at two interfaces (casing-cement sheath interface and cement sheath-formation interface) are analyzed.This model is further used to simulate Jackson and Murphey’s experiment,which studied the gas channeling in the annular space.Good agreement is found in general.Results show that both loading and unloading processes contribute to the initiation of the micro-annulus.Loading process may lead the cement sheath into plasticity.The radial stress at the interfaces turns into tensile stress during the unloading process.Micro-annulus could appear at both interfaces if the tensile stress exceeds the corresponding bonding strengths.If the bonding strengths at two interfaces are of similar magnitude,the micro-annulus would be more likely to appear at the casing-cement sheath interface due to its higher tensile stress.This model can be used to evaluate the risk of cement sealing failure,especially during the hydraulic fracturing,and lower the risk of zonal isolation failure.

micro-annulus in casing-cement sheath-formation system;well integrity;elastoplasticity;bonding strength;pressure loading process;pressure unloading process

国家重点基础研究发展计划（973）项目“中国南方海相页岩气高效开发的基础研究”课题3“页岩气水平井钻完井关键基础研究”（2013CB228003）；国家自然科学基金创新研究群体项目（51221003）；中国石油天然气集团公司重大专项“中国石油天然气集团公司重大专项群体项目研究”（2013E-38-05）

TE25

A

1000-0747(2015)03-0379-07

10.11698/PED.2015.03.16

初纬（1988-），男，北京市人，硕士，主要从事固井方面的研究工作。地址：北京市昌平区沙河镇西沙屯桥西中石油科技园A34区块，中国石油集团钻井工程技术研究院，邮政编码：102206。E-mail:791682172@qq.com

联系作者：沈吉云（1984-），男，江苏盐城人，法国路桥研究中心博士，中国石油集团钻井工程技术研究院工程师，主要从事固井方面的研究工作。地址：北京市昌平区沙河镇西沙屯桥西中石油科技园A34区块，中国石油集团钻井工程技术研究院，邮政编码：102206。E-mail:shenjydr@cnpc.com.cn

2014-07-31

2015-04-16