坡面地表填洼量估算方法研究

赵光旭，王全九，2，杨 婷，苏李君

（1.西安理工大学 水利水电学院，西北旱区生态水利工程国家重点实验室培育基地，西安710048；2.西北农林科技大学水土保持研究所，黄土高原土壤侵与旱地农业国家重点实验室，陕西 杨凌712100；3.西安理工大学 理学院，西安710048）

地表糙度特征是研究水文循环［1］、土壤侵蚀［2］的重要影响因素。对于坡耕地［3］，不同的土地利用方式导致土壤下垫面条件发生变化，直接影响地表填洼量、地表径流、土壤入渗［4］、坡面水流特性，以及土壤侵蚀及养分迁移过程［5］。通常用地表糙度反映地表的高低起伏程度，地表糙度越大，填洼量越大［6］。降雨过程中，填洼量影响地表径流的产生，并且改变地表径流方向，是分析地表径流变化特征的重要参数［7］。填洼量与地表糙度之间的关系密切，国内外学者针对填洼量与糙度之间定量化的关系进行了大量的研究。目前地表糙度的测量方法可以分为接触式测量和非接触式测量［8］两种方法。前者主要是利用传统的手段进行地表糙度的测量，主要包括链条法［9］、测针法［10］、尺杆法等。其中链条法适用于野外大面积地表糙度测量，操作简单，测量速度快；测针法只适用于小面积的地表糙度测量；尺杆法也适用大面积测量，原理和测针法类似。随着GIS技术的发展，地表糙度的测量进入到了一个全新的发展阶段，像激光扫描仪［11］和立体摄影法［12］等，称为非接触式测量方法。和传统的测量方法相比，激光扫描仪法和立体摄影法等不仅测量速度快、精度高，而且对地表土壤结构的破坏较小。目前测量地表填洼量的方法有很多，最为常用的方法是薄膜法［13］，利用的是水量平衡的原理；GIS法［14］是利用ArcGIS软件来分析野外微地形，相对来说测量精度较高，但是过程复杂，需要大量专业知识和借助计算机才能进行分析；Kamphorst等对数十种地表糙度指标与地表最大填洼量（MDS）关系研究表明，其中3种地表糙度指标与MDS［15］相关性高，可以作为计算MDS的有效指标，这3种指标分别为随机糙度（RR）、LD×LS和平均上坡凹陷量（MUD）；在微 DEM 条件下，赵龙山等［16］指出，填洼量与坑洼深度和坑洼面积密切相关，其变化规律可用二次抛物线描述。

由于微地形变化受到多种因素的影响，如何合理估算填洼量，以及如何分析填洼量与坡面糙度之间的关系仍需进一步研究。本文通过研究不同几何形状（半圆形、矩形、三角形、梯形及组合）在坡度、坡长、供水流量条件下填洼量的变化过程，将不同尺度、不同形状的地表坑洼概化为不同尺寸的规则几何形状，发展地表填洼量估算方法，为坡面水流计算分析提供简单方法。

1 材料与方法

1.1 试验内容

为了评估填洼量估算方法，在室内进行不同概化微地形形状（半圆形微地形、三角形微地形、梯形微地形、矩形微地形、4种形状组合的微地形）、坡度（5°，10°，15°，20°，25°，30°）、坡长（0.4m，1.2m，1.5m）、上方来水流量（750ml/min，1 778ml/min，2 250ml/min）等条件下的放水试验，同时在野外也进行3个上方来水流量（13.4L/min，19.4L/min，20.3L/min）的坡面放水试验。室内试验和野外试验均采用链条法来测量地面糙度，其计算公式为：

式中：Cr——相应地表任意方向上的地表糙度；L1，L2——链条长度与坡面直线长度。填洼量是通过测定入流量和出流量，依据水量平衡原理计算得出。

1.2 试验系统

室内试验于2014年4—6月在中国科学院水利部水土保持研究所黄土高原土壤侵蚀与旱地农业国家重点实验室进行。试验系统包括试验土槽、供水系统。试验土槽由塑料板制作而成，宽为0.23m，高为0.35m。为了分析坡长影响，长度分别为0.4m，1.2 m和1.5m三种长度。垄沟在坡面均匀排开（其中0.4m长坡面有5个垄沟，1.2m长坡面有10个垄沟，1.5m长坡面有13个垄沟）。在土槽一端连接供水装置，另一端连接集水槽。采用蠕动泵供水，并通过控制供水泵的台数来控制流量。土槽和放水装置放在一个可以调整相应坡度的支架上，研究坡度的影响。野外试验于2014年8月在水保所神木侵蚀与环境试验站展开，供水采用能产生稳定水流的装置，试验所选取坡面的长度为16m，宽度为1m，坡度为10.8°，整个坡面为裸地，有25个垄沟，在坡面均匀排列，垄沟形状为半圆形，其半径为0.15m。室内和野外试验均采用高锰酸钾溶液来测定流速。

1.3 试验过程

室内试验土样选自杨凌农耕土壤，将土样经过风干、碾碎、过筛等基本处理之后，按照容重为1.34 g/cm3，分层（5cm 一层）填装土槽，总装土高度为0.2m。为了便于构筑微地形，上部5cm利用制作的微地形模具控制装填土数量。填土完成之后取出模具，用链条法进行糙度测量。在填好的土槽表面按照模具形状进行覆膜，如图1所示。覆膜之后，调好坡度，进行放水试验。放水试验开始后，首先应精确记录产流时间，待集水槽处有水流出时，采用容量大约为3.5L的小水桶收集径流，每2min接一次水，记录水样体积，收集径流时间为1h。野外试验步骤与室内试验基本相同。

图1 坡面垄沟覆膜前后对比

1.4 填洼量的理论计算公式

本研究将凹凸不平的地表概化为规则的几何形状微地形地表，通过数学方法计算理论填洼量，然后与试验测得的填洼量进行对比，获得相应的修正关系，以便于实际填洼量的估算。图2显示了坡长为0.4m时概化的各微地形的纵剖面图。由于坡度变化，微地形所形成的填洼量不能按照水平情况下的形状进行填洼量估算，需将微地形分割成规则图形进行计算。

以半圆形微地形为例，分析填洼量计算过程。为了便于计算，将半圆形微地形分割成三部分，如图2A所示。

图2 各微地形纵剖面示意图

在给定坡度下，如获得一个坑洼中填洼量的横截面积A1，乘以土槽的宽度，就可以求出一个坑洼的填洼量，根据坑洼的个数，就可以求得整个坡面的填洼量。由于A1等于半圆面积减去A2和A3，其中A2为扇形，面积计算公式为：

式中：R——半圆形的半径（m）；θ——坡度（°）；A3为三角形，面积计算公式为：

因此A1表示为：

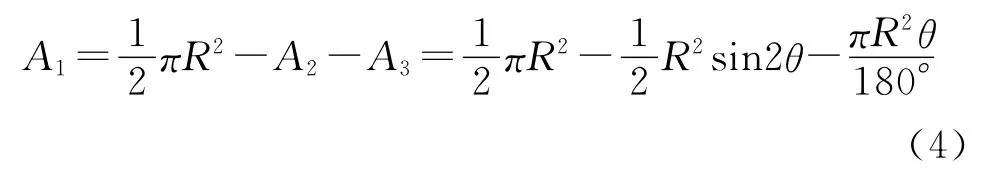
整个坡面理论填洼量计算公式为：

式中：V1——整个坡面的理论填洼量（ml）；l——坡宽（m）；n——半圆形分布个数，其他同上。类似方法推求其他微地形填洼量。

三角形理论填洼量计算公式为：

式中：V2——整个坡面的理论填洼量；a——三角形边长（m）；α——三角形夹角（°）；θ——坡度；l——坡宽；n——三角形坑洼分布个数。

梯形理论填洼量计算公式：

式中：V3——整个坡面的理论填洼量；a——梯形的腰长（m）；b——上底边长（m）；α——底边与腰的夹角（°）；θ——坡度。

矩形理论填洼量计算公式：

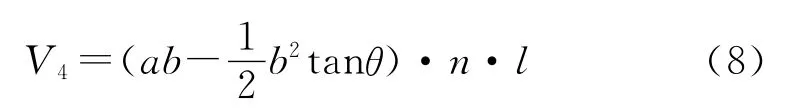
式中：V4——整个坡面的理论填洼量；a——矩形的宽（m）；b——矩形的长（m）；θ——坡度。

对于组合形式的微地形，由4种不同的形状组成，如图2E所示，各形状填洼量的计算利用上述4种形状填洼量的计算公式求得，然后根据各形状坑洼的个数，即可求得整个坡面的填洼量。在实际估算中，只要知道坡面的宽度l和坡面坑洼的个数n，即可应用上述公式进行计算。

2 结果与分析

上面通过对微地形概化，建立不同形状下地面填洼量计算公式，但在降雨条件下，水流特征受到多种因素的影响，实际填洼量与理论填洼量之间存在差异，因此需要分析各种因素对其造成的影响。

2.1 坡度对填洼量的影响

图3显示了不同坡度条件下5种微地形的理论填洼量和实测填洼量。由图3可知，实测填洼量大于理论填洼量，这是因为理论公式计算的只是静止状态下填洼所能蓄存的水量，是严格按照几何尺寸计算出来的，并没有考虑流过垄宽的水量，而实测填洼量不仅包含填洼所蓄存的水量，还包括在产流过程中由于表面张力的作用，导致水面雍高，使得填洼的水面上升，填洼量增大，再加上垄上的流动水流，必然使得实测填洼量大于理论填洼量。

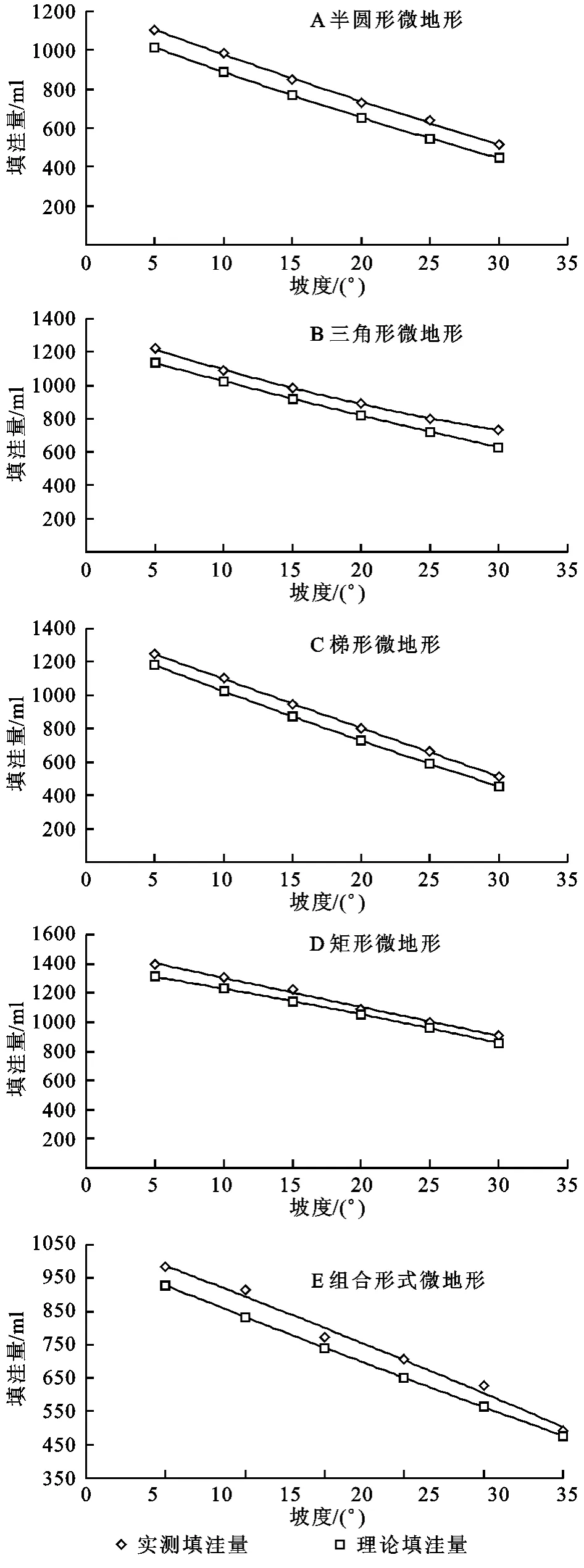
图3 各形状微地形填洼量随坡度的变化关系

2.2 上方来水流量对填洼量的影响

图4分别显示了三角形微地形（A）和半圆形微地形（B）条件下实测填洼量随上方来水流量的变化关系。在下文涉及理论填洼量和实测填洼量的计算式中：理论填洼量用Vthe表示，实测填洼量用Vmea表示。

由图4可以看出，填洼量与流量呈现出良好的线性关系，通过线性函数来拟合，所得结果如下：三角形微地形：

式中：Vmea——实测填洼量；Q——流量（ml/min）。

2.3 坡长对填洼量的影响

图5显示了实测填洼量与坡长的关系。从图5中可以看出实测填洼量随着地表坡长的增加，呈现逐渐增加的趋势，并且表现出良好的线性关系，通过线性函数来拟合，获得的结果如下：

式中：Vmea——实测填洼量（ml）；L——坡长（m），将上述三个方程分别对L进行求导，求得结果为1 951.7，1 735.5，1 503.8，即分别为5°，10°，15°拟合方程的斜率，斜率依次减小，说明当地表坡度变大时，随着坡长的增加，地表填洼量增长的幅度降低。

图6显示了单位坡长填洼量随坡长的变化关系，从图中可以看出单位坡长实测填洼量虽然有下降趋势，但并没有随着坡长发生明显的变化。

2.4 理论填洼量与实测填洼量之间关系的修正

由上面分析可知，理论填洼量和实测填洼量之间存在明显差异，但是两者之间的差异存在一定规律。因此，可以依据实测填洼量对理论填洼量进行修正，从而得到能应用于实际的理论计算公式。由于实际地表比较复杂，我们将各种情况进行综合分析，提出综合修正系数。

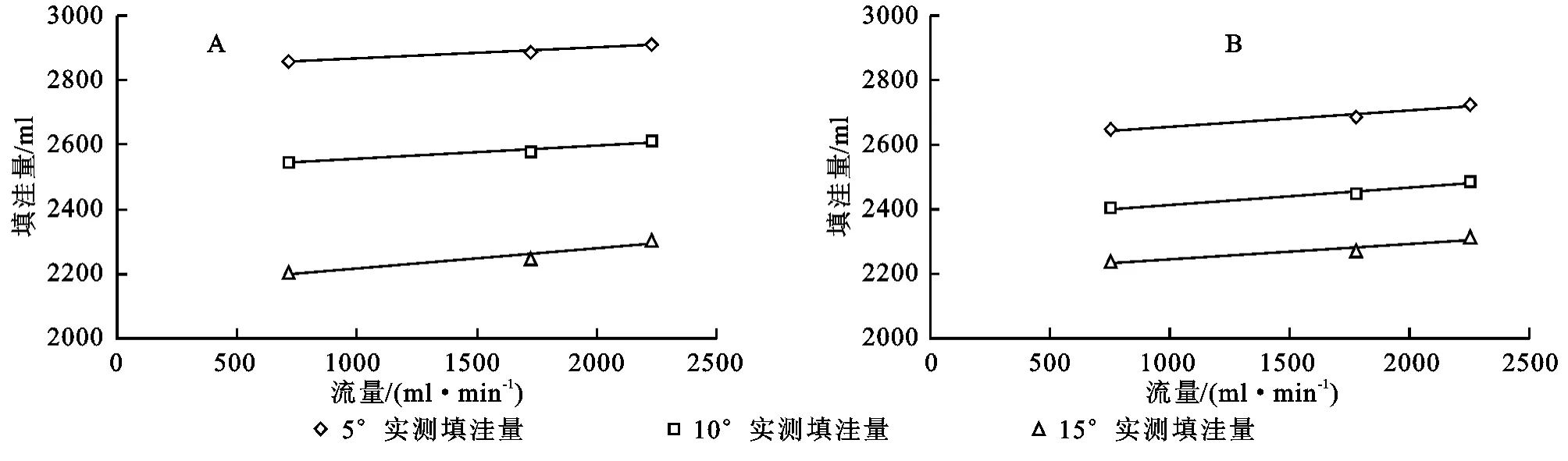
图4 三角形微地形（A）和半圆形微地形（B）实测填洼量随上方来水流量的变化关系

图5 实测填洼量与坡长的关系

图7显示了在不同微地形、坡度、坡长、上方来水流量条件下理论填洼量与实测填洼量的之间的关系，其关系式为：

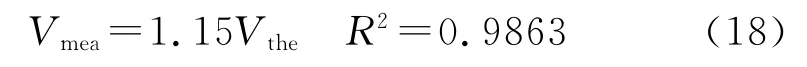
由相关关系来看，两者存在良好线性关系，相对误差在15%左右。

为了进一步评估填洼量计算公式的合理性，进行了野外试验。根据测得的基本数据通过公式（5）计算得到整个坡面的理论填洼量，然后再由修正公式（18）对所求的理论填洼量进行修正，最后与试验得到的实测填洼量进行对比，所获得结果如表1所示。

图6 单位坡长填洼量随坡长的变化情况

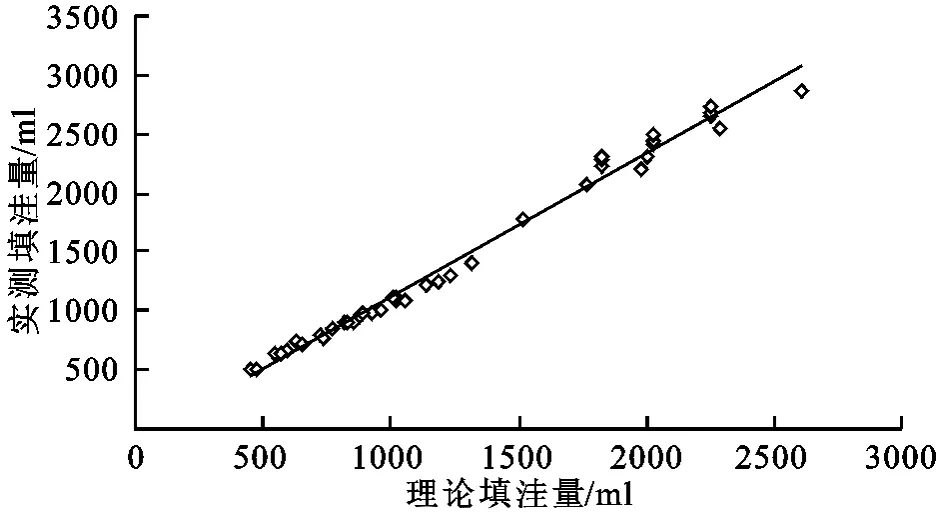
图7 理论填洼量与实测填洼量的修正关系

从表1可知，由理论公式推求的填洼量经过修正后与实测填洼量相差在10%左右，说明理论公式可以用于实际填洼量计算。

2.5 填洼量与地表糙度的关系分析

一般填洼量估算是依据地表糙度进行计算，因此需要分析填洼量与地表糙度间关系。选用单位坡长（长度为1m）半圆形微地形为研究对象，单位坡长上均匀设置8个半圆形坑洼，通过改变其半径来改变地表糙度，通过公式（5）计算在不同地表糙度（0.1，0.2，0.256，0.3，0.313 5）和不同坡度（5°，10°，15°，20°，25°，30°）条件下单位宽度填洼量，计算结果见表2。

由表2可以看出，随着地表糙度增大，填洼量逐渐增大。利用下式对两者关系进行拟合，结果如下：

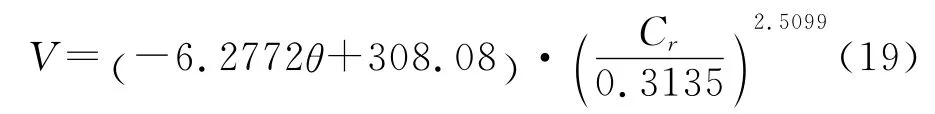
式中：V——填洼量；θ——坡度；Cr——地表糙度，通过公式（19）计算坡度为5°和30°条件下的地表填洼量（拟合值），与通过公式（5）计算得到的填洼量（计算值）进行对比，两者几乎没有差异，拟合效果良好。

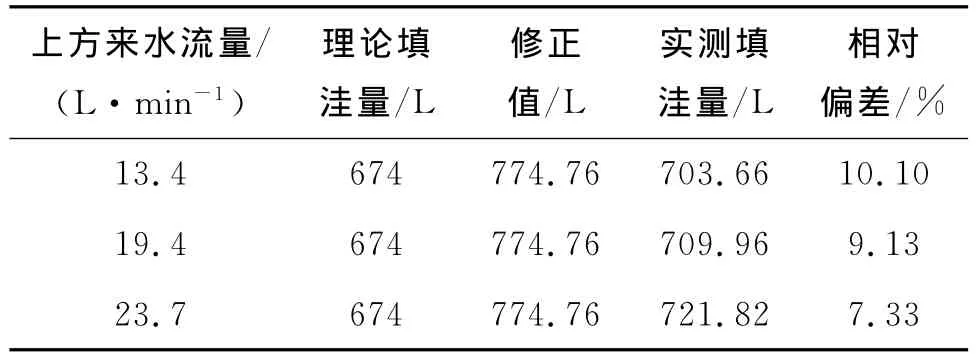
表1 理论计算结果与实测结果对比

表2 不同地表糙度和坡度条件下地表填洼量 ml

3 结论与讨论

（1）半圆形微地形、三角形微地形、梯形微地形、矩形微地形、组合形式微地形的实测填洼量均大于理论填洼量，并且两者随着坡度的增大均减小；填洼量随着流量的增加呈现出增加的趋势，在不同坡度情况下，满足相应的线性增长关系；填洼量随着坡长的增加而增加，当地表坡度逐渐变大时，随着坡长的增加，填洼量增长的幅度降低，单位坡长填洼量随坡长没有明显变化。综合不同微地形、坡度、坡长和上方来水流量等条件所得到的修正系数为1.15，推求的理论公式和修正系数经过野外试验的验证，取得了较好的效果。

填洼量对地表径流的大小有直接影响，这种影响与土壤入渗能力有关。为了获得符合实际情况下的地表填洼量估算方法，我们首先研究了不考虑入渗情况下的地表填洼量估算方法，为考虑入渗情况的填洼量计算提供了研究基础。如估算考虑入渗条件下地面填洼量，应该将土壤入渗能力和降雨或地表水流流量联系起来，进行对比分析，获得不同降雨或水流冲刷情况下地表填洼量。

（2）填洼量与地表糙度关系密切，随着地表糙度增大而逐渐增大，二者表现为乘幂关系。

［1］ 芮孝芳.水文學原理［M］.北京：科学出版社，2004.

［2］ Burwell R，Larson W.Infiltration as influenced by tillageinduced random roughness and pore space［J］.Soil Science Society of America Journal，1969，33（3）：449－452.

［3］ 郑子成，何淑勤，吴发启.坡耕地地表糙度的初探［J］.西北林学院学报，2004，19（1）：39－41.

［4］ 郭建华，吴发启，梁心兰，等.坡耕地地表糙度对降水分配的试验研究［J］.水土保持研究，2008，15（3）：11－14.

［5］ 王全九，王力，李世清.坡地土壤养分迁移与流失影响因素研究进展［J］.西北农林科技大学学报：自然科学版，2007，35（12）：109－114.

［6］ 郭建华.地表糙度与填洼量关系研究［D］.陕西杨凌：西北农林科技大学，2008.

［7］ 郑子成，何淑勤，吴发启.降雨对地表糙度影响的研究［J］.水土保持研究，2003，10（2）：151－154.

［8］ Jester W，Klik A.Soil surface roughness measurement：methods，applicability，and surface representation［J］.Catena，2005，64（2）：174－192.

［9］ Saleh A.Soil roughness measurement：chain method［J］.Journal of Soil and Water Conservation，1993，48（6）：527－529.

［10］ Kuipers H.A relief meter for soil cultivation studies［J］.Neth.J Agric.Sci.，1957，5（4）：255－262.

［11］ KamphorsT E，Jetten V，Gurif J，et al.Predicting depressional storage from soil surface roughness［J］.Soil Science Society of America Journal，2000，64（5）：1749－1758.

［12］ Warner W S.Mapping a three－dimensional soil surface with hand－held35mm photography［J］.Soil and Tillage Research，1995，34（3）：187－197.

［13］ 宋冰，赵龙山.微地形条件下地表填洼量计算方法研究［J］.杨凌职业技术学院学报，2011，10（3）：5－7.

［14］ 赵龙山，张青峰，梁心蓝，等.基于GIS的坡耕地数字高程模型的建立与应用［J］.农业工程学报，2010，26（11）：317－322.

［15］ Hansen B，Schjnning P，Sibbesen E.Roughness indices for estimation of depression storage capacity of tilled soil surfaces［J］.Soil and Tillage Research，1999，52（1）：103－111.

［16］ 赵龙山.黄土坡耕地地表糙度的特征与建模研究［D］.陕西杨凌：西北农林科技大学，2011.