汇管对下游天然气管道速度场影响的数值模拟

谭 欢， 王 淇

（1. 西南石油大学 石油与天然气工程学院， 四川 成都 610500； 2. 西气东输管道公司管道建设项目部， 江苏 镇江 212000）

汇管对下游天然气管道速度场影响的数值模拟

谭 欢1， 王 淇2

（1. 西南石油大学 石油与天然气工程学院， 四川 成都 610500； 2. 西气东输管道公司管道建设项目部， 江苏 镇江 212000）

对几种常见湍流模型的功能及局限性进行比较分析，得到最合适的模型。并利用CFD软件FLUENT对汇管下游DN100的直管道内部流场进行数值模拟，得到合理的速度场分布。通过对比三种不同工况下的速度场分布，得到三种特定工况条件下，汇管下游的天然气速度恢复均匀稳定时的长度范围，如当Q为554 m3/h时，圆管内气体流动充分发展为稳定状态时的最短管道长度为17D，该长度范围对确定超声波流量计的现场安装位置具有很好的借鉴作用。

汇管下游；FLUENT；湍流模型；速度场

随着现代天然气工业的迅速发展，天然气已经成为一种主力燃料。在天然气的采、运、储、销、用各个环节，其计量的准确性及可靠性对各方的成本、经济效益等有直接关系。对于现场实际计量管道，由于空间的限制，流量计上游不可避免的存在各种工艺设备和管件，如：弯管、汇管，而管道内气体流场分布的稳定性对流量计的计量准确度有很大影响，为了保证计量的准确度，应充分考虑流量计上游各种工艺设备和管件对天然气流态的扰动影响[1-3]。为了降低研究的周期和成本，本文利用CFD FLUENT软件对流量计上游、汇管下游的直管段进行三维建模和数值仿真，观察流入流量计的气体速度剖面是否充分发展，通过分析该段气体速度场分布规律，对现场流量计的安装具有很好的借鉴作用。

1 比较湍流模型

自然界中的流体流动状态主要有两种形式，即层流和湍流。湍流是在中、高雷诺数液体流动中观察到的非稳态的、非周期的随机运动，是一种连续介质的流动形态，湍流是最普遍存在的。

然而没有一个通用湍流模型能有效的解决所有湍流问题。为具体问题选择最合适的湍流模型要考虑流体的物理性质、精度等级、可实行的计算资源和仿真模拟所需的时间量等因素，故需要了解各个湍流模型的功能和局限性。对常用湍流模型的功能和局限性进行对比分析如下表1所示。

其中，kε-湍流模型在工程应用中的发展最为成熟，积累的经验最丰富，该模型适用于各向同性的均匀湍流流动，即该湍流模型能很好反映充分发展的管流流动的实际情况。

结合本文具体应用，故采用标准kε-模型对汇管下游管道气体流态进行仿真，并利用FLUENT 14.5进行实例分析。

表1 湍流模型性能分析比较表Table 1 The performance analysis and comparison of turbulence models

2 实例

2.1 模型的建立

2.1.1 物理模型

GB-T 18604-2001规定，超声波流量计的直管段安装要求为：不安装流动调整器，多声道气体超声流量计上游的最短直管段长度为10D，下游最短直管段长度为5D，该项要求在上游条件较为理想时成立，为最低要求[4]。本文研究对象为超声流量计上游带汇管时的计量直管段，观察该直管段长度为20D内的速度场分布情况。

采用Pro/E软件对超声波流量计上游带有汇管的计量管段进行三维建模，几何模型如图1所示，其中，坐标原点定义在汇管截面的中心，汇管进口直管道长度为2D，汇管型号为P=6.93 MPa，DN300 ×4400，汇管下游直管道长度为20D。

并将三维模型导入ANSYS-ICEM软件对三维几何模型进行网格划分，总共有1 479 471个单元，252 278个节点。

2.1.2 边界条件

Fluent软件模拟边界条件类型时进口选择“Velocity-inlet”，出口选择自由流出“outflow”，区域wall选择默认边界，且无滑移条件。

管内的流体介质为天然气，其入口端平均流速分别设为V1=19.62、V2=2.51、V3=0.93 m/s，工作温度在12 ℃左右，压力为0.8 MPa，气体密度为0.68 kg/m3，运动粘性系数 1.603×10-5m2/s。音速为a=340.3 m/s。

图1 汇管及其下游直管段几何模型Fig.1 The geometry model of manifold and its downstream straight pipe.

由进口流速求得对应的马赫数分别为Ma=0.058、0.007 4、0.002 7，Ma值均小于0.3，故流动为不可压缩流体。由雷诺数计算公式求得Re分别为Re=122 396、15 658、5 801，故气体的流动状态均为湍流。

2.1.3 数学模型

流体流动过程遵守物理守恒定律，基本守恒定律有：质量守恒定律、动量守恒定律、能量守恒定律；因本文天然气流动为湍流，故还需要遵守湍流输运方程。对以上物理守恒定律进行数学描述就得到了控制方程，三维压力-速度耦合问题的模型方程如下：

式中(1),(2),(3)式为x方向、y方向和z方向的动量方程，第(4)式为连续性方程。软件采用交错网格方法和SIMPLE算法求解该方程组。

2.2 数值模拟结果及分析

为保证流经汇管的天然气计量的准确性，流量计在汇管下游直管段中的安装位置应无明显流速不均性的影响，故对汇管下游的气体流动状况进行分析讨论是本文的主要目的。

为了便于分析研究，对汇管下游不同长度的管道截面流场进行分析比较，一般来说，在管流流动中，轴线上的湍流发展状态可以代表整个截面上流动的发展状态[5]，故对下游管道轴线上的速度值及湍流强度随管长L的变化情况进行分析，进而得到汇管下游的天然气流场恢复均匀稳定时的距离长度范围。

2.2.1 下游直管道内部速度分布随工况变化规律

图2为流量分别为105.14、283.92、554 m3/h时下游直管道内部速度场分布图，从图2中可以看出：

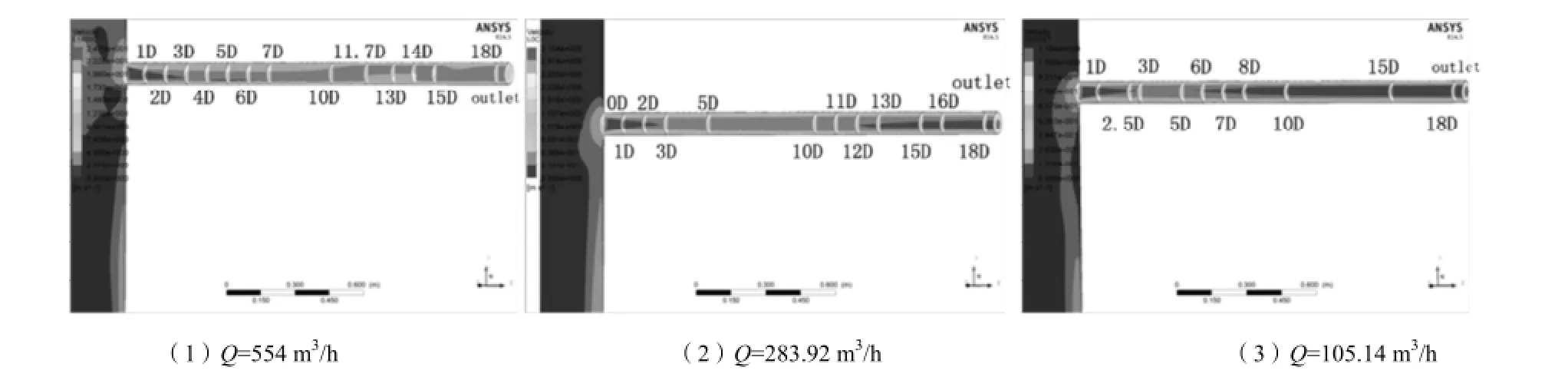
图2 汇管下游直管道内部速度场分布在不同输量下的局部放大图Fig.2 The velocity field distribution inside the downstream straight pipe under different work condition

a.三种不同工况条件下，流场内速度主要分布在汇管与下游管道交汇处，且此处的速度值均发生较大突变，其湍动能和湍流强度均为整个流场内最大，相比汇管内则基本比较稳定,这是因为汇管与下游直管段交汇处因结构突变产生涡旋、引发强烈湍流[5]；

b.当Q=554 m3/h时汇管与下游直管道交汇处的速度值能达到24.75 m/s。随着下游直管道长度的增大V有减小的趋势，但减小的趋势很小；汇管下游直管道内部速度值大小分布不均，当L＞17D时，气体流速分布基本趋于稳定且管道中心气体流速稳定在19.8～22.28 m/s范围内；

c.流量为283.92 m3/h时，最大速度值能达到3.194 m/s。下游直管道长度L在0D～3D范围内，圆管中心最大速度值覆盖面积随着L的增大有减小的趋势；当L在3D～12D范围内，圆管中心速度值分布基本稳定在2.555～2.874 m/s范围内；当L＞12D时，圆管中心最大速度值覆盖面积随着L的增大逐渐增大，且增大到16D后最大速度值范围不再变化，速度分布趋于稳定；

d.流量为105.14 m3/h时，下游直管道内的速度分布情况同图2（2）相似，圆管中心的最大速度值覆盖范围先减小后增大，但圆管中心速度值分布趋于稳定不变的直管道长度范围是3～5.5D，比图2（2）的管道长度范围要小些，当L增加到10D后最大速度值范围不再增加，速度分布趋于稳定。

可以看出，下游直管道管长L和入口处的气体流速值V（表征入口处的扰动强度）决定了下游直管道内部流动状态。

2.2.2 下游直管道内部速度场分布随L变化规律

当速度分布在流动方向上不再发生变化时，此时流动处于充分发展状态，故要分析汇管下游气体流动的充分发展状态，下文对流量分别为554、283.92、105.14 m3/h时，不同管道长度的YZ截面处内部速度场分布图，以及湍流强度、速度值随着L变化的曲线图进行分析比较。

a.图3（1）可以看出，最大速度值并未分布在圆管中心附近，圆管内气体分布出现明显二次流。

图3 汇管下游直管道各截面速度云图Fig.3 The velocity contours of manifold downstream straight pipe cross-section.

具体的，当L=0D、L=13D截面时，管道上部速度值较大，L从1D～10D时管道下部速度值较大，L从10D～15D时管道中心最大速度值的范围呈顺时针方向变化，可看出汇管下游L从0D～15D范围内有明显的二次流出现，该段气体速度振荡无规律分布；当L ＞17D时，速度的最大值出现在管道的中心位置且速度场分布基本呈同心圆，此段管道内部气体速度呈较均匀分布的趋势。

b.图3（2）可以看出，最大速度值集中分布在圆管中心附近，且L ＞16D时速度的最大值出现在管道的中心位置且速度场分布呈同心圆；随着下游直管段长度的增加，沿壁面的气体流速与管道中心气体流速的相差值呈现先变小后变大的趋势；

具体的，当下游直管段长度L从0D到3D范围内相差值由大变小，且速度最大值出现在管道中心呈椭圆型，这是因为受到汇管上下游气体的压力差，此段气体速度振荡无规律分布；L从3D到11D范围内相差值基本稳定不变，此段气体流态呈平稳均匀分布的趋势；L从12D到15D范围内气体速度相差值由小变大，且较大速度值在圆管中心覆盖范围呈逐渐增大的趋势；当L从16D到出口范围内速度场分布呈同心圆，不受二次流作用的影响，即此段气体速度的分布规律几乎趋于稳定，在16D后安装流量计是比较合理的，且气体到达出口处时管道中心气体流速值稳定在2.874～3.194 m/s范围内。

c.图3（3）可以看出，最大速度值集中分布在圆管中心附近，且L＞10D时速度的最大值出现在管道的中心位置且速度场分布呈同心圆；结合图2得，随着下游直管段长度的增加，沿壁面的气体流速与管道中心气体流速的相差值呈现先变小后变大的趋势。

具体的，下游直管段长度L在0D～3D范围内，圆管中心最大速度值覆盖面积随着L的增大有减小的趋势，且速度最大值出现在管道中心呈椭圆型，这是因为受到汇管上下游气体的压力差，此段气体振荡无规律分布，最大速度值达到1.184 m/s；当L在3D～5.5D范围内，圆管中心速度值分布基本稳定在0.9211～1.053 m/s范围内；当L在5.5D～10D范围，圆管中心最大速度值覆盖面积随着L的增大逐渐增大；当L从10D后最大速度值范围不再增加，速度场分布呈同心圆，不受二次流作用的影响，即此段气体速度的分布规律几乎趋于稳定，在10D后安装流量计是比较合理的，且气体到达出口处时管道中心气体流速值稳定在1.184～1.066 m/s范围内。

从图4可以看出：轴线上的湍流强度随着L的增大有减小的趋势。

(1)图4(1)中，汇管与下游直管道交汇处（即L=0D）湍流强度最大为8%，此处有较强的脉动流；L在0D～6D范围内湍流强度的减小趋势较大；从6D以后湍流强度减小的趋势很小，从6D到16D，湍流强度基本稳定在1%～3%范围内；当L从16D后，湍流强度均小于1%，处于低湍流状态，无脉动流。

图4 湍流强度/速度值随L变化曲线图Fig.4 The curve of turbulence intensity and velocity magnitude changing with the L

看出当输送流量值为554 m3/h时，使得汇管下游气体处于较稳定的、无脉动流的充分发展湍流状态所需直管道长度值大概为17D。

（2）图4（2）中，L=0D处湍流强度最大为0.75%；L在0D～6D范围内湍流强度的减小趋势较大；从6D以后湍流强度减小的趋势很小，从6D后到出口，湍流强度基本稳定在0.1%～0.3%范围内，整个汇管下游直管道内部气体流态均处于较低湍流状态。

可以看出当输送工况流量值大概为283 m3/h时，使得汇管下游气体处于较稳定的充分发展湍流状态所需直管道长度值大概为15D。

（3）图4（3）中，L=0D处湍流强度最大为0.35%；L在0D～6D范围内湍流强度的减小趋势较大；从6D以后湍流强度减小的趋势很小，从6D后到出口，湍流强度基本稳定在0.05%～0.1%范围内，整个汇管下游直管道内部气体流态均处于处于较低湍流状态。

可以看出当输送工况流量值大概为100 m3/h时，使得汇管下游气体处于较稳定的充分发展湍流状态所需直管道长度值大概为10D。

综合本节分析可以看出：

（1）汇管下游直管道内部的气体流态的最大速度值集中分布在圆管中心附近；

（2）随着输送流量值的增大，要使得气体速度分布在流动方向上趋于充分发展所需的下游直管道长度L跟着增大，与前面2.2.1节的结论相同。

4 结 论

（1）三种不同工况条件下，流场内速度主要分布在汇管与下游管道交汇处，且此处的速度值均发生较大突变，其湍动能和湍流强度均为整个流场内最大。

（2）汇管下游直管道内部的气体流态的最大速度值集中分布在圆管中心附近。

（3）随着输送工况流量值的增大，要使得气体速度分布趋于稳定所需要的下游直管道长度L跟着增大，即下游直管道管长L和入口处的气体流速值V（表征入口处的扰动强度）决定了管流截面上是湍流发展状态。

（4）本文只从基本物理量速度V出发对流场进行分析，但反映流场的基本物理量的种类有很多，如压力P、温度T等，在今后的研究工作中，还要进一步将各个物理量相结合来对汇管下游直管道内部介质流场进行分析研究。

［1］ 阎明 . 高精度微功耗时差法超声流量计的设计[D].大连：大连理工大学，2007:1-5.

［2］ 丁凤林，李宗良. 小管径高精度超声流量计设计[J].空间控制技术与应用，2011, 37(2)：28-32.

［3］ 吴志敏，苏满红.时差法超声流量计流速修正系数的数值模拟[J].工业计量，2008,18(4)：1-4.

［4］ GB/T18604-2001. 用气体超声流量计测量天然气流量[S].

［5］ 张宇，栾江峰，张斯亮.基于FLUENT的压力管道内部流场分析[J].当代化工，2014,43(6):1106-1108．

［6］ 李小仨.分支元件结构与湍流场规律仿真研究[D]. 哈尔滨:哈尔滨工程大学，2012,55-57.

［7］ 邱立杰，张国福，赫明.基于FLUENT的弯管内部流场的数值模拟[J].辽宁石油化工大学学报，2013,33(1):48-52.

Numerical Simulation of Manifold’s Effect on the Velocity Field of Gas Pipeline Downstream

TAN Huan1, WANG Qi2
（1. Petroleum and Gas Engineering College, Southwest Petroleum University, Sichuan Chengdu 610500，China；2. PetroChina West East Gas Pipeline Company, Jiangsu Zhengjiang 212000，China）

By comparative analysis of the functions and limitations of several common turbulence models, the most suitable model was obtained. The velocity field in downstream gas pipe of manifold was numerically simulated by computational fluid dynamics software FLUENT, reasonable velocity field distribution was obtained. By comparing the velocity field distribution of three different operating conditions, the length range of downstream piping which make velocity field restore stability was obtained, for instance, when Q=554 m3/h, the necessary shortest pipe length is 17D, which could provide the reference for determining the installation position of ultrasonic flowmeter.

Downstream of the manifold; FLUENT; Turbulence model; Velocity field

TE 832

A

： 1671-0460（2015）01-0215-06

2014-11-06

谭欢（1900-），女，四川成都人，硕士研究生，2015年毕业于西南石油大学油气储运工程，研究方向：从事油气储运完整性分析以及仿真工作。E-mail：258282935@qq.com。