基于有限元分析的动车组牵引电机转子断条故障特性分析

李永新，葛兴来

（西南交通大学电气工程学院，成都610031）

基于有限元分析的动车组牵引电机转子断条故障特性分析

李永新，葛兴来

（西南交通大学电气工程学院，成都610031）

以CRH2型动车组的牵引电机为例，定义了电机转子非对称运行时的电磁场计算模型。基于数值分析的基本原理，利用有限元分析软件Jmag，对牵引电机故障前后的磁场、导条电流进行了计算，并分析了转子断条对电机磁场、气隙磁密、导条电流的影响。同时根据动车组的运行特点，对故障电机在牵引特性曲线上不同工作点下的运行状态进行了仿真，分析了断条故障特征分量随着电机工作点的变化情况，为后续动车组牵引电机断条故障检测技术的研究奠定了基础。

动车组牵引电机；断条故障；电机磁场；特征分量；有限元方法

引言

随着高速铁路在我国的普及，动车组的安全运行受到越来越多的关注。如何保障列车安全可靠地运行成为近期的研究热点和难点。牵引电机作为动车组关键部件之一，研究其故障辨识具有重要意义。动车组中的异步牵引电机与工频异步电机相比在设计思想和运行特性等方面有很大区别［1］，主要表现在：（1）逆变器的输出电压中，除基波外还含有一定的高次谐波；（2）工频电机只工作在50 Hz附近，其运行工况、电压、功率已知，而动车组中的牵引电机采用闭环控制，并按照特定的牵引特性曲线运行，电机的供电电压、供电频率、电机转差率都将随电机工作点的变化而变化；（3）逆变器供电的牵引电机的空间比工频电机紧张，因而电磁参数取得较高。

电机是一个多变量、非线性、强耦合的系统，内部的电磁关系极为复杂，转子断条故障发生后，分析难度进一步加大。有限元方法是公认的分析电机最有效的方法。近年来，研究人员基于有限元法对鼠笼电机断条故障进行了大量的研究［2-7］，研究主要集中在两类：一是研究断条故障对电机性能的影响。文献［8-9］指出断条的相对位置对电机定子电流和启动转矩具有较大影响，而对电机的温升影响较小，电机温升主要受电机断条根数的影响。二是断条故障特征量分量的研究。文献［10-14］指出可以利用电机定子电流边频分量、电机脉动转矩和气隙磁密谐波来对断条故障进行诊断。鉴于动车组牵引电机独特的设计思想和运行方式，研究其故障状态对于电机故障识别具有重要意义。

本文以CRH2型动车组上的异步牵引电机为对象，运用有限元方法分析了断条对电机磁场和导条电流的影响。同时本文仿真分析了断条故障发生后，电机脉动转矩和定子电流边频分量在动车组各个工作点下的变化。

1 磁场分析基础

1.1 假设条件

在电机电磁场求解过程中，为了简化计算分析，作如下假设：

（1）铁心轴向有效长度内的电磁场按二维场来处理，样机计算模型中定子外边界的漏磁可以忽略不计；

（2）不考虑温度对电机参数的影响，绕组端部的漏磁忽略不计；

（3）由于电源频率较低，忽略位移电流的影响；

（4）转子导条与叠片铁心之间绝缘良好，即转子与导条间无直接的电接触，无横向电流。

1.2 电磁场基本方程

本文采用二维电磁场分析模型，认为矢量磁位A只有轴向分量，另外不考虑涡流对定子线圈及铁芯的影响，则电磁场求解方程可表示为

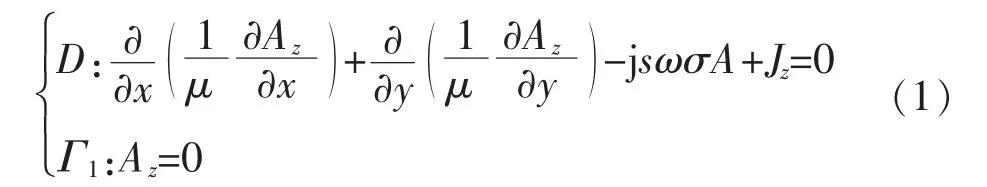
式中：D为求解域；Γ1为定子铁心外圆和转子铁心内圆（第一类边界）；Jz为外加轴向电流密度；σ为电导率；Az为矢量磁位；μ为相对磁导率。

1.3 电机模型介绍

本文以CRH2型动车组的牵引电机为例进行仿真分析，该电机的主要参数如表1所示。

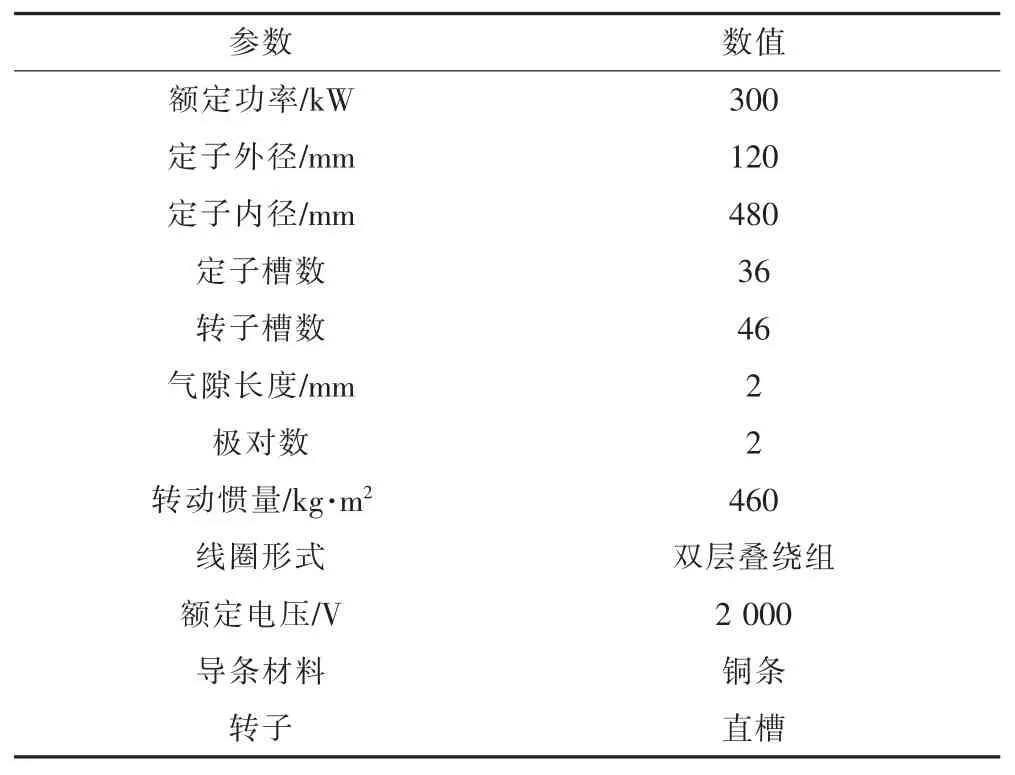
表1 样机参数Tab.1 Parameters of prototype

2 转子断条对电机影响分析

为了分析断条故障对电机的影响，本文根据电机的几何尺寸和电磁参数，在Jmag软件中建立了2D有限元电磁暂态分析模型。

电机正常运行时，磁场对称。为了减少计算节点数，加快计算速度，本文取1/2电机模型进行电磁分析。因而，在进行断条故障仿真时，只能设置偶数根导条在对应位置下故障。本文进行了2根断条和4根断条故障仿真。对鼠笼导条按顺序编号，2根断条故障的断条号为23和46号，4根断条故障的断条号为22、23、45和46号。由于该电机转动惯量较大，断条引起的转矩脉动对电机转速的影响较小，因此可以设定恒定转速进行仿真。为了使分析简单、减小仿真的复杂性，本文采用正弦电压源供电。

2.1 对电机磁场分布的影响

在电机的某工作点下，对转子正常、转子2根断条及4根断条的3种电机分别进行磁场分析。某时刻电机磁密分布、磁力线分布如图1所示。根据电机磁场的对称性，本文使用了软件的镜像功能，呈现出电机全域的计算结果，图中白色导条表示断裂的导条。由图可知，断条故障使得电机磁场呈现出不对称性，并且这种不对称性随着断条根数的增多而增大。磁场的不对称将引起电机在定子轭部和断条周围的齿部发生磁饱和现象。

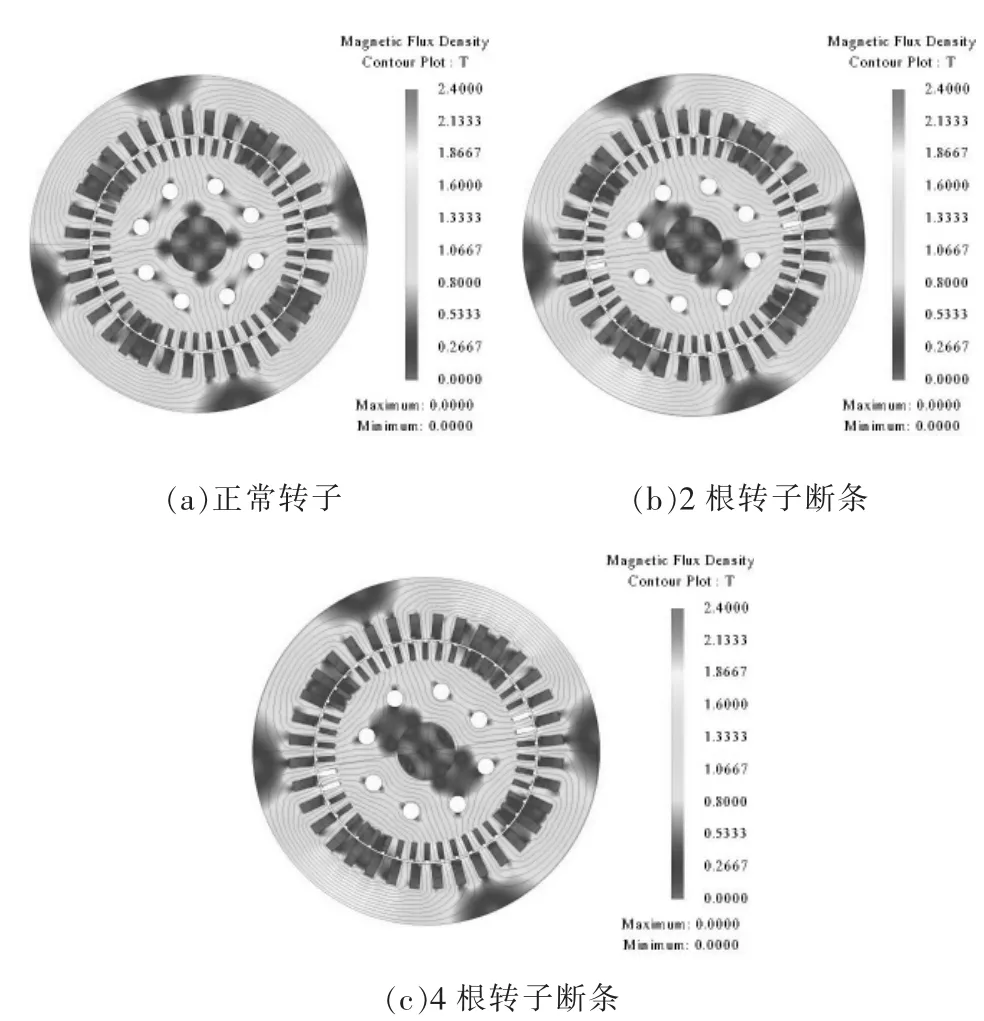
图1 样机不同故障状态下的磁通密分布Fig.1 Magnetic flux density distribution of prototype with different faults

2.2 对电机气隙磁密的影响

电机发生转子断条故障后，磁场分布将不再对称，因而气隙磁密也将随之发生改变。图2为某时刻转子正常、2根断条、4根断条下3种情况的电机气隙磁密圆周分布。

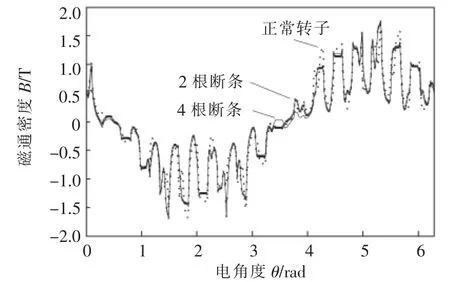
图2 样机气隙磁密径向分量Fig.2 Radial components of air-gap flux density

对电机故障前后的气隙磁通密度进行频谱分析，结果如图3所示。理论上正常电机气隙磁密中仅存在基波和奇次谐波，但由于定转子相对位置的不对称性，正常电机中也存在一定的偶次谐波，并且这些谐波难以被计算［12］。断条故障发生后，气隙中除了正向旋转的磁动势外，还存在反向旋转的磁动势，这就使得电机气隙磁通密度随时间脉动，并使偶次谐波含量增大。由图3可知，随着断条根数的增多，气隙磁通密度中2次谐波含量明显增大。

图3 气隙磁密谐波分量故障前后变化规律Fig.3 Variation of harmonics in air-gap flux density before and after fault

2.3 机定转子电流的影响

对于转子正常的鼠笼电机，因其结构对称，同极性不同极面下对应位置的导条电流大小相等、方向相同。断条故障发生后，导条中电流分布将不再对称，电流大小、相位都发生变化。随着断条数目的增多，导条中电流的不对称性明显增强。图4表示断条前后转子导条中电流基波幅值变化情况。由图可见：与断条位置相邻的导条，其电流基波幅值增大，远离断条位置的导条电流基波幅值减小。断条根数越多，导条电流的不对称性越明显。

图4 导条电流基波幅值分布Fig.4 Fundamental amplitude of bars currents

3 不同工作点下的故障特征量

3.1 动车组牵引电机的工作方式

在实际工作时，动车组按照牵引特性曲线运行。其牵引过程可分为3个调节区：启动加速区、恒定功率输出Ⅰ区和恒定功率输出Ⅱ区。在起动加速区，电机采用准恒转矩、恒磁通控制，供电电压与供电频率成正比增大。此调节区内，电机转矩与转差频率近似成正比。当动车组工作在恒功率输出Ⅰ区时，电机采用恒功率、恒磁通控制。此时供电电压增加，转差频率下降，转矩随着转速增大呈反比规律减小。当动车组工作在恒功率输出Ⅱ区时，电机采用恒功率、弱磁控制。此时电机供电电压保持恒定，转速增大，电机转矩按反比规律减小。

电机的输出转矩Te可以根据动车组轮轨牵引力F计算，即

式中：a为齿轮传动比；d为车轮直径；ηGear为传动效率；N为动车组牵引电机台数。

电机的转速n可以根据动车组运行速度v计算得到，即

式中，np为电机极对数。

本文根据动车组的牵引特性曲线，利用式（2）和式（3）计算出该电机的牵引特性。当转速低于2 456 r/min时，电机工作在启动加速区；当转速介于2 456～3 439 r/min时，电机工作在恒功率输出Ⅰ区；当转速大于3 439 r/min时，电机工作在恒功率输出Ⅱ区。该电机的牵引特性曲线如图5所示。

图5 样机牵引特性曲线Fig.5 Traction curves of prototype motor

在不同的工作点下，由于运行参数的不同，电机故障特征分量的大小也将不同。为了研究电机在全速域内故障特征分量的变化规律，本文选择了8个工作点进行分析。仿真了2根断条故障下，脉动转矩和定子电流边频分量在电机不同工作点的变化情况。仿真工作点在图5中用黑点标注，样机的运行参数如表2所示。

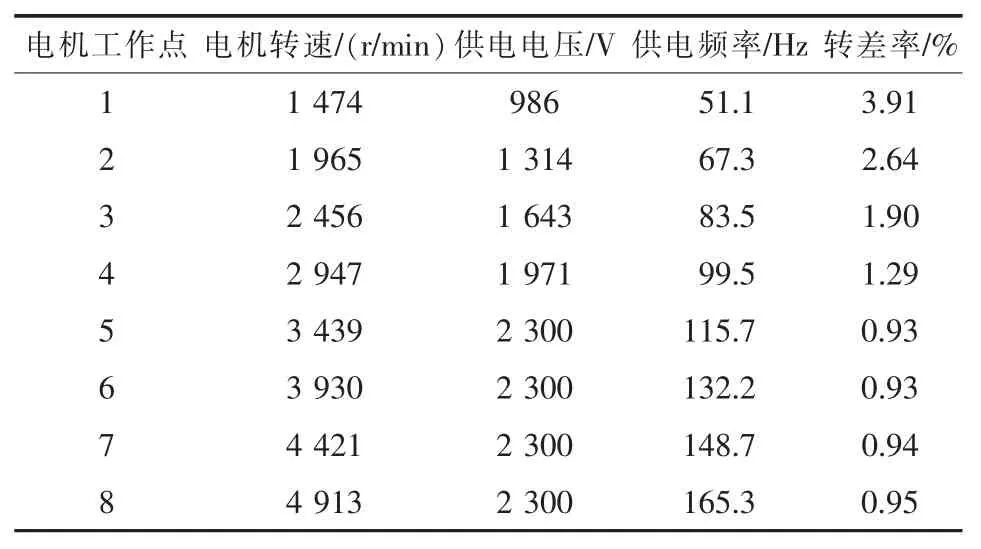
表2 样机的运行参数Tab.2 Operation parameters of prototype motor

3.2 不同工作点下的脉动转矩

对于正常工作的电机，正向旋转的磁场与转子电流相互作用产生稳定的输出转矩。断条故障发生后，气隙中将产生一个反向的旋转磁场，该反向的旋转磁场与导条电流相互作用产生1个以2倍转差频率脉动的转矩，并叠加到稳定输出转矩上［10］。该脉动转矩会增大电机的振动与噪声，其值可以通过相关方法利用电机转矩数据计算，并作为断条故障的判断依据［13］。图6为2根断条的电机在工作点3、工作点5和工作点7下的电磁转矩波形。

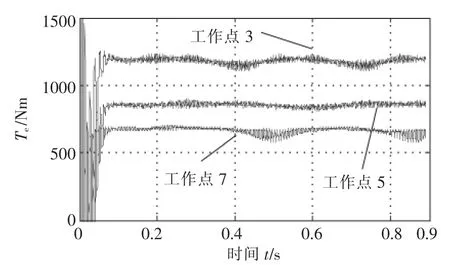
图6 在不同工作点下故障电机的转矩波形Fig.6 Torque of two-broken-bar prototype at different work points

对故障电机的输出转矩进行频谱分析，可知输出转矩中含有一定的2倍转差频率的脉动转矩。该脉动转矩幅值随着电机工作点的不同而发生变化，如图7所示。在动车组的启动加速区和动车组的恒功率输出Ⅰ区，脉动转矩随着电机转速的增加而减小；在恒功率输出Ⅱ区，故障电机脉动转矩随着电机转速的增加而增大。恒功率输出Ⅰ区与恒功率输出Ⅱ区的临界点处，脉动转矩最小。

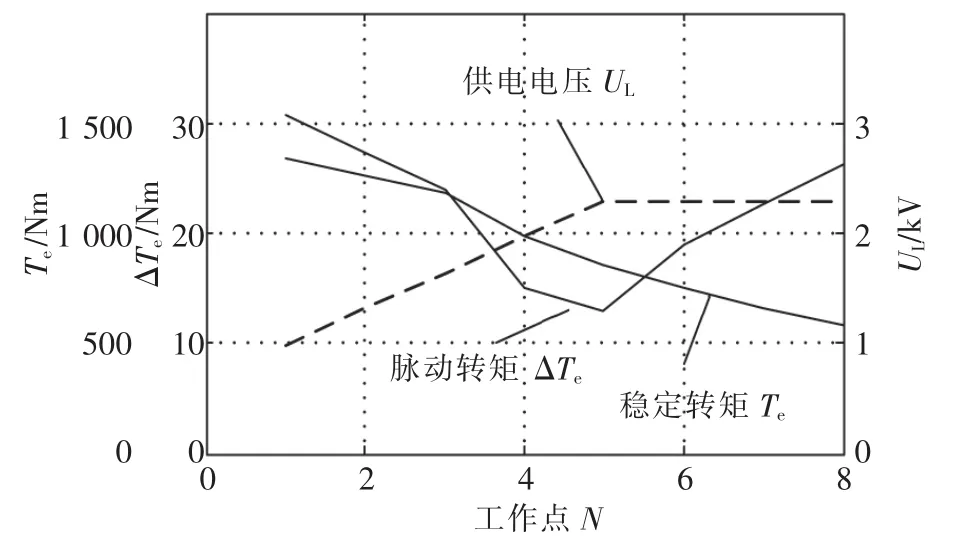
图7 故障电机在不同工作点的脉动转矩Fig.7 Pulsating torque of two-broken-bar prototype at different work points

3.3 不同工作点下的定子电流边频分量

文献［14-15］指出，鼠笼电机发生转子断条故障后，定子电流中将会出现一系列附加特征分量，尤其是定子电流中频率为（1±2s）f1的边频分量常常被用来检测电机断条故障。通过对单相电流信号进行傅里叶变换，即可提取出故障特征量。故障电机在工作点5下运行时，定子A相电流波形如图8所示。

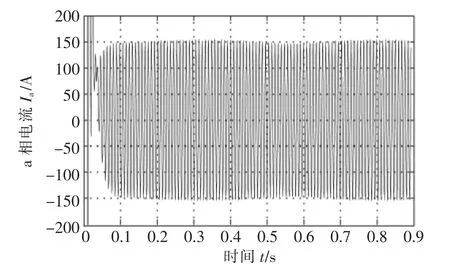
图8 故障电机在工作点5下运行的A相电流Fig.8 Current of phase A for two-broken-bar prototype at work point 5

然而在进行信号处理时，由于转子断条的特征频率fbb与基频f1非常接近，特征分量极易被基频分量的旁瓣“湮没”。再加上动车组实际运行时，电机的转差频率是变化的，从而使得转子断条的特征频率不断变化。直接采用频谱分析的方法很难准确地提取出边频分量。

基于此，人们试图将断条故障特征频率分量2sf1从原始电流信号中“剥离”出来，从而减少甚至免除基频信号的湮没影响。基于扩展Park矢量的诊断方法便是其中较为有效的一种，对故障电机三相电流进行Park变换，根据Park矢量模平方函数判断电机是否故障［16］。在Is的频谱中主要包含电流基波分量对应的直流分量和断条故障对应的频率为2sf1的的交流分量Is2sf。根据Is2sf的大小判断电机是否发生断条故障及故障的严重程度。故障电机运行在工作点3的Is波形如图9所示。

图9 故障电机三相电流Is（t）信号波形Fig.9 Waveform of three-phase currents Is（t）signal for two-broken-bar prototype

对不同工作点下故障电机的Is信号进行频谱分析，可得到各个工作点下Is信号的2倍转差频率（2sf1）的交流分量Is2fs幅值变化如图10所示。由图可知，该交流分量与脉动转矩有类似的性质，即在启动加速区和恒功率输出Ⅰ区，交流分量随着电机转速的增加而减小；在恒功率输出Ⅱ区，交流分量随着电机转速的增加而增加。交流分量在恒功率输出Ⅰ区和恒功率输出Ⅱ区的临界点有最小值。

图10 不同工作点下Is的2sf1交流分量Fig.10 2sf1components of Isat different work points

4 结论

本文基于时步有限元法，研究了转子断条故障对电机磁场、导条电流的影响。同时针对动车组牵引电机独特的运行方式，研究了不同工作点下电机断条故障特征量。

（1）转子断条后，电机磁场将发生畸变，磁场的对称性被打破，畸变使电机出现严重的磁饱和现象。同时，气隙磁密的2次谐波含量增大，因此可以将气隙磁通密度的偶次谐波含量作为电机断条故障的诊断依据；

（2）断条故障后，转子导条中的电流将不再对称分布。邻近断条位置的导条电流增大，远离断条位置的导条电流减小。这种不对称性将随着断条数目的增加而增大；

（3）动车组中牵引电机的故障特征分量大小随着电机工作点的不同而不同。脉动转矩和定子电流边频分量有类似的特性，在启动加速区和恒功率输出Ⅰ区随着转速的增大而增大；在恒功率输出Ⅱ区随着转速的增大而减小；在恒功率输出Ⅰ区和恒功率输出Ⅱ区的临界点有最小值。

［1］李益丰，高培庆.逆变器供电的异步牵引电机特性曲线的计算［J］.机车电传动，1997（6）：8-11.Li Yifeng，Gao Peiqing.Calculation of the performance curve for inverter-fed asynchronous traction motor［J］.Electric Drive for Locomotives，1997，6：8-11（in Chinese）.

［2］Williamson S，Robinson M J.Calculation of Cage Induction Motor equivalent Circuit Parameters Using Finite Elements［C］.IEE Proceedings Electric Power Applications，1991，138（5）：264-276.

［3］Williamson S，Lloyd M R.Cage rotor heating at standstill［J］.IEEE Proceedings Electric Power Applications，1987，134（6）：325-332.

［4］Bentounsi A，Nicolas A.On line diagnosis of defaults on squirrel cage motors using FEM［J］.IEEE Transactions on Magnetics，1998，34（5）：3511-3514.

［5］Kim C E，Jung Y B，Yoon S B，et al.The fault diagnosis of rotor bars in squirrel cage induction motors by time-stepping finite element method［J］.IEEE Transactions on Magnetics，1997，33（2）：2131-2134.

［6］Yeh C C，Mirafzal B，Povinelli R J，et al.A condition monitoring vector database approach for broken bar fault diag-nostics of induction machines［C］.IEEE International Conference on Electric Machines and Drives，2005：29-34.

［7］Mirafzal B，Demerdash N A O.Induction Machine Broken-Bar Fault Diagnosis Using the Rotor Magnetic Field Space Vector Orientation［C］.Conference Record of the Industry Applications Conference，2003.38th IAS Annual Meeting IEEE，2003，3：1847-1854.

［8］谢颖，李伟力，李守法.异步电动机转子断条故障运行时定转子温度场数值计算与分析［J］.中国电机工程学报，2008，23（10）：33-39.Xie Ying，Li Weili，Li Shoufa.Calculation and analysis of temperature field for induction motors with broken bars fault［J］.Proceedings of the CSEE，2008，23（10）：34-39（in Chinese）.

［9］Xie Y.Performance evaluation and thermal fields analysis of induction motor with broken rotor bars located at different relative positions［J］.IEEE Transactions on Magnetics，2010，46（5）：1243-1250.

［10］Elkasabgy N M，Eastham A R，Dawson G E.Detection of broken bars in the cage rotor on an induction machine［J］.IEEE Transactions on Industry Applications，1992，28（1）：165-171.

［11］谢颖，王零超，于涌源.笼型感应电动机转子非对称运行时磁场变化规律的研究 ［J］.中国电机工程学报，2011，31（30）：100-108.Xie Ying，Wang Lingchao，Yu Y Y.Magnetic field variation in squirrel-cage induction motor operating on asymmetric rotor［J］.Proceedings of the CSEE，2011，31（30）：100-108（in Chinese）.

［12］Gyftakis K N，Spyropoulos D V，Kappatou J C，et al.A novel approach for broken bar fault diagnosis in induction motors through torque monitoring［J］.IEEE Transactions on Energy Conversion，2013，28（2）：267-277.

［13］Hsu J S.Monitoring of defects in induction motors through air-gap torque observation［J］.IEEE Transactions on Industry Applications，1995，31（5）：1016-1021.

［14］Deleroi W.Broken bar in squirrel cage rotor of an induction motor，part1：description by superimposed fault currents［J］.Archiv für Elektrotechnik，1984（67）：91-99.

［15］Henao H，Razik H，Capolino G A.Analytical approach of the stator current frequency harmonics computation for detection of induction machine rotor faults［J］.IEEE Transactions on Industry Applications，2005，41（3）：801-807.

［16］侯新国，吴正国，夏立.基于 Park矢量模平方函数的异步电动机转子故障检测方法研究［J］.中国电机工程学报，2003，23（9）：137-140.Hou X G，Wu Z G，Xia L.A method for detecting rotor faults in asynchronous motors based on the square of the park’s vector Modulus［J］.Proceedings of the CSEE，2003，23（9）：137-140（in Chinese）.

Characteristic Performance Analysis of Traction Motor on EMU with Broken Bars Using FEM

LI Yongxin，GE Xinglai
（College of Electrical Engineering，Southwest Jiaotong University，Chengdu 610031，China）

The calculation model of motor operating on asymmetric rotor was defined taking a traction squirrel-cage induction motor in CRH2 as sample.Based on the basic principle of numerical analysis，magnetic field in the motor and currents in the bar were calculated for both normal motor and broken-bar motor using the Jmag software and the impact of broken-bar fault on them were summed up.According to the special control methods of electrical multiply unit（EMU），the motor with two broken bars was simulated at different work points，and the variation of characteristic component was summed up.The work in the paper laid the foundation of diagnosis method for broken rotor bar fault，especially for traction motor in EMU.

EMU traction motor；broken-bar fault；magnet field in motor；characteristic components；finite element method（FEM）

李永新

李永新（1990-）通信作者，男，硕士研究生，研究方向：电机故障诊断，E-mail：mingfengzhige@163.com；

葛兴来（1979-），男，工学博士，副教授，研究方向：电力牵引交流传动及其控制，变流器控制稳定性分析，E-mail：xlgee@163.com。

10.13234/j.issn.2095-2805.2015.1.41

：TM 3

：A

2014-07-28

国家自然科学基金项目（51277153）；中央高校基本科研基金项目（2682013ZT19，2682013CX017）

Project Supported by National Natural Science Foundation of China（51277153）；Fundamental Research Funds for the CentralUniversities（2682013ZT19，2682013CX017）