基于Salamon模型的采空区冒落矸石加载机理分析∗
王 猛 李文峰
(中国矿业大学矿业工程学院,江苏省徐州市,221116)
★煤炭科技·开拓与开采★
基于Salamon模型的采空区冒落矸石加载机理分析∗
王 猛 李文峰
(中国矿业大学矿业工程学院,江苏省徐州市,221116)
采用数值计算方法分析井工开采煤矿矿山压力与岩层控制问题时,采空区冒落矸石的加载机理、合理本构模型及输入参数困扰着很多学者,直接影响着数值模型的输出结果。为了解决上述问题,首先研究了工作面回采后直接顶岩块垮落、堆积、密实的过程,提出了冒落矸石在压缩前期应变迅速增加、后期杨氏模量和应力迅速增加的加载机理;同时基于Salamon和Terzaghi采空区理论模型优缺点的分析,指出Salamon模型应用范围更广,并采用有限差分软件FLAC3D里的双屈服本构模型模拟了采空区冒落矸石的特殊加载机理,工程实例分析揭示了所建立的数值计算采空区模型围岩应力分布规律与理论研究结果基本一致,模型合理可靠。
采空区 加载机理 Salamon模型 采空区模型 双屈服本构模型
长壁工作面开采后,采空区上方逐渐形成垮落带、裂隙带、弯曲下沉带,垮落带冒落矸石将首先自由堆积在采空区,并随上覆岩层的下沉而逐渐压缩密实,直至达到新的应力平衡。显然,冒落矸石的加载机理及密实状态将显著影响采空区围岩的应力场。当采用数值计算软件分析矿山压力问题时,必须考虑采空区冒落矸石的压实过程,才能得到合理的采空区围岩应力分布规律。
目前,许多学者对于采空区冒落矸石加载特性展开了相关的研究,如Pappas基于理论模型推测了冒落矸石的力学参数,认为其杨氏模量介于6.89 MPa与2.069 GPa之间;Terzaghi和Salamon基于岩石力学基本理论,得到了采空区冒落矸石加载过程的应力应变曲线,为数值计算采空区模型的建立提供了依据;Wilson研究认为采空区边缘应力为0,然后向采空区中央逐渐增大,当距离采空区边缘达到0.2~0.3倍的煤层埋深时,采空区应力基本恢复到原岩应力水平。
由于缺乏准确的现场实测结果,校验基于理论模型建立的采空区数值计算模型的合理性,仍然是一个研究难点。本文基于采空区冒落矸石的加载机理的研究,讨论了现存采空区理论模型的优缺点,进一步通过实例分析指出采空区模型在数值计算中的应用。
1 采空区冒落矸石的加载机理
由于采空区应力环境及块体接触围压间的不同,冒落矸石的加载机理差异性较为明显。以利民煤矿09113工作面为例,工作面回采后,在裂隙带及弯曲下沉带岩层下沉、压缩作用下,冒落带矸石经历密实块体裂隙和冒落矸石应力恢复2个阶段,其中,矸石冒落初期,由于块体间的自由堆积导致初始裂隙过大,随着上覆岩层的持续下沉块体间的裂隙将被密闭压实,之后,将有效承载上覆岩层的重力,并最终达到新的应力平衡状态(通常略小于原岩应力)。

图1 采空区块体与典型煤岩块加载对比曲线
事实上,实际中是不可能准确区分上述2个阶段,图1给出了典型的煤岩加载(曲线1)和与采空区冒落矸石加载(曲线2)的对比曲线,由图可知,采空区冒落矸石的压缩曲线明显与典型的煤岩加载曲线不同,若将采空区冒落带内的所有矸石看作一个统一的受力体,其具有以下加载规律:第一阶段内受力体的杨氏模量及应力缓慢增加,而应变则迅速增大;第二阶段杨氏模量及应力迅速增大,而应变则缓慢增大。
Pappas采用数字成像技术将冒落矸石等比例缩小,按照现场冒落矸石表面光滑度和形状进行样品的实验室加工,考虑现场实测孔隙率的情况下,将仿真样品置于容器中进行压缩试验,得到了采空区不同岩性块体的应力应变曲线,见图2,并回归得到了切线模量、割线模量与应力的关系式:

式中:Es——割线模量;
Et——切线模量;
σ——压缩应力。
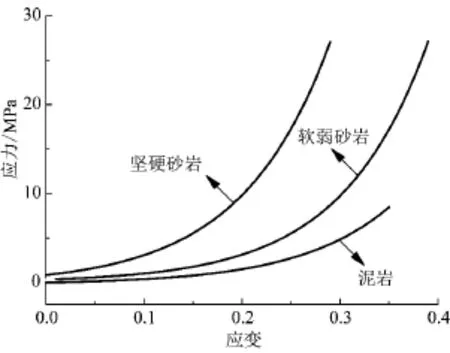
图2 不同岩性采空区矸石加载曲线
由图2分析得知,采空区冒落矸石无论何种岩性,其室内试验获得的应力应变曲线均表现出前期应变急剧增加,后期应力、杨氏模量急剧增加的总体规律,与此前关于冒落带块体经历的两个阶段的描述基本一致,差别在于各岩性的冒落矸石承载起始点(曲线拐点)不同,冒落矸石强度越小,其开始承载时对应的应变就越大。
2 采空区理论模型
为了量化采空块体的应力应变关系,Salamon和Terzaghi开发了不同的采空区理论模型。其中, Salamon采用岩土力学基本理论将冒落块体视为颗粒物质,在分析岩块孔隙率、碎胀系数、压缩应力的基础上,推导了采空区冒落岩块的应力应变计算式:

式中:σ——采空区应力,MPa;
ε——采空区应变;
εm——采空区最大应变;
E0——初始模量,MPa;
σc——岩石抗压强度,MPa;
b——碎胀系数;
hm——采高,m;
hn——垮落带高度,m。
Terzaghi将采空区材料应力应变曲线的正切模量视为加载应力的线性函数,推导了应力应变微分方程,借助于边界条件(初始情况下应力应变均为0)进行求解,得到如下计算式:
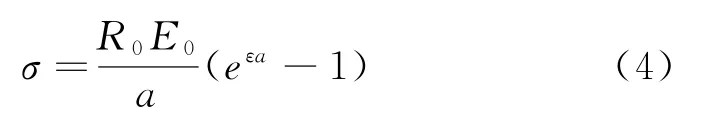
式中:R0、ɑ——计算常数。
为评估上述2种采空区理论模型的可靠性, Pappas将实验室力学测试结果分别与Salamon和Terzaghi的理论模型进行了比对,如图3所示,对于坚硬砂岩,Salamon和Terzaghi理论模型与平均实验结果均较为一致;而采空区冒落矸石岩性从坚硬砂岩向软弱砂岩和泥岩过渡时,Salamon理论模型则接近平均实验结果,由此可知,Terzaghi和Salamon理论模型虽然均可良好地反映采空区冒落岩块的加载机理,显然Salamon理论模型更具有普遍意义。

图3 Salamon和Terzaghi理论模型的比较
3 实例应用
由于采空区冒落矸石与完整煤块体的加载机理具有本质上的区别,当采用数值计算方法研究采空区冒落矸石加载特性时,必须首先研究采空区冒落块体合理的本构模型和输入参数,使其具有前文所述的加载特征,因而,建立数值计算模型时,主要确定以下内容:数值计算软件选择;采空区理论模型选择;采空区冒落矸石的本构模型和参数选择;采空区材料和理论模型加载特征曲线的匹配;校验计算输出结果中采空区围岩应力分布与理论研究或现场实测结果是否一致。
3.1 生产地质条件
乌海能源利民煤矿09113工作面位于091采区,开采的9#-1煤层以及9#-2煤层为近水平煤层,煤层平均埋深300 m,中间夹矸约0.3 m,平均采高3.6 m,煤层顶底板岩性如表1所示,采掘工程平面图如图4所示。09113工作面长200 m,推进长度为930 m,相邻两工作面间的区段煤柱宽5 m,取图中R-R′断面建立平面应变数值计算模型,模型包括09113工作面采空区、区段煤柱、09114工作面运输巷和09114工作面。

表1 9#煤层顶底板柱状
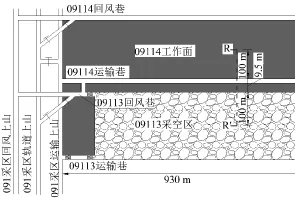
图4 采掘工程平面图
3.2 数值计算工具的选择
目前,采矿学者常使用的软件主要包括:有限元ABAQUS、有限差分FLAC3D(FLAC)、离散元UDEC(3DEC)等,而相对于有限元软件,有限差分和离散元软件的应用范围更广。由于采空区模型中包括采空区材料,因此需要分析FLAC和UDEC的适用性问题。理论上讲,工作面回采后,采空区上覆岩层将破裂为不均匀尺寸的块体,显然,块体的尺寸和堆积方式将显著影响最终的采空区应力分布规律,UDEC需要用户提前对块体尺寸进行划分,违背了采空区冒落块体尺寸的不可预知性,同时当离散元模型较大并需要在同一岩层中划分多种尺寸的块体时,建模工作量将非常庞大,因此UDEC具有应用方面的局限性;而有限差分方法并不需要用户提前划分冒落带块体尺寸,同时,已有学者验证了其适用性,基于此,本文将建立FLAC3D的数值计算模型分析采空区冒落矸石的加载特性。
3.3 采空区理论模型的选择
基于前面室内试验结果和Terzaghi、Salamon理论模型的比较,证明Salamon理论模型更具普遍意义,且由于试验工作面垮落带岩层多为泥岩、砂质泥岩等软弱/中硬岩层,因此,本文选用Salamon理论模型作为数值计算采空区模型的校验标准。
3.4 数值计算模型建立
根据表1所示9#煤层顶底板条件,建立如图5所示的平面应变数值计算模型,对应图4中R-R′剖面。模型尺寸209.5 m×149.22 m×1 m,在模型上下部分别建立了50 m、60 m厚的岩层,以避开边界影响。各煤岩层均采用摩尔库伦本构模型,材料输入参数如图5左侧表格所示。模型上边界施加5.65 MPa垂直方向的载荷,侧压系数取1.2。此外,09113工作面回采后上覆岩层垮落带范围及冒落岩块的本构模型和输入参数将在后面展开分析。建立图5所示模型并给原岩赋值。

图5 数值计算模型(R-R′剖面)
3.5 数值计算采空区模型
采用Salamon理论模型,需要首先确定式(3)中的各项参数,根据钱鸣高院士关于“竖三带”的划分依据,确定煤层上方5.31 m炭质泥岩、3.60 m砂质泥岩、1.69 m细粒砂岩组成煤层直接顶,即冒落带岩层厚10.6 m,工作面采高3.6 m,则碎胀系数b为1.34,最大应变εm为0.25,采空区材料初始模量E0取15.91 MPa,岩石抗压强度σc取30 MPa,将各参数代入式(3)可得Salamon理论模型下采空区材料应力应变关系,如表2所示。
FLAC3D中有多个本构模型均可模拟采空区冒落矸石加载机理,但研究表明双屈服本构模型效果最佳,双屈服材料的输入参数可分为材料应力应变关系和材料参数两组,前者已由表2给出,确定材料参数时,需要不断调整材料参数赋值,使数值计算模型输出的块体应力应变曲线与理论模型的应力应变曲线精确吻合,匹配曲线如图6所示,最终确定采空区材料参数为体积模量16.39 GPa、剪切模量7.45 GPa、摩擦角22°、膨胀角10°、杨氏模量19.41 GPa、泊松比0.3。
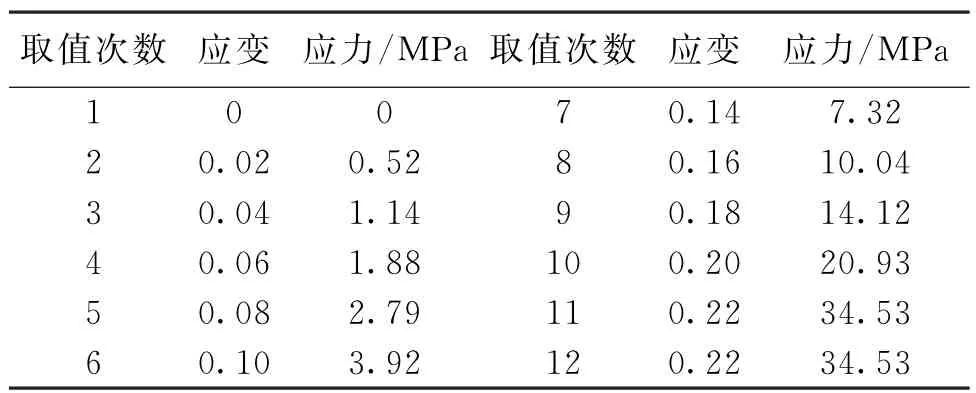
表2 FLAC3D采空区模型材料应力应变关系表
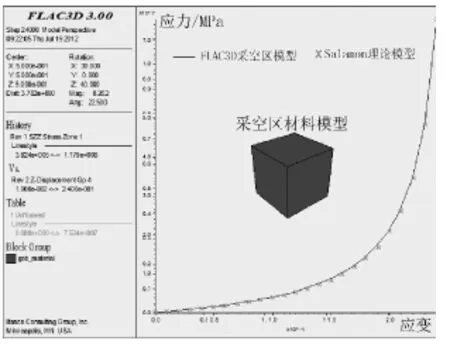
图6 FLAC3D采空区模型和Salamon理论模型的应力应变曲线对比
3.6 采空区模型合理性论证
将确定的采空区材料参数输入图5所示的数值计算模型中,运算平衡后,取出采空区底板垂直应力,并将采空区底板垂直应力与原岩应力的比值绘制如图7左侧所示的曲线图,由图7可知,采空区0点(图7中P点,对应现场区段煤柱边缘位置)的垂直应力为0.4 MPa,约为原岩应力的5%,采空区内最大应力位于距区段煤柱100 m位置P′处,量值约为6.73 MPa,恢复至原岩应力的90%,当距离区段煤柱60 m时(约为煤层埋深的20%),采空区应力恢复到6.2 MPa,约为原岩应力的83%,与以往研究结论基本一致,表明建立的采空区数值计算模型合理可靠。

图7 采空区围岩应力分布规律
4 结论
(1)分析了工作面回采后直接顶岩块垮落、堆积、密实的过程,提出了冒落矸石与完整煤岩试块加载机理的显著区别在于冒落矸石在压缩前期应变迅速增加,而后期杨氏模量和应力则迅速增加。
(2)研究了Salamon和Terzaghi采空区理论模型的优缺点,指出了Salamon理论模型普遍适用于软弱、中硬和坚硬垮落带岩层,而Terzaghi理论模型仅可应用于坚硬垮落带岩层。
(3)提出了建立数值计算采空区模型的5个步骤:数值计算软件选择;采空区理论模型选择;采空区冒落矸石的本构模型和参数选择;采空区材料和理论模型加载特征曲线的匹配;校验计算输出结果中采空区围岩应力分布与理论研究或现场实测结果是否一致。
(4)提出了有限差分FLAC3D里的双屈服本构模型可模拟采空区冒落矸石的特殊加载机理,同时,实例分析进一步揭示本文建立的数值计算采空区模型周围的应力分布与理论研究结果基本一致,模型合理可靠。
[1] 钱鸣高,石平五,许家林.矿山压力与岩层控制[M].徐州:中国矿业大学出版社,2010
[2] Peng S S.Longwall Mining[M].West Virginia University Press,2006
[3] Pappas D,Mark D.Behavior of simulated longwall gob material[M].Pittsburgh:Bureau of Mines, 1993
[4] Salamon M D G.Mechanism of caving in longwall coal mining[A].Proc.of the 31st U.S.Symposium of Rock Mechanics[C],Golden,West Virginia University Press,1990
[5] 何富连,吴焕凯,李通达等.深井沿空掘巷围岩主应力差规律与支护技术[J].中国煤炭,2014(3)
[6] 孟超,李学华.沿空掘巷锚杆支护参数敏感性分析与应用[J].中国煤炭,2013(3)
[7] 柏建彪,侯朝炯,黄汉富沿空掘巷窄煤柱稳定性数值模拟研究[J].岩石力学与工程学报,2004(20)
Analysis on the loading mechanism of caving gangues in goaf based on Salamon model
Wang Meng,Li Wenfeng
(School of Mines,China University of Mining and Technology,Xuzhou,Jiangsu 221116,China)
When the numerical modeling method was applied to analyze the mining pressure and surrounding rock control in underground coal mines,lots of scholars were puzzled by some problems such as the loading mechanism of caving gangues,reasonable constitutive model and input parameters,so the output results of the numerical model were directly influenced.In order to solve these questions,the caving,stacking and compacting processes of immediate roof rock after working face mining were researched firstly,then the loading mechanism was put forward which including that the strain in earlier stage of compression,the Young modulus and stress in later stage of compression increased rapidly.According to the merit and demerit analysis of Salamon and Terzaghi models,applied range of Salamon model was more extensive,and the double-yield constitutive model of Fl AC 3D was adopted to simulate the special loading mechanism of caving gangue in the goaf.Engineering projects showed that the stress distribution law of surrounding rock calculated by the established numerical model was almost same with the theoretical research result,so the model was reasonable and reliable.
goaf,loading mechanism,Salamon model,goaf model,double-yield constitutive model
TD823.83
A
王猛(1986-),男,江苏徐州人,博士研究生,从事巷道围岩控制理论与支护技术方面的研究。
(责任编辑 张毅玲)
江苏省2013年度普通高校研究生科研创新计划项目(CXLX13_952)

