不对称船体结构总纵强度计算方法及影响分析

崔海鑫 李 聪

（中国船舶及海洋工程设计研究院 上海200011）

引 言

在传统的船体结构设计中，其横剖面左右舷一般呈对称或近似对称布置。但有时由于总体布局的特殊需要，往往会引起结构设计的不对称性，如舱室布置、水线以上总体线型及结构大开口的不对称布置等，而水线以上总体线型及结构大开口的不对称布置影响尤为明显。结构的不对称设计将会直接影响到船体梁剖面特性，导致总纵弯曲正应力重新分布，左右舷应力分布不对称，从而影响船体总纵强度。而在设计初期通常采用船体梁理论计算总纵强度，对于不对称结构的船体梁总纵弯曲正应力计算方法目前尚没有过多研究，也没有指出明确的计算方法，因此本文拟结合有限元计算方法提出船体梁的总纵弯曲正应力简化计算方法，并分析不对称结构对船体总纵强度产生的影响。

1 不对称船体梁剖面弯曲正应力计算方法

船体横剖面由多种构件组成，如甲板板、船底外板、内底板、舷侧外板、纵舱壁、纵桁以及纵骨等。为计算中横剖面要素应建立全局坐标系，取纵向为X轴，甲板中心向左舷方向为Y轴，垂直于甲板向上方向为Z轴，坐标原点为基线与中纵剖面交点。

剖面要素计算公式为：

式中：dF为剖面各微截面面积。

1.1 剖面形心位置

由式（1）、式（2）求出：

相对于oy轴形心坐标zC：

相对于oz轴形心坐标yC：

1.2 剖面形心惯性矩和剖面模数

假定：y0为水平弯曲中和轴；z0为垂向弯曲中和轴。

相对y0轴的弯曲惯性矩为：

相对z0轴的弯曲惯性矩为：

相对于形心位置（yC，zC）的惯性积为：

在外底处的垂向弯曲剖面模数（相对于y0轴）：

在型深处的垂向弯曲剖面模数（相对于y0轴）：

在左舷舷侧边线的水平弯曲剖面模数（相对于z0轴）：

在右舷舷侧边线的水平弯曲剖面模数（相对于z0轴）：

式中：D为型深，m；B为型宽，m。

1.3 主惯性轴坐标系下的惯性矩

中和轴的转角由下式求出：

按 角旋转至主惯性轴方向，在主惯性轴坐标系下的惯性矩为：

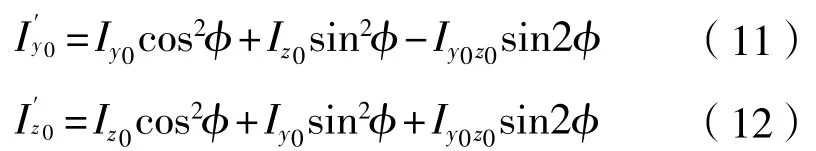
1.4 模型结构的纵向弯曲正应力

模型结构的弯曲正应力用简单梁理论公式计算。对称剖面：

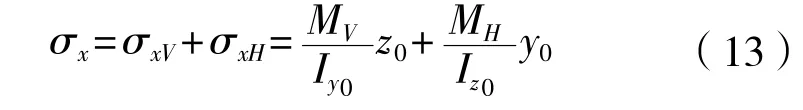
不对称剖面：将船体垂向弯矩MV和水平弯矩MH沿剖面主惯性轴矢量分解，形成针对主惯性轴的垂向弯矩 和水平弯矩 ，运用简单梁理论公式分别计算垂向和水平弯曲正应力，进而矢量相加即得到计算位置的纵向弯曲正应力，计算公式为：

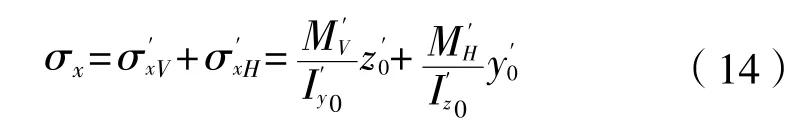
式中：MV为对称剖面船体梁垂向弯矩；MH为对称剖面船体梁水平弯矩；为不对称剖面船体梁垂向弯矩；为不对称剖面船体梁水平弯矩；为对称剖面垂直惯性矩；为对称剖面水平惯性矩；为不对称剖面垂直惯性矩；为不对称剖面水平惯性矩。弯矩作用方向如图1和图2所示。

图1 对称剖面弯矩方向示意图

图2 不对称剖面弯矩方向示意图

本文只考虑在垂向弯矩和水平弯矩作用下船体梁的纵向弯曲正应力，不考虑由于扭转而引起的翘曲应力（对于常规船舶，由于船体梁具有充分大的扭转刚性和扭转强度，扭转引起的翘曲应力一般较小，不占主导地位）。

2 船体梁理论计算剖面纵向弯曲正应力

以某船型为例，典型的船体梁横剖面不对称特点包括以下几方面：

（1）左右舷线型不对称，左舷线型在1甲板与3甲板之间部分向外有较大延伸；

（2）左右舷结构的总体布局存在一定差异，1甲板至4甲板之间纵舱壁位置左右舷不一致。

图3 典型的船体梁不对称横剖面

参照第1节中的计算公式来计算横剖面的剖面特性，横剖面要素参见表1。

表1 横剖面要素表

本文以顶浪工况为例，施加垂向弯矩MV（包括静水弯矩MS和垂向波浪弯矩MWV），弯矩方向指向y0轴。将该弯矩值沿轴轴方向进行矢量分解：

在模型中分别选取四个节点A、B、C、D进行校核，节点位置分布对于横剖面左上角点、右上角点、左下角底板与纵舱壁交点、右下角底板与纵舱壁交点。分别计算出各弯矩分量所引起的相应弯曲正应力分量，进而求得合成弯曲正应力，计算结果分别见表2、表3。

表2 弯矩：

表2 弯矩：

计算点距轴弯矩的垂直距离Z /m 计算点处的弯曲正应力σ /MPa A B C D A B C D 2.726×109 392.87 10.73 13.14 12.39 11.1 74.45 91.17-85.97-77.02/相对于轴 的惯性矩/m4

表3 弯矩：

表3 弯矩：

弯矩 / 相对于轴 的惯性矩 /m4计算点距轴 的垂直距离Y /m 计算点处的弯曲正应力σ /MPa A B C D A B C D 0.197×109 559.50 17.87 15.45 7.78 10.18 6.29-5.44 2.74-3.58

同时计算假定中和轴不偏转时剖面A、B、C、D四节点的纵向弯曲正应力，计算结果见表4。

表4 弯矩：

表4 弯矩：

弯矩MV / 相对于轴 y0的惯性矩 /m4计算点距轴 y0 的垂直距离Z /m 计算点处的弯曲正应力σ /MPa A B C D A B C D 2.733×109 392.00 11.993 11.993 11.807 11.807 83.61 83.61-82.32-82.32

不对称剖面的纵向合成弯曲正应力见表5，中和轴偏转与不偏转的弯曲正应力对比结果见表5。

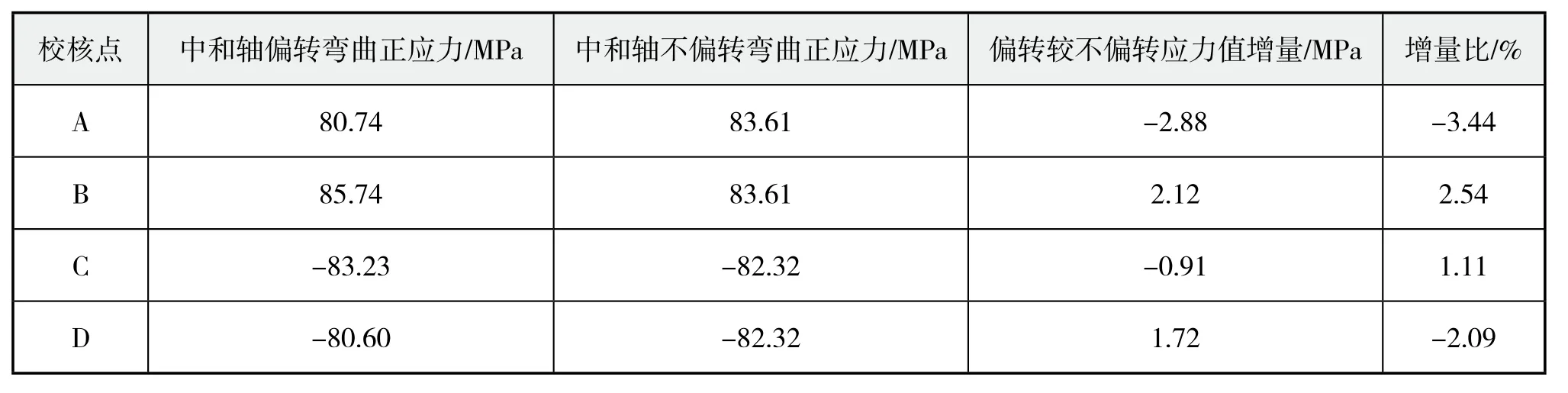
表5 中和轴偏转与不偏转应力对比

从应力对比结果来看，应力最大位置出现在右舷甲板端部。相对于中和轴不发生偏转的情况来说，不对称结构中和轴发生偏转后的总纵弯曲正应力的峰值较中和轴不发生偏转的理想对称结构有一定的增量，可以看出不对称结构对船体梁的总纵弯曲正应力分布产生一定的影响，其影响与中和轴的偏转角度有关，角度越大，增量比越大。因此，设计时需根据剖面的不对称程度来考虑总纵强度的计算方法。

3 有限元方法计算船体纵向弯曲正应力

3.1 有限元模型

针对船体中横剖面设计方案，建立有限元模型。沿船长方向拉长，拉长的长度是最大甲板高的6倍以上，以减小边界条件对所关心剖面应力分布的影响。在模型中每隔四档肋位设置一强框架，不对称结构有限元模型如图4所示。有限元模型中所有板构件用壳单元模拟，纵桁、纵骨、强框架和扶强材用梁单元模拟。

图4 不对称结构有限元模型

3.2 计算载荷及边界条件

计算工况采用与梁理论计算相同的顶浪工况，垂直于底部方向施加均布载荷，模拟实船船中弯矩大两端弯矩小的受力状态，使船中剖面弯矩与梁理论计算所用弯矩值相同（即2.733×109N·m），船体梁为中拱状态。

在模型两端建立MPC单元，施加端点约束条件，参照《CCS结构强度直接计算指南》：

（1）中纵剖面内节点的纵向、横向位移为0，绕中纵剖面内两个坐标轴的角位移为0，即：δx、δy、θx、θz皆为 0 ；

（2）船体梁可发生绕Y轴和Z轴的转动，故端面约束取为 ：两端独立点δx、δy、δz、θx皆为 0。示意图见图5。

图5 计算载荷及边界条件

3.3 有限元计算结果

利用有限元计算分析，选取模型弯矩最大的中间剖面，应力云图见图6。

图6 横剖面纵向弯曲正应力云图

在有限元模型中选取与梁理论计算相同位置的四个节点A、B、C、D，读取其纵向弯曲正应力，列于表6中。

表6 有限元计算总纵弯曲正应力

梁理论计算结果与有限元计算结果对比见下页表7。

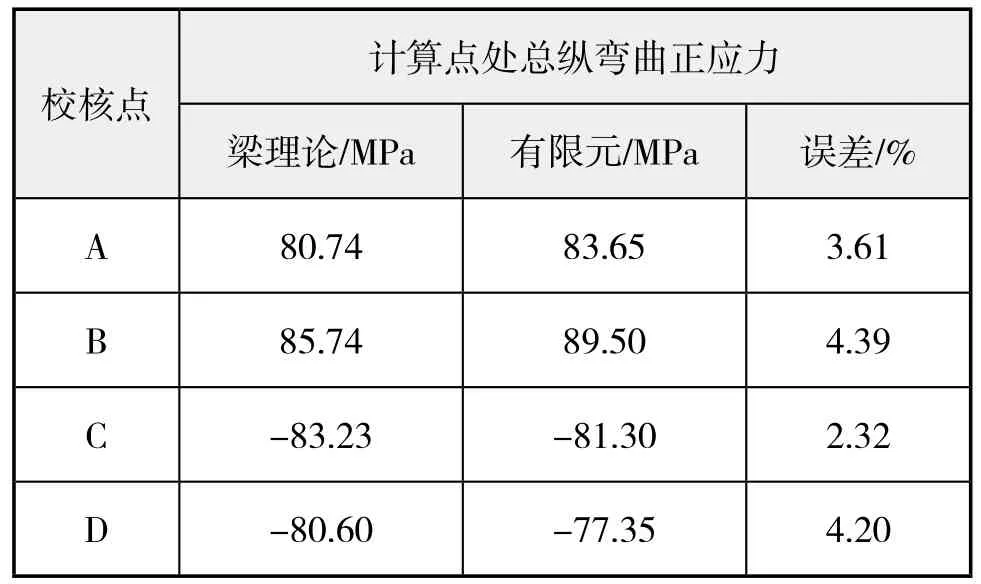
表7 梁理论与有限元计算弯曲正应力对比

从上面计算结果对比可见：两种方法计算结果相差很小，也验证了针对目标船型，应用梁理论计算不对称结构总纵弯曲正应力的计算方法的准确性。但是，由于有限元计算方法求得的总纵弯曲应力幅值相对梁理论计算方法略大3%～5%，所以，在应用不对称结构梁理论方法求解总纵弯曲应力时应至少保留5%的剖面模数余量，船体梁结构的不对称性越大，为剖面模数所留余量应更多。

由于目标船型船体结构的不对称性相对较小，为验证梁理论计算方法是否适用于结构不对称性较大的船型特殊状态（例如遭到武器攻击、碰撞、火灾等意外事件后导致局部损伤），笔者还尝试将目标船型的右舷5甲板以上结构全部删除后的极端状态分别采用梁理论法和有限元法进行比较分析。有限元法的计算结果表明：当船体结构的典型剖面表现出强不对称性时，偏转的中和轴不再是一条直线，梁理论计算方法的计算误差随着结构不对称性的增加而急剧增加，此时应用梁理论偏转中和轴的计算方法来计算船体梁总纵弯曲正应力将不再适用。

4 结 论

本文通过对不对称船体结构梁理论弯曲正应力计算方法的研究，得出以下结论：

（1）针对不对称性程度较小的船体横剖面，运用梁理论计算总纵强度时，应考虑横剖面中和轴的偏转效应，可以采用将弯矩沿剖面主惯性轴方向矢量分解求取应力分量，进而合成总纵弯曲正应力的方法进行计算。

（2）针对船体结构损伤后不对称性程度较大的船体横剖面，船体梁法计算总纵强度计算方法不完全适用，偏转后的中和轴不再是一条直线，其理论计算方法有待进一步研究，建议采用有限元方法进行精确计算。

（3）不对称结构的总纵弯曲正应力左右舷分布不对称，其峰值相较于理想对称结构有一定增量。在设计初期对于总强度余量不大的船来说，如果忽略不对称因素，容易造成实际总强度不满足要求的情况；以致在设计后期产生很大工作量，因此在设计初期需根据船体的不对称程度来考虑总纵强度的计算方法。若船体明显不对称，偏转角度较大，需要运用不对称剖面的总纵强度简化计算方法进行总强度的计算与校核。

（4）船型总设计师在进行总布置规划时，需考虑船体结构的不对称性越大，引起船体结构基于总纵强度的特殊加强将越多。在设计条件允许的情况下，应尽量将船体结构关于中心线对称布置。

［1］ 金忠谋.材料力学［M］.北京：机械工业出版社，2003.

［2］ 郑学祥、杨代盛、桑国光.船体强度与结构设计［M］.上海：上海交通大学出版社，1962.

［3］ 中国船级社.散货船结构强度直接计算分析指南［M］.北京：人民交通出版社，2003.

［4］ MSC.Nastran有限元分析理论基础与应用［M］.北京：科学出版社，2004.

［5］ 温保华.不对称船体结构的非线性响应研究［D］.哈尔滨：哈尔滨工程大学，2003.