基于CCS软件的数字滤波器实验设计
姜恩华,袁广宇,陈得宝,杨一军
(淮北师范大学物理与电子信息学院,安徽淮北235000)
数字信号处理课程主要讲述的经典数字滤波器,分为无限长脉冲响应IIR滤波器和有限长脉冲响应FIR滤波器两种类型,如何开展数字滤波器实验教学一直是数字信号处理课程教学的难点。本文采用双线性变换法实现IIR滤波器的实验设计,采用窗函数法实现FIR滤波器的实验设计。在CCS集成开发环境下[1],采用C语言编写程序,以IIR带通滤波器实验设计为例,讨论IIR滤波器的实验设计过程和程序实现。以FIR高通滤波器实验设计为例,讨论FIR滤波器的实验设计过程和程序实现。并通过比较滤波器输入序列x(n)和输出序列y(n)的频谱,验证实验结果的正确性。
1 CCS软件环境
文献[2-3]探索了CCS用于“信号处理”课程的实验教学,该方法需要DSP硬件设备的支持;文献[4-5]探索了采用CCS和MATLAB相结合的方法,该方法需要MATLAB软件的支持。本文研究通过CCS3.3软件搭建完成数字滤波器实验设计的软件实验环境,选择C5402 Device Simulator作为软件模拟器,根据数字滤波器实验设计的数据和程序要求编写CMD存储器配置文件;通过CCS软件菜单栏中的View菜单中的Graph子菜单中的time/frequency[6],并借助time/frequency菜单,观察数字滤波器输出序列y(n)的波形和频谱。在CCS集成开发环境下,通过C语言编写程序实现数字滤波器实验设计,熟练掌握CCS软件以工程文件组织程序文件的方法,首先建立一个工程文件[6],然后把程序文件添加到工程文件中,对工程文件进行编译并加载到软件仿真器中,然后运行程序,观察数字滤波器设计的实验结果。
2 IIR滤波器实验设计
IIR滤波器实验设计主要分为三个步骤。首先,输入序列x(n)设计;其次,根据IIR滤波器设计的技术指标,通过双线性变换法,得到模拟滤波器的技术指标,通过模拟滤波器设计(例如:巴特沃斯滤波器设计),求得模拟滤波器的系统函数Ha(s),根据Ha(s)和H(z)的分子分母多项式系数关系表[7],求得系统函数H(z)的分子分母多项式的系数,从而得到IIR滤波器的常系数差分方程;再次,把x(n)和初始条件代入常系数差分方程,通过递推方法求解常系数差分方程,由此求得IIR滤波器的输出序列y(n)。本文以IIR带通滤波器实验设计为例,在CCS集成开发环境下,通过C语言编写程序,讨论IIR带通滤波器实验设计的过程。IIR低通、高通和带阻滤波器也可以按照此方法进行设计。
2.1 输入序列x(n)设计
假设IIR带通滤波器的通带下限截止频率为ωp1,通带上限截止频率为ωp2,ω∈[-π,π]时,通带范围为ωp1≤|ω|≤ωp2,阻带范围为ωp2< |ω|≤π,0≤|ω|≤ωp1[8]。
假设IIR带通滤波器的通带归一化截止频率为:bandpass1=0.24;bandpass2=0.26,则IIR带通滤波器的通带截止频率为:ωp1=bandpass1*2*pi=0.48π;ωp2=bandpass2*2*pi=0.52π。
根据通带截止频率ωp1和ωp2,设计的输入序列x(n)如(1)式所示。
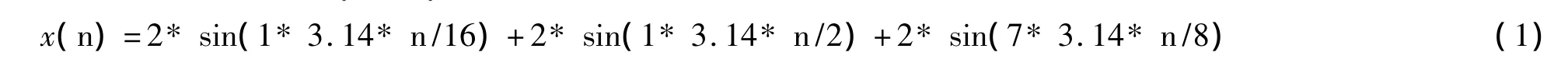
在C语言的main主函数中,把(1)转换为C语言语句,假设输入序列的长度为N=256,求出输入序列x(n),借助time/frequency菜单观察x(n)的时域波形如图1所示,频谱如图2所示。

图1 输入序列x(n)的时域波形
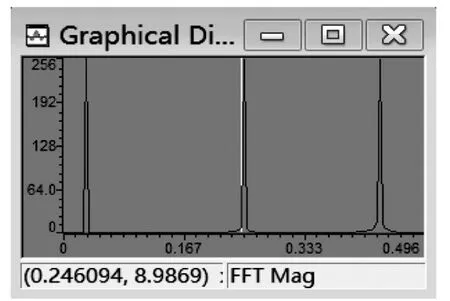
图2 输入序列x(n)的频谱
2.2 求解IIR带通滤波器的系统函数H(z)程序设计
假设模拟低通滤波器的归一化的系统函数如(2)所示。

通过对(2)去归一化,把(2)转换为IIR带通滤波器的系统函数Ha(s),如(3)所示[7]。

根据通带截止频率ωp1和ωp2,通过双线性变换法频率变换公式,假设 T=2秒,把 ωp1和ωp2转换为模拟域频率Ωp1和Ωp2,如(4)所示。

根据IIR带通滤波器的通带宽度B=Ωp2-Ωp1和中心频率=Ωp1*Ωp2计算公式,计算出通带宽度B和通带中心频率Ω0,代入(3),求出模拟带通滤波器的系统函数Ha(s)。
根据Ha(s)分子分母多项式系数,查找系数关系表[7],由于Ha(s)的阶数为2,所以把系数关系表中k=2的公式转换为C语言的语句,编写求解H(z)的分子分母多项式系数的子程序,在C语言的main主函数中,调用此子程序,求得H(z)的分子分母多项式的系数,从而得到IIR带通滤波器的常系数差分方程。
2.3 递推方法求解常系数差分方程程序设计
采用递推方法求解IIR滤波器的常系数差分方程的步骤如下[7-9]:初始条件w2=w1=w0=0.
根据输入序列x(n)和初始条件,在C语言的main函数中,把递推方法求解差分方程的公式,转换为C语言的语句,计算出IIR带通滤波器的输出序列y(n),借助time/frequency菜单观察y(n)的时域波形如图3所示,频谱如图4所示。比较输入序列x(n)和输出序列y(n)的频谱,可以看出,输出序列y(n)就是输入序列x(n)的中频成分。
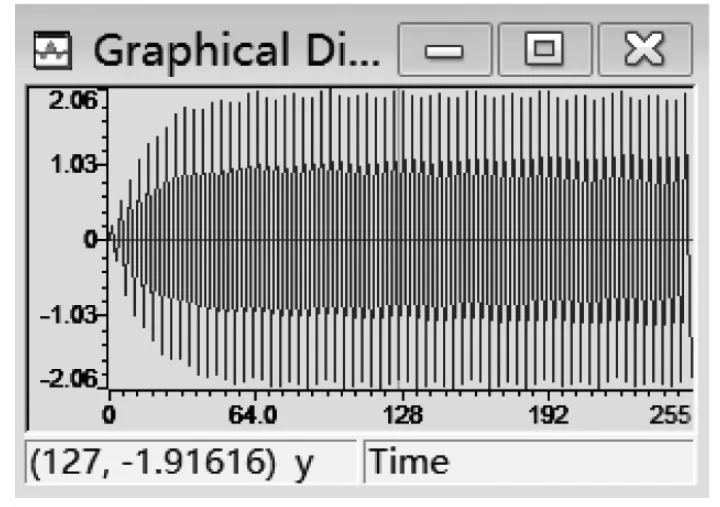
图3 输出序列y(n)的时域波形
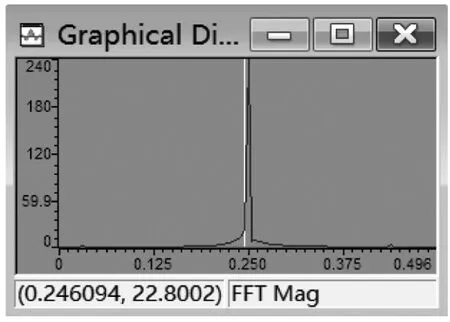
图4 输出序列y(n)的频谱
3 FIR滤波器实验设计
FIR滤波器实验设计主要分为三个步骤。首先,设计输入序列x(n);其次,根据FIR滤波器的类型,设计其单位脉冲响应h(n);再次,编写计算x(n)和h(n)的线性卷积子程序,计算FIR滤波器的输出序列y(n)。本文以FIR高通滤波器实验设计为例,在CCS集成开发环境下,通过C语言编写程序,讨论FIR高通滤波器的实验设计过程,FIR低通、带通和带阻滤波器也可以按照此方法进行设计。
3.1 FIR高通滤波器的单位脉冲响应h(n)设计
假设FIR数字高通滤波器的截止频率ωc=0.1π,则设计的FIR高通滤波器的单位脉冲响应h(n)如(5)所示[8]。
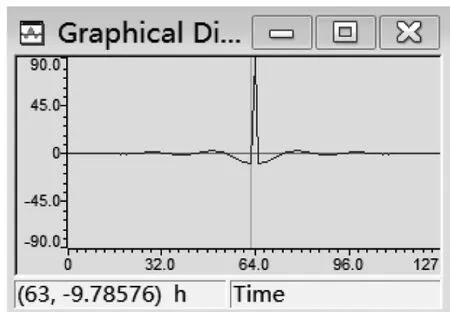
图5 单位脉冲响应h(n)的时域波形
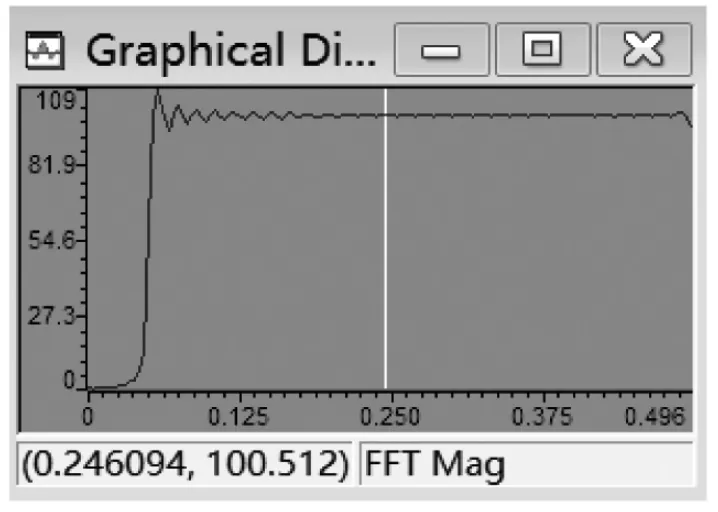
图6 单位脉冲响应h(n)的频谱
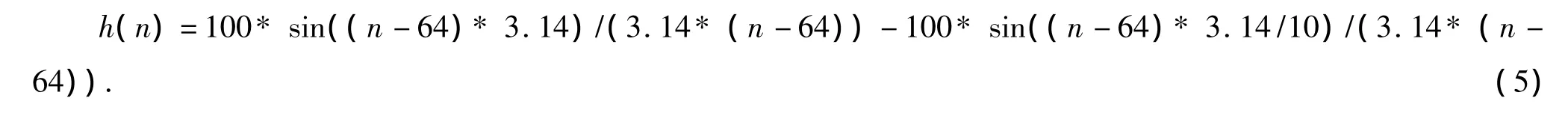
在C语言的main主函数中,把(5)转换为C语言语句,假设h(n)的长度N=128,计算单位脉冲响应h(n),借助time/frequency菜单观察h(n)的时域波形如图5所示,频谱如图6所示。
3.2 输入序列x(n)设计
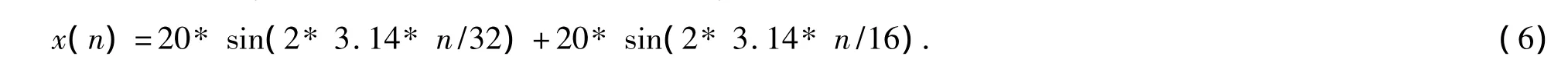
根据FIR高通滤波器的截止频率ωc=0.1π,输入序列x(n)设计为两个正弦序列的叠加,其中一个正弦序列的频率小于ωc,另一个正弦序列的频率大于ωc,如(6)所示。在C语言的main主函数中,把(6)转换为C语言语句,假设x(n)的长度N=128,计算出输入序列x(n),借助time/frequency菜单观察x(n)的时域波形如图7所示,频谱如图8所示。
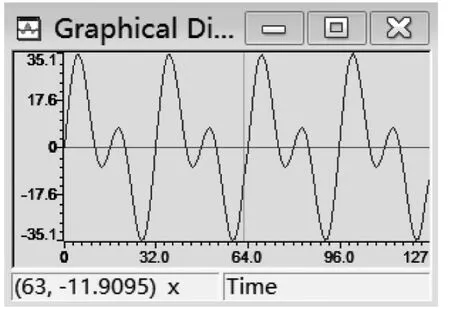
图7 输入序列x(n)的时域波形
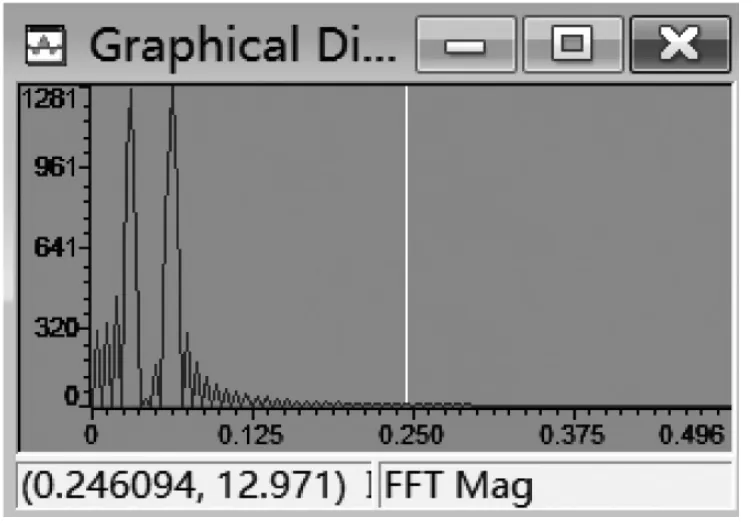
图8 输入序列x(n)的频谱
3.3 线性卷积子程序设计
FIR高通滤波器的常系数差分方程就是输入序列x(n)和单位脉冲响应h(n)的线性卷积计算公式,所以FIR高通滤波器的输出序列y(n)可以通过计算x(n)和h(n)的线性卷积求出。计算线性卷积的步骤分为:翻转、移位、相乘和求和[7-9],根据线性卷积的计算步骤编写计算线性卷积的子程序,此程序采用两重循环,外层循环为移位运算,循环变量为n,内层循环为相乘求和运算,循环变量为m,根据相乘求和的上下限确定内层循环的起始条件和终止条件,根据相乘求和时序列x(n)和h(n)的边界确定相乘求和时存放序列x(n)和h(n)的数组的下标,通过C语言编写线性卷积子程序。
在C语言的main主函数中,调用线性卷积子程序,计算输入序列x(n)和单位脉冲响应h(n)的线性卷积,求出输出序列y(n),借助time/frequency菜单观察y(n)的时域波形如图9所示,频谱如图10所示。比较输入序列x(n)和输出序列y(n)的频谱,可以看出,输出序列y(n)就是输入序列x(n)的高频成分,其周期N为16。
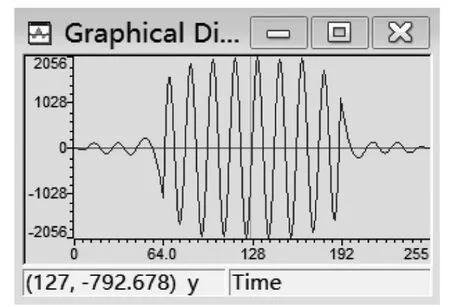
图9 输出序列y(n)的时域波形
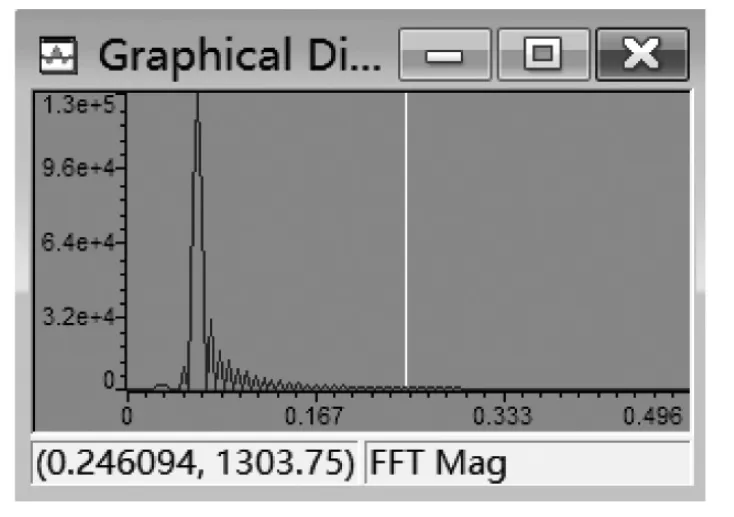
图10 输出序列y(n)的频谱
4 结语
综上所述,借助CCS3.3软件,选择C5402 Device Simulator作为软件模拟器,搭建了IIR和FIR滤波器实验设计的软件环境,采用C语言编写程序,采用双线性变换法实现IIR滤波器实验设计,采用窗函数法实现FIR滤波器实验设计,实验设计过程主要包括:首先,输入序列x(n)设计。其次,通过求解IIR滤波器的系统函数H(z),得到IIR滤波器的常系数差分方程;FIR滤波器的单位脉冲响应h(n)设计。再次,通过递推方法求解常系数差分方程,计算IIR滤波器的输出序列y(n);通过计算输入序列x(n)和单位脉冲响应h(n)的线性卷积,计算FIR滤波器的输出序列y(n)。以IIR带通滤波器和FIR高通滤波器实验设计为例,详细讨论了IIR和FIR滤波器实验设计过程。借助time/frequency菜单观察输入序列x(n)和输出序列y(n)的时域波形和频谱,比较x(n)和y(n)的频谱,并验证实验结果的正确性。
[1]Code Composer Studio(CCS)集成开发环境(IDE)[EB/OL].(2014-01-02)[2014-04-05].http://www.ti.com.cn/tool/cn/CCSTUDIO.
[2]刘成云,陈振学,孔慧.基于CCS的“信号分析与处理”实验教学[J].实验室研究与探索,2010,29(11):97-100.
[3]谢海霞,孙志雄.FIR 滤波器的 DSP 实现[J].电子器件,2012,35(5):554-557.
[4]李波,王冬霞.MATLAB在CCS集成编程环境中应用的研究[J].渤海大学学报:自然科学版,2010,31(1):84-88.
[5]梅志红,赵莉.基于CCS环境和MATLAB仿真的FIR数字滤波器实现[J].电气电子教学学报,2005,27(3):44-47.
[6]彭启琮.TI DSP集成化开发环境(CCS)使用手册[M].北京:清华大学出版社,2007.
[7]丁玉美,高西全.数字信号处理[M].2版.西安:西安电子科技大学出版社,2001.
[8]程佩青.数字信号处理教程[M].3版.北京:清华大学出版社,2007.
[9]A.V.奥本海姆,R.W.谢弗,J.R.巴克.刘树棠,黄建国,译.离散时间信号处理[M].2 版.陕西:西安交通大学出版社,2001.

