气候条件对光伏发电量影响浅析
北京科诺伟业科技股份有限公司 ■ 张玉娜 王伟 梁勃
0 引言
随着社会经济的飞速发展,各种所需能源与日俱增,传统燃料能源的全球储量正在逐步缩减,甚至面临枯竭。与此同时,环境需求也处于历史最为严峻的时刻,全球变暖、温室效应、雾霾弥漫等极端恶劣条件的频发,使人们不得不反思攫取能源的传统方式是否过于粗暴。鉴于此,人们把目光投向了可再生能源,太阳能因其对环境友好、获取便利、转化高效、储量丰富、使用安全等诸多原因,成为人们最为关注的新能源。
在此背景下,全球光伏发电产业增长迅猛,产业规模不断扩大。通过最近十余年的极力发展,2013年光伏全球新装机容量已达38.4 GW,累计达139 GW,在所有新能源发电新增装机容量中占32.4%,位列第一[1]。我国光伏发电装机总容量已达22.42 GW[2]。然而电站面积毕竟有限,太阳能又具有能量密度低的缺点,如何在有限的空间内更有效地设计光伏组件,使其发电量达到最大,提高单位空间有限成本内的发电量,才是我们更应关注的焦点。随着光伏装机规模的不断扩张,电站的可靠和高效运营显得格外重要,其实看似简单的光伏组件才是光伏电站最核心部件,也最易受外界影响——倾角遮挡、风吹雨淋、日久积灰等不利因素都可随时干扰光伏发电,降低发电量,尤其是无法人为改变的气象因素的影响。因此,研究这些影响因素势在必行。
1 评估数学模型
我国疆域广袤,地理差异迥然,气候千差万别,太阳能资源各不相同。为简化数学模型,此处仅考虑太阳直射情况下的日照辐射。
当光伏组件水平放置时,太阳照射到组件上的辐射能为:

式中,Z为地球表面的天顶角;E为太阳光入射的辐射通量密度(此处不考虑大气散射和地面反射的情况,仅讨论垂直入射的平行光束)。
当光伏组件倾角放置时,照射在倾斜组件上的辐射能[3]为:
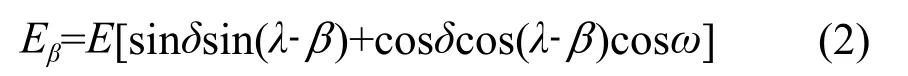
式中,β为组件与水平面的倾角;δ为太阳赤纬角;λ为地理纬度;ω为太阳时角。

式中,n为一年中的天数,一年往返回到原点;δ的范围为 -23.45°~23.45°[4]。
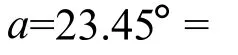
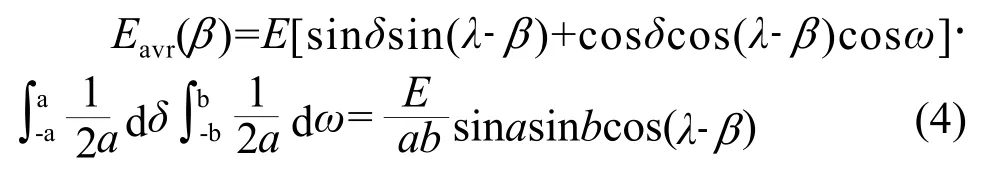
为求出每小时平均日照辐射的最大值,对式(4)求导得:

令式 (5)等于零。因 a≠0、b≠0 、E≠0,则sina≠0、sinb≠0 ,即 sin(λ-β)=0,可得:

式(6)表明当光伏组件和水平面倾角等于当地纬度时,发电量最大,相应年平均日照辐射强度最大。此时每小时平均日照辐射为:

因为年平均日照时间为12 h,则年平均每天日照辐射为[5]:
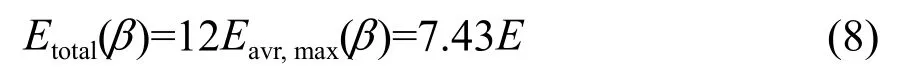
通过以上计算可建立较简单模型,计算每天、每月、每年度理想发电量。如考虑气候差异、大气散射、地面反射等情况,β应根据实际情况在当地纬度基础上于±5°~10°[6]范围内波动。
2 气象数据库建立
太阳能在一年中不同季节、不同月份、不同时间的辐射强度和总量都在不断变化。即使相似时间段,因气象条件不同,光伏组件接收到的辐射强度和总量也有很大区别。这是和上述理论模型的差别所在。因此,实际建站应用时,光伏发电系统会根据负载特性的不同,选择季节性或全年发电量最大的光伏阵列布置方式[7]。尽管一些光伏电厂会采用自动追日系统,可使发电量提高20%~30%,但由于支架成本及运行维护成本的大量增加(1~2.5倍甚至更高)[8],在一定程度上限制了这种方案的推广。因此,本文尝试分析固定倾角铺设方案,以青岛即墨站数据为研究对象建立分析数据库,得到理论平均日辐射、实际平均日气温、具体天气等气象参数和实际发电量之间的关系(见表1),因为是同一光伏电站的数据,因此可排除纬度、海拔、倾角、系统、元器件等不同造成的差别。月发电量和月平均日发电量数据采自笔者公司光伏数据中心,晴、多云、雨雪天数及月平均日气温采自中国气象网数据库,月平均组件安装面日辐射采自NASA数据库。
3 气象条件对发电量的影响
月发电量柱状图如图1所示,可知理论和实际月发电量都呈规律的起伏状态,理论月发电量同一年度内近似于浪形曲线。发电量从每年2月起开始攀升,4、5月时到达波峰,而后开始缓降,7月开始平缓,从10月开始继续下滑至次年1月,循环往复,呈季节性变化。若简化数据样本,以一年为基准按季度分类,得到图2。由此可更清楚地看出春季发电量明显高出其他3季。

图1 月发电量柱状图
即墨站位于山东半岛西南,北纬32°,具有明显的温带季风气候,春季气候干燥、气温回暖且日照时间变长,夏秋两季多雨少晴,冬季日照时间短,可见其余3季相较于春季,气象条件均明显不足。太阳辐射强度具有季节性规律变化,所以导致发电量在趋势上也呈相同变化。作为并网电站,不必考虑发电量的平稳性,如果要提高全年发电总量,应充分利用最优时间段,在高效时尽可能地发电。

表1 即墨站光伏系统气象数据库

图2 季度发电量柱状图
对于同一电站,组件设计倾角、系统元器件选型、海拔纬度等因素完全一致,那么对年发电量影响最大的可能是气候条件。对图1相同时间段的气温情况分析得到图3。两图对比发现,两者有类似的起伏形态,区别仅在于月平均气温的振幅更大。空气温度取决于太阳辐射强度,光伏组件的发电量同样取决于太阳辐射强度,那么空气温度和发电量间是否也存在某种联系呢?

图3 月平均气温图
JIS发电量预测方法中对此做出了回答,JIS各月系统发电量为:

式中,GS为标准条件下日射强度,即式(1)和式(7)中的E,取值为常量1 kWh/m2;HAM为月累计倾斜面日射量;PAS为标准太阳电池板输出能量;K为综合设计系数。

式中,KPT为温度修正系数;K′为基本设计系数。
式中,αPmax为最大输出功率温度系数(晶体硅组件:-0.40~-0.50%/℃);TCR为平均太阳电池模块的温度。

式中,ΔT为太阳电池模块的温度上升调整值;TAV为月平均气温。
把式(12)依次带入式(9)~(11)中,得到月平均气温同月发电量之间的关系:

由式(13)可知,月平均温度TAV与温升ΔT的代数和(太阳能组件TCR)同发电量EPM间存在线性关系。假设其余参考量恒定,仅存在变量TCR,可得组件温度和发电量间关系曲线如图4所示。由此可知,在不考虑其他参考量的情况下,太阳能组件温度越高发电量越小。月平均温度由低到高依次为:冬季、春季、秋季、夏季(见图3)。仅考虑温度一项,冬春两季发电量较大,但由于即墨站位于北回归线以北,冬季日照时间最短,故春季才是发电量最大的季节,和之前结论相符。

图4 温度-发电量曲线
NASA推导出的理论平均日辐射和实测平均日发电量之间的关系如图5所示。
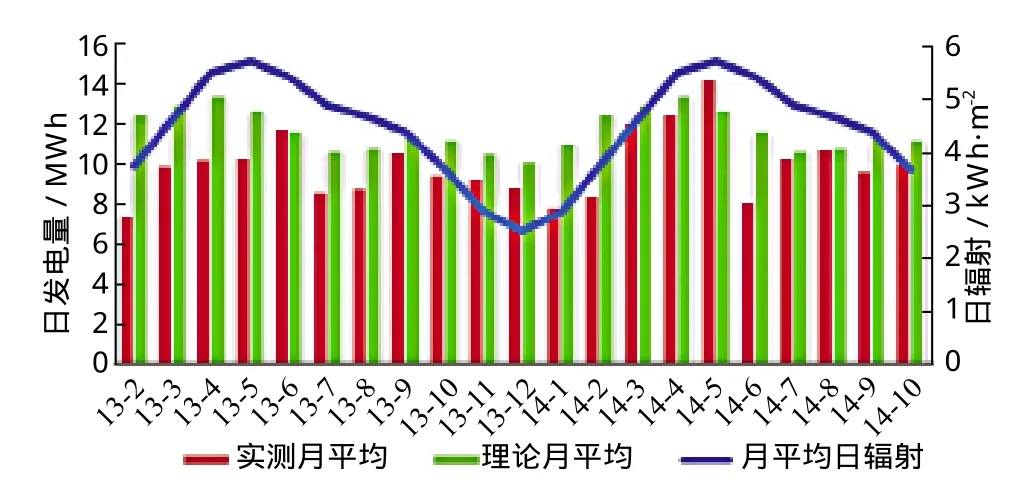
图5 平均日辐射-平均日发电量对比图
由图5可知,理论月均日发电量的起伏和理论月均日辐射曲线完全一致,理论平均日辐射起伏和实际平均日发电量曲线大致相同,理论和实测基本吻合。辐射强度越大发电量就越大。但13-7和14-6两处不相符值得关注,发电量陡然下降,可辐射曲线却较为平缓。为探寻实测和理论的矛盾所在,需具体分析天气情况。
对于组件接收太阳辐射而言,天空云量是其最直接的影响,鉴于此,我们可把各种天气情况按气象定义进行简单分类,如图6所示。

图6 3种天气分布图
在这3大类中,有两个极端项是晴和雨雪。虽然这两项所占天数很少却极其关键,一个是辐射强烈至极,一个是辐射忽略不计。相对而言,多云天气反倒是最为普通常规的现象,对分析发电量暂时不具备特殊意义。故我们将多云天气排除在外,晴雨比例图如图7所示。

图7 晴雨比例图
在图7中寻找图5对应曲线奇点处。13-7处无晴天,却有20个阴天,占据了全月时间的64.5%,再次对应图1的发电量,也解释了当月发电量骤然下降的原因。14-6处也是同样的原因,全月无晴天,11个雨天,占据了全月时间37%。查看数据库中21个月的样本,只有这两个月是雨雪天气超过1/3时间,同时无晴天。晴雨两种极端天气对发电量的影响也类似。但这也是综合了30天的平均情况,其余月份数据中同样也有晴雨两种天气的分布,却未像这两个奇点月显现的如此明显,那么我们抽取具体几天,分析对组件发电量的影响。
图8表示了相近两段连续时间,每段时间都取3天为样本,重点观察两个极端天气的发电量。2014-09-23为晴天,日发电量达到15010.9 kWh,而2014-09-28为全天中小雨,日发电量仅为1406.6 kWh。相近的两天,其余条件几乎完全相同,差别为天气情况,从柱状图中很明显地看出,晴天的发电量几乎是雨天的11倍。
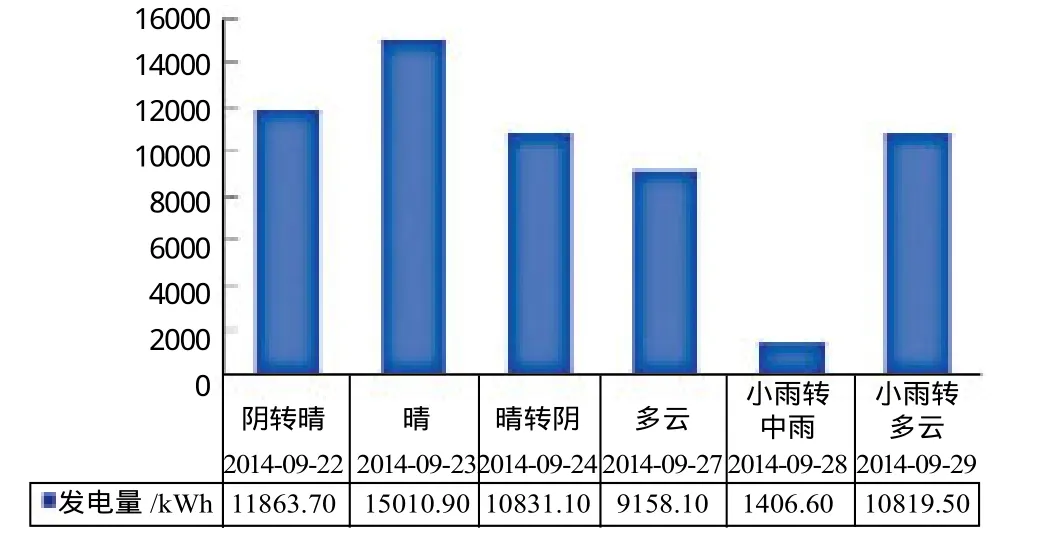
图8 单日发电量柱状图
为避免抽样的特殊性,我们将2014年雨季(7~9月)中所有晴天和雨雪天抽出,做图9以便比较。样本数量增加后对比更加明显,晴天时日发电量均在15 MWh以上,而雨天时发电量基本维持在5 MWh以下,晴天发电量为雨天的3倍。相较于图8,雨天发电量较大。究其原因,图8中,我们为了更好比较选择全天下雨,发电量自然很小,而图9中的雨天并非全天下雨,故而发电量有所提升。无论哪种样式,具体天气的影响或天空中云量对光伏发电的影响都很大。

图9 7~9月份晴雨发电量
4 结论
在光伏系统前期进行发电预测评估时需考虑的因素很多,如光伏阵列倾角、转换效率、太阳光辐射强度、当地气候环境,以及其他一些因素,都会对光伏阵列的发电量产生影响。对于既定光伏系统来说,所有数据都自于同一套系统,因此采用历史发电数据来进行评估待建光伏电站的发电量,比间接评估预测具有明显的准确性和必要性。尤其是类似即墨站,采用屋顶铺设组件,并选择了最佳倾角固定安装,当人为条件都已最优化后,愈发显得气象条件的重要。本文使用了即墨站的既有数据,通过和NASA推导数据进行综合测评,分析了平均日辐射、阴晴天气、平均温度与光伏发电量之间的关系。由于样本较为单一,在今后的工作研究中有待进一步充实数据,完善方案。
[1] European Photovoltaic Industry Association. Market& competitiveness [EB/OL]. http://www.epia.org/policies/sustainable-market-development/market-competitiveness/.
[2] 吴新雄. 携手通向未来的亚太可持续能源发展之路[R].亚太经合组织第十一届能源部长会议, 北京, 2014.
[3] 王炳忠. 相对于斜面的太阳位置计算[J]. 太阳能, 1999, (3):8-9.
[4] 日本太阳能学会. 太阳能的基础和应用[M]. 上海:上海科学技术出版社, 1982.
[5] 吴少波. 光伏阵列年最大发电量固定倾角的确定[J].太阳能, 2011, (5): 27-29.
[6] 杨金焕, 葛亮, 陈中华, 等. 季节性负载光伏方阵的倾角[J].太阳能学报, 2003, 24(2): 241-244.
[7] Tsalidesa P, Thanailakisa A. Direct computation of the array optimum tilt angle in constant-tilt photovoltaic systems [J]. Solar Cells, 1985, 14(1): 83 - 94.
[8] 叶东嵘. 平单轴自动跟踪系统简介[A]. 北京市计科能源开发新技术开发公司, 太阳能光伏发电技术与优化设计交流会[C], 北京, 2011.

