工业机器人笛卡尔空间轨迹规划

林 威，江五讲

（华中科技大学 机械科学与工程学院，湖北 武汉 430074）

0 引言

在机器人笛卡尔空间规划系统中，作业是用末端位姿的齐次变换矩阵序列规定的，轨迹规划就是根据描述的作业计算出运动的位移、速度和加速度，生成运动轨迹［1］。工业机器人的轨迹规划既可以在关节空间也可以在笛卡尔空间中进行，但是轨迹曲线都必须平滑，以保证机器人运行平稳。关节空间的轨迹规划相对简单，但是其末端的运动轨迹不直观；笛卡尔空间的轨迹规划不仅概念上直观，而且规划的路径准确，可以清晰地观测到末端执行器的运动轨迹［2，3］。目前工业机器人使用的最广泛的方法是示教再现，也就是根据任务的需要，记录轨迹上一些关键点，而要想使末端执行器严格地按照所要求的轨迹运动，则必须取得足够多的点。机器人的运动轨迹一般都是圆弧或者直线，复杂的运动轨迹一般用直线和圆弧对其拟合而得到，这是机器人实现复杂运动轨迹的关键［4，5］。本文提出了利用抛物线过渡的空间直线插补算法和基于局部坐标系的空间圆弧插补算法，保证了实验室自行设计的五自由度喷涂机器人运动的平稳性。

1 基于抛物线过渡的空间直线插补

直线的轨迹规划是已知直线的起点和终点的位置和姿态，求解直线轨迹上插补点的位置和姿态，并保证机器人位置及姿态平稳过渡。

假设机器人末端由P1点沿直线运动到P2点，（x1，y1，z1）和（α1，β1，γ1）分别为起点P1的位置和RPY角，（x2，y2，z2）和（α2，β2，γ2）分别为终点P2的位置和 RPY 角，（xi，yi，zi）和（αi，βi，γi）分别为中间插补点Pi的位置和RPY角，如图1所示。

各插补点的位置和姿态可由公式（1）求出：

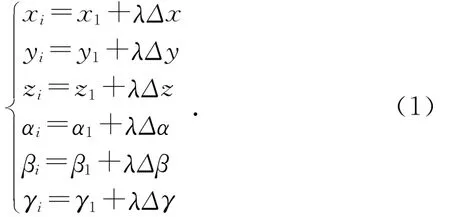
其中：λ为归一化因子；Δx，Δy，Δz，Δα，Δβ，Δγ为位置和RPY角的增量，其求解如下：

λ归一化因子采用抛物线过渡的线性函数，以保证整段轨迹上的位移和速度都连续。抛物线过渡的线性函数是对两点的位姿使用线性插值时，在两点的邻域内增加一段抛物线的缓冲区段。假设两端的抛物线运动时间相等，即在两个过渡区域中的加速度值相同、符号相反。设λ′为λ对时间的导数，λ′随时间t变化的曲线如图2所示。

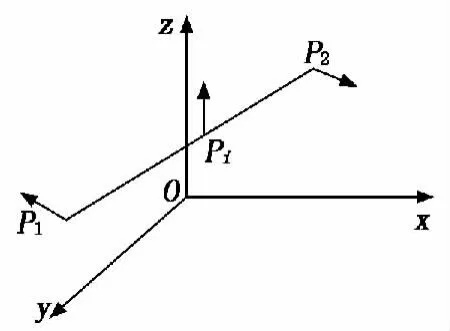
图1 直线运动示意图

设直线段的速度为v，抛物线段的加速度为a，那么抛物线段的运动时间Tp和位移Lp分别为：

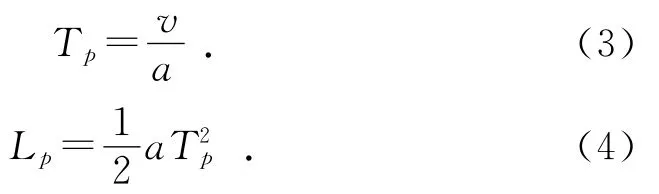
直线运动总位移和时间分别为：

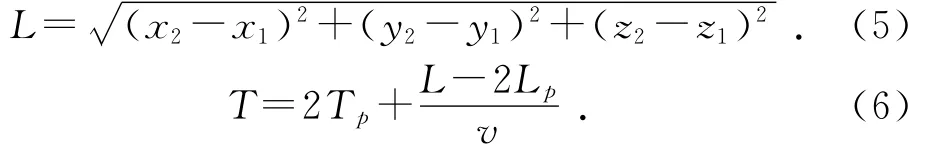
对抛物线段的位移、时间、加速度归一化处理得：

则λ的计算公式为：

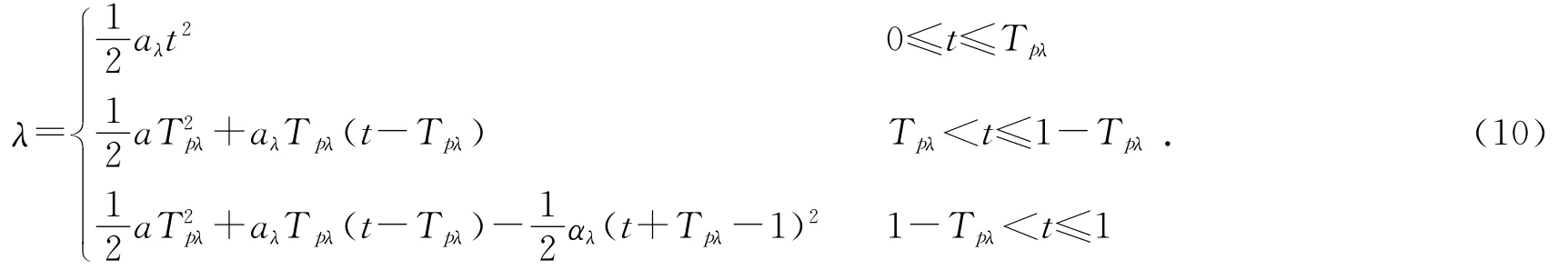
其中：t＝i／N，i＝0，1，2，…，N，N为插补点个数，i＝0代表起点，i＝N代表终点。将所求λ代入式（2）即可求得各插补点的位置和姿态。求得各插补点的位置和姿态后，再通过运动学反解，可以得到各插补点对应的关节角度值。

图2 λ′随时间t变化的曲线

2 基于局部坐标系的空间圆弧插补

假设机器人末端执行器从起始位置P1经过中间点P2到达终点P3，若这3点不共线，则一定存在从P1经P2到P3的圆弧。按照以下步骤进行空间圆弧的轨迹点位置的插补，如图3所示。

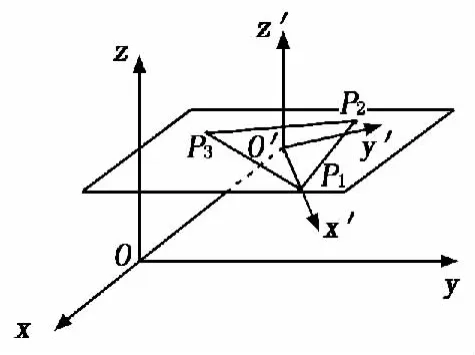
图3 坐标系与局部坐标系

（1）求圆心坐标P0（x0，y0，z0）及半径R。由P1（x1，y1，z1），P2（x2，y2，z2），P3（x3，y3，z3）三点可确定平面，得方程：

根据圆心到三点的距离都为半径可列出下列方程：

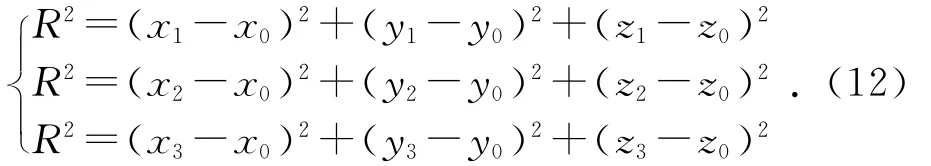
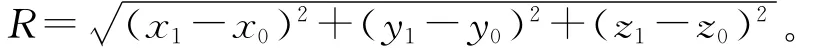
（2）建立圆弧所在平面的新坐标系。取圆心P0为新坐标系原点O′，P0P1方向为x′轴方向，其单位方向向量为：

P1P2和P2P3决定圆弧所在平面，取垂直于此平面的方向为z′轴，其单位方向向量为：

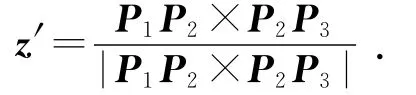
根据右手法则，y′轴的单位方向向量为：

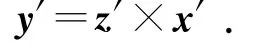
用齐次变换矩阵TR描述新坐标系O′－x′y′z′相对于原坐标系O－xyz的位姿，则：

（3）将P1，P2，P3，P0从原坐标系O－xyz变换到新坐标系O′－x′y′z′。设P1，P2，P3，P0在原坐标系O－xyz中的坐标值分别为（x1，y1，z1），（x2，y2，z2），（x3，y3，z3），（x0，y0，z0），在新坐标系O′－x′y′z′中的坐标值分别为（x′1，y′1，z′1），（x′2，y′2，z′2），（x′3，y′3，z′3），（x′0，y′0，z′0），则：

由建立的新坐标系O′－x′y′z′可知：x′0＝y′0＝z′0＝0，z′1＝z′2＝z′3＝0，x′1＝R。

（4）在新坐标系O′－x′y′z′上进行圆弧插补。设圆弧上一点p在O′－x′y′z′中的坐标为（x′，y′，z′），对应的归一化因子为λ，从P1到p的角度为θ，从P1到P3的角度为θ′，则：

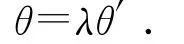
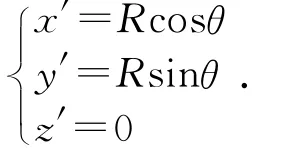
（5）将新坐标系上的插补点的值转换到原坐标系中。设点p在原坐标系O－xyz中的坐标值为（x，y，z），对应的p′在新坐标系O′－x′y′z′中的坐标值为（x′，y′，z′），则：

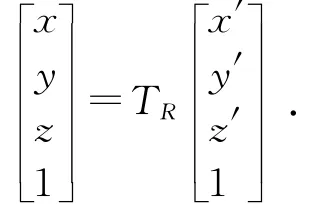
根据以上步骤，可以得到圆弧上各插补点的位置。各插补点的姿态可由下面方程求出：

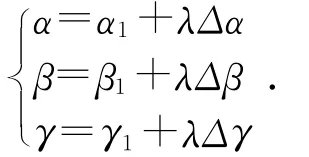
求得各插补点的位置和姿态后，再通过运动学反解，可以得到各插补点对应的关节角度值。

3 实验分析

以实验室自行设计的五自由度喷涂机器人为实验平台，验证以上算法。该机器人结构示意图如图4所示。

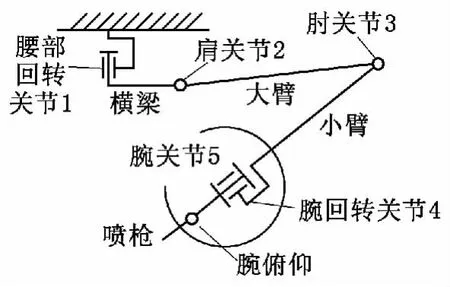
图4 喷涂机器人结构示意图

对于直线运动，给定机器人末端起点、终点对应的关节角度；对于空间圆弧运动，给定机器人末端起点、中间点、终点对应的关节角度，通过运动学正解求出两点对应的位姿矩阵，然后采用前面提出的轨迹规划算法进行插补运算，得到各插补点的位姿，最后通过运动学反解，求得各插补点对应的各关节角度。通过示教的方式进行实验，由轨迹规划得到的结果画出各关节角度变化图，设定运动为一段空间直线P1P2、一段平面圆弧P2P3P4、一段空间圆弧P4P5P6，如图5所示，得到的各关节角度随时间的变化如图6所示。图6中，θ1，θ2，θ3，θ4和θ5分别对应图4中关节1、关节2、关节3、关节4和关节5的角度。

根据以上实验分析可知，按照示教的轨迹，采用基于抛物线过渡的空间直线插补算法和基于局部坐标系的空间圆弧插补算法，使实验五自由度喷涂机器人成功按照要求的轨迹进行运动，且运行平稳，轨迹衔接平滑。

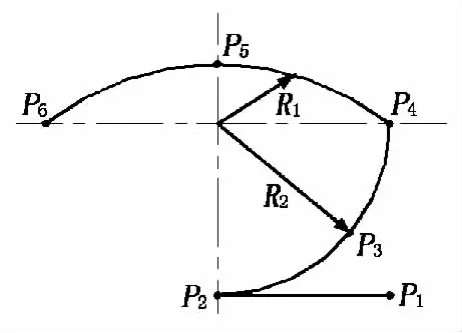
图5 设定的运动轨迹图

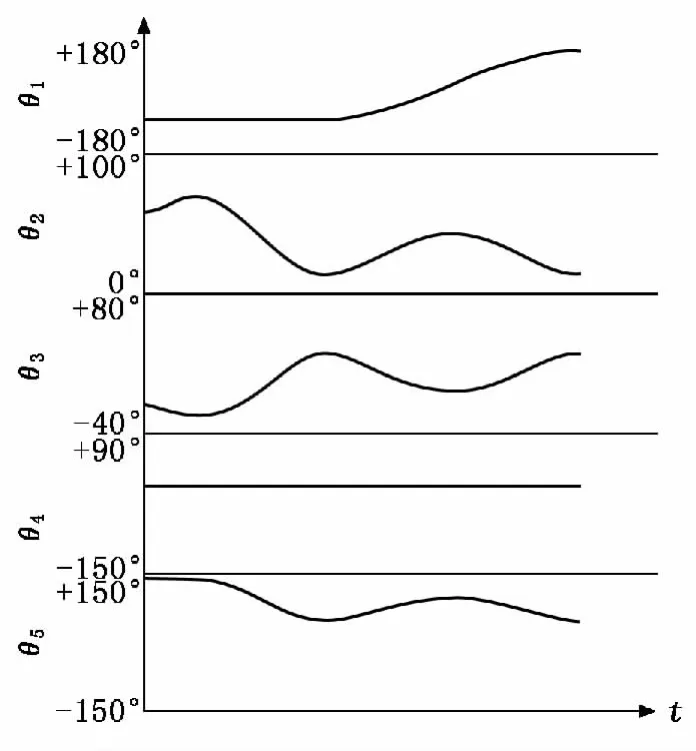
图6 各关节角度随时间变化图

4 结束语

空间直线和圆弧的轨迹规划算法是最基础的算法，已经广泛应用于工业机器人中。以自行设计的五自由度喷涂机器人为实验平台，通过示教的方式，记录一系列离散的关节角度，再通过机器人运动学正解，求出这些点对应的末端执行器的位姿，在笛卡尔空间中，根据设定的运动进行轨迹规划，计算各插补点的位姿，再通过机器人运动学反解，将这些插补点的位姿反解为关节角度，最后由这些关节角控制机器人末端执行器沿着规划的轨迹运动。由于采用了基于抛物线过渡的空间直线插补算法和基于局部坐标系的空间圆弧插补算法，保证了机器人的运动平稳、平滑。

［1］ 熊有伦.机器人技术基础［M］.武汉：华中理工大学出版社，1996.

［2］ 卢君宜，杨庆华，高峰，等.五自由度农业采摘机器人轨迹规划［J］.机电工程，2010（12）：1－6.

［3］ 张凯，刘成良，付庄，等.6R机器人轨迹规划及其在焊接中的应用［J］.机械设计，2002（10）：20－23.

［4］ 王悦善，陈曾汉.嵌入式数控系统实时插补加减速控制算法研究［J］.煤炭技术，2012（2）：25－26.

［5］ 王卫忠，赵杰，高永生，等.机器人的平面曲线轨迹规划方法［J］.哈尔滨工业大学学报，2008（3）：389－392.