混合励磁同步电机低速大力矩控制策略的研究❋

冯 杰，李优新，黎 勉，王胜强，杨 宾

（广东工业大学，广东 广州 510006）

0 引言

混合励磁同步电机（hybrid excitation synchronous motor，HESM）在结构、性能方面与永磁同步电机（PMSM）有相似之处，但其驱动与控制有其特殊性。东南大学黄明明博士给出了混合励磁同步电机分区控制系统［1］。日本学者Shinji Shinnaka建立了一种基于通用坐标系的动态矢量控制模型及对隐极HESM提出了一种基于转子磁场定向的铜耗最小化矢量控制模型［2，3］。广东工业大学的李优新博士提出了一种混合励磁无刷直流电机的控制策略［4］。本文针对一台额定功率为6kW的HESM，基于空间电压矢量（Sector Voltage PWM，SVPWM）控制的思想，在传统的PMSM驱动器模型上加入了一个电流分配器，通过电流分配器合理分配电枢电流与励磁电流之间的关系，实现电枢电流与励磁电流之间的解耦，实现HESM驱动器的可靠稳定工作。

1 HESM的结构原理与驱动系统模型

1.1 HESM的结构

图1为HESM内部结构示意图，电机的定子与普通的PMSM定子相同。从电机的电磁关系来看，HESM与PMSM相比，结构上多了励磁绕组［5］。

1.2 调磁机理

当不加励磁电流时，励磁绕组不产生励磁磁势，则电机气隙中只有永磁磁通，此时的HESM就相当于一台PMSM。如图2所示，当负载力矩超过电机额定力矩，则向HESM的励磁绕组中通入增磁励磁电流。电机气隙中将产生与永磁磁通ΦPM方向相同的励磁磁通Φf，以达到增加电机磁通的效果。电机磁通增加后，使得电机在不增加电枢电流的前提下增大了电机的输出力矩。

图1 HESM内部结构示意图

1.3 HESM的驱动系统模型

不失一般性，对于这台HESM，忽略HESM的电枢电压、电流谐波分量等的影响，仍然采用dq坐标系来建立HESM驱动系统模型。根据SVPWM的控制原理，可得到HESM的控制系统模型，如图3所示。HESM驱动系统的主要功能模块与传统的PMSM驱动系统相比，主要是控制对象不同并且多了3个模块，分别是励磁电流脉宽调制信号、励磁驱动及电流分配器。其中的电流分配器是最为关键的一部分，它是被用来合理分配电枢电流与励磁电流之间关系的，以保证HESM的稳定与可靠运行。

HESM电流分配器的结构框图如图4所示，HESM驱动器通过电流分配器调节q轴电流参考值与励磁电流参考值。由于采用Id＝0的矢量控制，所以d轴电流参考值在驱动系统中直接赋为零值。通过电机旋转角速度ωr、驱动器的母线电压Udc两变量来选择控制区域。当负载力矩没有超过电机的额定力矩时，电机运行在常规力矩区，此时的驱动器就相当于一台PMSM驱动器。当负载力矩大于电机额定力矩时，电机进入动态增磁区，HESM驱动器通过增加以达到增大电机输出力矩的目的。驱动系统通过一个旋转编码器获得电机的ωr与电角度θ；电机转速参考值由驱动器给定；Tref为电机参考输出力矩。

图2 电机定、转子截面图

图3 HESM驱动系统模型

图4 HESM电流分配器结构框图

2 HESM的低速大力矩控制策略

2.1 总体控制思想

本文提出一种简单有效的控制算法，即当负载力矩在HESM额定力矩以下时，HESM不用增加励磁电流，即if＝0，此时的HESM可以看作一台PMSM，可以采用传统的PMSM控制策略；当负载在额定力矩以上时，保持HESM原有电枢电流值不变，调节HESM的励磁电流if，从而增加励磁磁通使得HESM的输出力矩与负载力矩之间的动态平衡，在不增加电枢电流的前提下实现HESM的低速大力矩的特性。

2.2 低速大力矩控制算法

下面来推导HESM在动态增磁区时，电枢电流与励磁电流的基本关系。设Te为电机的输出力矩：

其中：p为极对数；iq为q轴电流；ψpm为永磁磁链；Lsf为电枢绕组与励磁绕组之间的互感；if为励磁电流的瞬时值。设TeN为电机在不加励磁电流情况下的额定输出力矩，则：

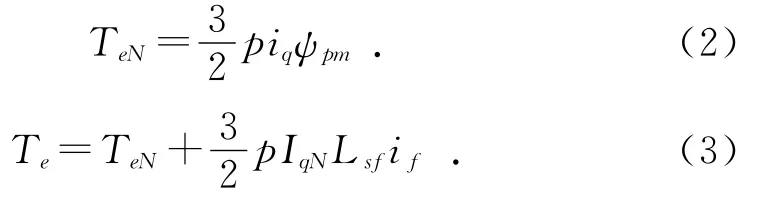
其中：IqN为q轴电流额定值。根据式（3），可以推算出：

令

iTref为当负载力矩大于TeN时所需的力矩对应的q轴电流值，则Te－TeN之间的差值由励磁电流来补充。

由式（2）、式（4）、式（5）可得：

HESM转子在旋转坐标系下，定子绕组与励磁绕组磁链方程为：

其中：ψd，ψq分别为电机的d轴与q轴的磁链；ψf为励磁绕组的磁链；Ld，Lq分别为电机的d轴与q轴自感系数；Lf为励磁绕组自感系数；id，iq分别为d轴与q轴的瞬时电流值。将式（7）展开，再根据ψ与U的关系式，可得：

其中：ud，uq分别为电枢电压d，q轴值；uf为励磁绕组电压值；Rs为定子绕组电阻值；Rf为励磁绕组电阻值；ω为电机同步角速度。

其中：nN为电机转速额定值。在电机进入恒功率区后，Ifmax要小于等于励磁电流额定值IfN；同时，其最大励磁电流Ifmax又不能超过。所以有：

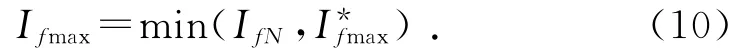
当IfN＝max时，则由式（9）可知，此时电机转速为：

则由式（8）、式（10）可得，当电机转速n＊≤n1时，Ifmax＝IfN；当n＊＞n1时，Ifmax＝，HESM在n1～nN这段速度区间内为恒功率区，会随着电机转速的增加而减小。

动态增磁区的工作流程可以总结为：当负载力矩大于电机输出力矩时，导致电机转速下降，转速环对电流分配器的给定电磁力矩参考值增加。电流分配器根据力矩参考值在if＝0的模式下计算出iq，再保持iq＝IqN；通过式（6）计算出if，再根据式（9）、式（11）得出if的最大值Ifmax。通过增加if使得输出力矩加大，实现电机力矩与负载力矩间的动态平衡。

3 实验分析

实验以一台额定功率为6kW、频率为50Hz的8极HESM为对象，实验数据由泰克公司的DOP3000型示波器采集，由OriginLab处理后所得。HESM样机的力矩和转速数据由日本小野公司的TS-3100数字力矩仪测得。实验用HESM基本参数见表1。

图5是在转速为1 600r/min、励磁电流为10A，负载力矩发生突变时，HESM的动态响应图。由图5可看出：当负载力矩由15N·m突变到25N·m时，转速出现微小的下降，但又很快恢复到额定转速；当负载力矩由25N·m突变到15N·m时，转速出现了上升，但很快恢复到额定转速。故HESM驱动器具有良好的动态响应性能。

表1 实验用HESM基本参数

图6为当HESM分别在转速为500r/min、1 500 r/min、2 500r/min，电机电枢电流维持不变时，电励磁电流不断增加时电机的输出力矩，可以看出输出力矩也呈线性增加。

实验结果表明，HESM通过增加电机励磁电流，增大电机磁通，使得电机在电枢电流不变的前提下获得更大的输出力矩，提高了电机的帯载能力。

4 结论

本文针对HESM的特点，提出的新型低速大力矩控制策略具有如下特性：在动态增磁区，实现了电枢电流与励磁电流的自然解耦，大大降低了控制算法的复杂性，使算法的软件化更为简单可行；在增加了励磁电流之后，HESM相对于传统的PMSM，输出力矩有较大的提升，实现了低速大力矩的特性；驱动系统具有非常好的稳态性能，在额定转速时，能够提供较相同的PMSM更大的力矩。

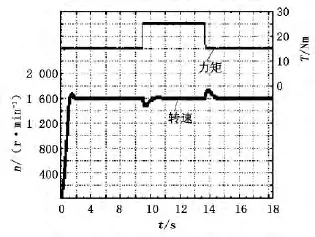
图5 HESM的动态响应图

图6 HESM在不同励磁电流下的输出力矩

［1］黄明明，林鹤云，金平，等.新型混合励磁同步电机分区控制系统分析与设计［J］.中国电机工程学报，2012，32（12）：120-125.

［2］Shinnaka S.New dynamic mathematical model and new dynamic vector simulators of hybrid-field synchronous motor［C］//IEEE International Conference on Electric Machines and Drives.San Antonio，TX，USA，2005：882-889.

［3］Shinnaka S，T Sagawa，New optimal current control methods for energy-efficient and wide speed-range operation of hybrid-field synchronous motor［J］.IEEE Transactions on Industrial Electronics，2007，54（5）：2443-2450.

［4］李优新.混合励磁无刷直流电机的结构及控制策略研究［J］.微特电机，2003，31（3）：3-5，37.

［5］叶斌英，阮毅，杨勇，等.基于混合励磁电机的直驱式风电系统［J］.电机与控制应用，2010，37（5）：1-6.