3-RRR并联机构灵巧度分析

杜聿静，王 雷

（潞安职业技术学院，山西 长治 046204）

0 引言

当一并联机构处于奇异位形时，经计算可得出，该机构此时的雅可比矩阵为零或者趋于无穷大，这意味着该机构被刚化或者存在多余的自由度，此时机构的运动不能唯一确定，因此，机构应在实际操作中尽量地避免奇异位形。理论上讲，当并联机构的位姿接近奇异位形时，机构的雅可比矩阵会成为病态矩阵，继而造成机构逆矩阵的精度降低，这种衡量机构运动失真程度的指标称为灵巧度。并联机构的灵巧度属于一种运动学性能指标，它是用来描述机构输出运动（力）与输入之间的失真程度，同时还可以定量衡量机构远离奇异点的程度。雅可比矩阵的条件数、可操作数则是衡量并联机构灵巧度的常用指标。本文主要利用可操作数和条件数来对3-RRR并联机构进行灵巧度分析。

1 3-RRR并联机构三维模型的建立

SolidWorks软件是世界上第一个基于Windows开发的三维CAD软件系统。功能强大、易学易用和技术创新是SolidWorks软件的3大特点，这使得SolidWorks软件成为领先的、主流的三维CAD解决方案。由于SolidWorks软件能够提供多种不同的设计方案、极大地减少了设计过程中的错误，因而Solid-Works软件也成为机械设计行业中应用最广泛的三维建模软件之一。

首先利用SolidWorks软件建立出3-RRR并联机构的三维模型，如图1所示。该机构由3个相互并联的分支、静平台和动平台3部分构成。其中每个分支又由3个转动副串联而成，而且每个分支的结构和杆长完全一致。3个高度等各项参数完全一致的固定铰支座构成了3-RRR并联机构的静平台。3个分支下端分别铰接在静平台上，分支的另一端则铰接在三角形的动平台上。

图1 3-RRR并联机构模型

2 建立空间坐标系并计算各运动螺旋

根据所建立的三维模型，采用D－H法建立3-RRR并联机构的空间坐标系。当该机构处于任意位姿时，选取任一固定铰支座的旋转中心如点A为原点，点A与另外两个铰支座旋转中心点G、点D的连线AG、AD分别为x和z轴（AG⊥AD），垂直于3个固定铰支座所在平面且过点A的直线为y轴；同时假设与静平台相铰接的3个连杆均垂直于DOG面，与动平台相铰接的3个连杆均相对于铅垂线偏移同样的角度，故而，动平台与静平台在运动过程中一直保持着互相平行的关系，而且将动平台和静平台上的各铰接点分别连线后形成的两个三角形CFI和AGD为全等的直角三角形。由此，我们建立出该并联机构的空间坐标系［1］，如图2所示。

根据螺旋理论公式计算机构的各螺旋：

其中：＄n为螺旋，n＝1，2，…，9；Sn为螺旋轴线的方向矢量，为螺旋的原部；S0n为螺旋轴线的位置矢量，为螺旋的对偶部。

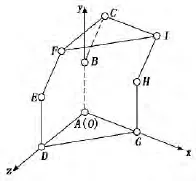
图2 3-RRR机构坐标系

通过式（1）可计算出并联机构的各螺旋为：

A点：＄1＝［0 0 1；0 0 0］，

B点：＄2＝［0 1 0；y20x2］，

C点：＄3＝［0 0 1；y3－x30］，

D点：＄4＝［0 0 1；0 0 0］，

E点：＄5＝［0 1 0；－z50 0］，

F点：＄6＝［0 0 1；y6－x60］，

G点：＄7＝［0 0 1；0 －x70］，

H点：＄8＝［0 1 0；0 0x8］，

I点：＄9＝［0 0 1；y9－x90］.

从而可得出3-RRR并联机构的运动螺旋系为：

3 求解机构任意位形时的雅可比矩阵

运动雅可比矩阵也可称为一阶运动影响系数矩阵，通过以下步骤进行计算［2］。

（1）根据公式（2）求出平台转动对分支运动副变量的一阶偏导影响系数矩阵［GhΦ］：

其中：Sn可直接引用前面的结果。该机构为全转动副，由此可得：

（2）取FI的中点为P点，如图3所示。设Rn为机构上各铰点的坐标，根据公式（3）求出平台移动对分支运动副变量的一阶偏导影响系数矩阵［Gpφ］：

其中：j为运动副的数目。设图3中AD＝AG＝CI＝FC＝a，AC＝FD＝IG＝b，CB，FE，IH与y轴夹角为θ。可得P点的坐标为（0.5a，b，0.5a），R1即A点的坐标为（0，0，0），R2即B点的坐标为（0，0.5b，0），R3即C点的坐标为（0，b，－0.5bsinθ），R4即D点的坐标为（0，0，a），R5即E点的坐标为（0，0.5b，a），R6即F点的坐标为（0，b，a－0.5bsinθ），R7即G点的坐标为（a，0，0），R8即H点的坐标为（a，0.5b，0），R9即I点的坐标为（a，b，－0.5bsinθ）。据此可得：

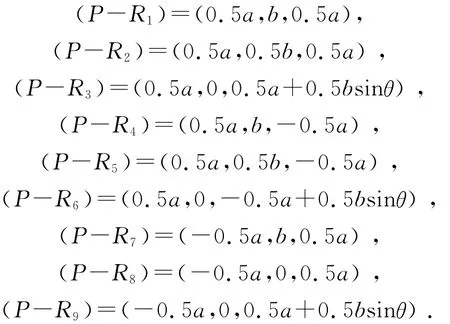
图3 P点位置

该机构为全转动副，由此可得：

（3）根据式（4）求出该机构的一阶运动影响系数矩阵［］，即运动雅可比矩阵J（q）：

4 3-RRR并联机构的灵巧度分析

机构的灵巧度可通过雅可比矩阵的条件数、最小奇异值、条件数的倒数、可操作数等来衡量，本文利用可操作数和条件数对机构进行灵巧度分析。

4.1 利用可操作数w来衡量

可操作数w由下式计算：

其中：σ1，σ2，…，σm为J（q）的奇异值。

若w＝0，则机构奇异；反之若w≠0，则机构不奇异。很明显根据式（4）求得J（q）＝0，再由式（5）可计算得出w＝0，故而该并联机构此时处于奇异位形［3］。

4.2 利用雅可比矩阵的条件数K（J）来衡量

首先要求出雅可比矩阵的奇异值，考虑计算的复杂程度，本文通过求雅可比矩阵的特征值来求解奇异值。经过变换整理可得：

由式（6）可得雅可比矩阵的奇异值σi＝，其中λi为雅可比矩阵的特征值，i＝1，2，…，6，0≤σm≤…≤σ2≤σ1。由于σm＝0，从而可得出｜J（q）｜＝σ1σ1…σm＝0，K（J）＝

条件数的范围是：1～＋∞，当条件数为1时，求逆精度最高；当条件数趋于无穷时，该机构的雅可比矩阵奇异，所以该机构此时处于奇异位形。

5 结论

本文利用SolidWorks软件建立了3-RRR并联机构的三维模型，利用D－H法建立了该并联机构的空间坐标系，并由此利用螺旋理论计算出该并联机构的各运动螺旋，建立运动螺旋系，据此求出该并联机构的运动雅可比矩阵，并对该并联机构的一阶运动影响系数进行分析，求出可操作数和条件数，对机构的灵巧度进行分析。得出分析结果：该机构处于任意位形时，它的雅可比矩阵都必定奇异。同时发现该机构运动时只可以绕y轴和z轴转动，不能绕x轴转动，缺乏一个x方向的自由度。

［1］黄真，赵永生，赵铁石.高等空间机构学［M］.北京：机械工业出版社，2006.

［2］熊有伦.机器人学［M］.北京：机械工业出版社，1993.

［3］杨玉维，赵新华.3-RRRT并联机器人工作空间与灵巧度分析［J］.机械设计，2005（2）：11-13.