一种代理盲多重签名的分析和改进

陈仁群， 左黎明， 汤鹏志

（华东交通大学 基础科学学院，江西 南昌 330013）

盲签名的概念是Chaum在1982年美国密码学会上提出的［1］。一个盲签名方案是用户与签名者之间的一个交互协议。文献［2－3］首先提出了代理签名的概念，文献［4］提出了代理多重签名的概念，使之有了更大的应用。国内外学者相继提出了很多代理多重签名方案，如基于身份的代理多重签名方案［5］和前向安全的代理多重签名方案［6］等。为了实现数字现金和电子商务等［7］活动中的匿名性和不可追踪性，人们将盲签名和代理多重签名方案相结合，提出了盲代理多重签名方案［8－9］。在代理多重签名方案中，经过一个原始签名授权组的授权，被指定的代理签名人可以代表这个签名组生成有效的签名。本文先对一个基于椭圆曲线的代理盲多重签名方案［10］进行安全性分析，再基于双线性配对提出一个安全、高效的代理盲多重签名方案，并对改进方案进行了较为详细的安全性分析。

1 对原方案的回顾及分析

1.1 方案回顾

1.1.1 初始化

系统参数：记作｛D＝（q，a，b，E，G，n，h），H｝，其中，q为有限域的元素个数，有p＝q或q＝2m；Fq为有限域中元素的表示方法；a，b∈Fq，定义Fq上的椭圆曲线：p＞3时，y2＝x3＋ax＋b，或当p＝2时，y2＝x3＋ax＋b；E为Fq上非奇异的安全椭圆曲线；G为E（Fq）的一个点，阶为n；n为一个素数，n＞2160且n＞4；余因子h＝#E（Fq）／n，h≪n，利用h可以较快地找到满足以上条件的基点G；H为一个安全的哈希函数。

1.1.2 委托过程

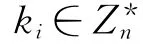
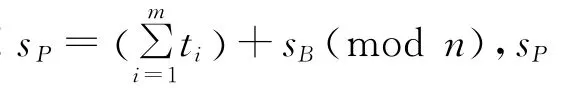
1.1.3 代理盲多重签名的生成

B接到签名请求后，随机选取k∈，计算R＝kG，并把R传给用户U。

U随机选取α，β，λ∈，计算r＝xRmodn，V＝αR＋βG＋λPP＝（xV，yV），u＝xVmodn，c＝H（m‖u）modn，C＝α－1r－1（cu－λ）modn，并将C传给B；B收到C后，计算s＝rCsP－k（modn），并将s传给U。

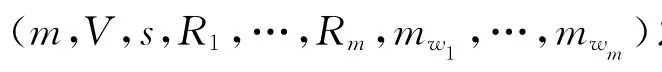
1.1.4 代理盲多重签名的验证

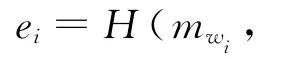
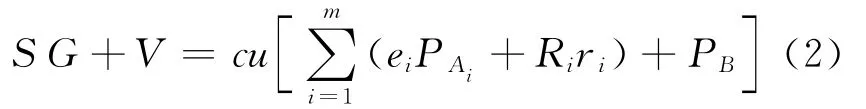
1.2 对文献方案的安全性分析

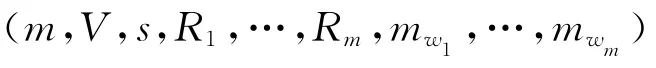
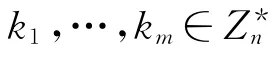
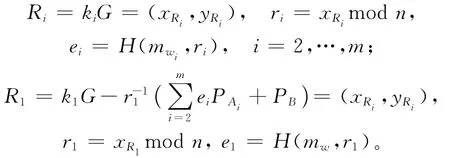
伪造的代理签名密钥为：

相应的代理签名公钥为：

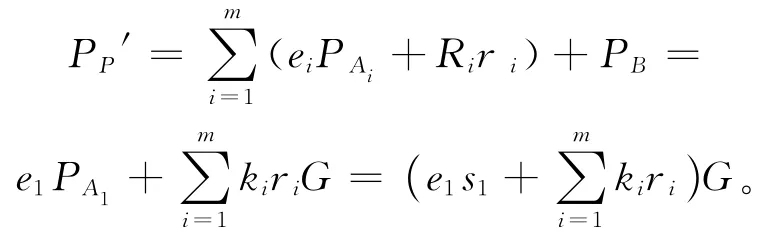
A1完成伪造私钥公钥对后，随机选择k∈，计算），将R传给U。

U随机选取α′，β′，λ′∈，计算：

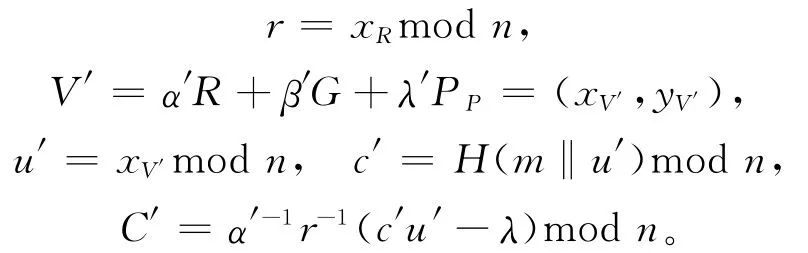
将C′传给A1，A1收到计算s′＝rC′sP′－k（modn），并将传给U。

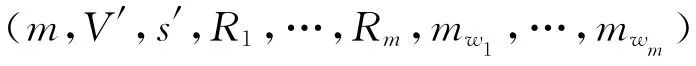
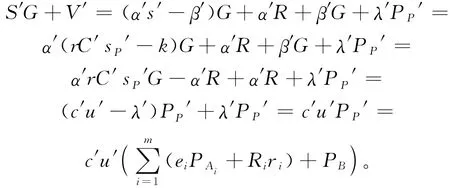
因此，任意验证者可以验证由伪造的sP′产生的代理盲多重签名，即恶意的原始签名A1在没有其他原始签名人和代理签名人参与的情况下，也可伪造出一个代理盲多重签名给任意的验证者验证。

2 改进的代理盲多重签名方案

改进的签名方案是基于双线性配对的，该方案参考了文献［11－13］。

2.1 预备知识

2.1.1 双线性映射

定义1 令G1、G2分别为阶为大素数q的循环加法群和循环乘法群［14］，设P为G1的一个生成元，即G1＝（P）。双线性对是指满足以下性质的一个映射，即e：G1×G2→G2。

（1）双线性。e（aP，bQ）＝e（P，Q）ab，对任意P，Q∈G1，任意a，b∈Zq均成立。（2）非退化性。存在P，Q∈G1，使e（P，Q）≠1。（3）可计算性。对任意P，Q∈G1，存在一个有效的算法计算e（P，Q）。

2.1.2 Gap Diffe－Hellman群

与双线性对有关的数学问题［7］如下：

（1）散对数问题（DLP）。任意给定G中2个元素P、Q，求n∈，使Q＝nP成立。

（2）计算 Diffie－Hellman问题（CDHP）。给定P，aP，bP∈G，其中，a，b∈，计算abP。

（3）判定 Diffie－Hellman问题（DDHP）。给定P，aP，bP，cP∈G，对于a，b，c∈，判定c＝abmodq是否成立。

（4）Diffie－Hellman差距问题。在群G1上CDHP难解而DDHP易解，则称群G1为GDH群。GDH群通常存在于有限域上的超奇异椭圆曲线或超椭圆曲线中，双线性对可由 Weil对或Tate对获得。本文所提出的方案是基于GDH群的，假定G1、G2上的DLP和CDHP都是难解的，并假定双线性对分叉问题是难解的，即给定P∈G1，r∈G2，找到Q∈G1，使r＝e（P，Q）成立是困难的。

2.2 基于双线性对的代理签名方案

2.2.1 系统初始化

本文构造的方案共有以下几类参与者：密钥的分布者、原始签名者、代理签名者和验证者。给定一个秘密k∈，密钥的发布者随机选择P2，P3，…，Pm∈K，令V＝（P1，P2，…，Pm），其中，P1＝k。由矢量空间秘密共享方法［9］可知，秘密k＝c1x1＋…＋cmxm，若有一个授权子集D＝｛A1，…，Am｝存在。其中ci∈K可被任何参与者计算，即任何参与者都能计算出秘密k＝c1x1＋…＋cmxm。秘密发布者通过安全信道为每个原始签名人Ai发布一个秘密作为私钥，并计算其公钥代理签名人B随机选择作为自己的私钥，并公开其公钥yB＝xBP。公布系统参数（G1，G2，P，q，e（·，·），H0（·），H1（·），yB）。

2.2.2 代理签名阶段

（1）原始签名人组Ai，i∈（1，…，m）产生授权证书mw（内含代理授权的有效期限与授权范围、原始签名人组Ai与代理签名人B各自的身份等诸多代理的相关信息），原始签名人组Ai随机选取ri∈，计算Ui＝riP，ti＝H0（mw，Ui）（H0：｛0，1｝×G2→为安全的哈希函数），xi＝，并将（xi，t）发送给代理签名人B。

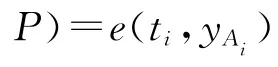
（3）用户U先将需要进行代理签名的消息m盲化，方法如下：先随机选取k∈，计算M＝k－1H1（m）（H1：｛0，1｝→G1为安全的哈希函数），U将得到的M发送给代理签名人B。

（4）代理签名人B接收到M后，计算θ′＝xM，然后将得到的θ′发给用户U。

（5）用户U接收到θ′后，验证e（kθ′，P）＝e（H1（m），yH0（mw，Ui））是否成立。若成立，用户U计算θ＝kθ′，把代理签名去盲后，得到对消息m的代理盲签名（mw，m，θ，Ui）。至此，代理盲签名步骤已完毕。

任意验证者可对消息m的代理盲签名（mw，m，θ，Ui）进行有效性验证，e（θ，P）＝e（H1（m），yH0（mw，Ui）），若成立，则签名有效。

2.2.3 正确性分析

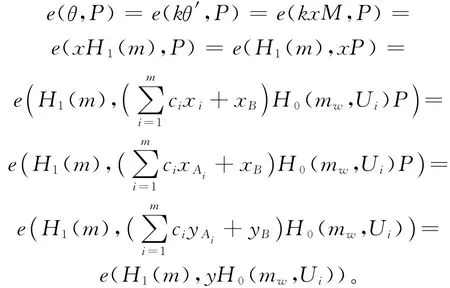
2.3 安全性分析

2.3.1 不可伪造性

2.3.2 可验证性

在有效的代理盲多重签名（mw，m，θ，Ui）中含有代理授权书mw，代理授权书涵盖了原始签名人Ai与代理签名人B的身份、代理签名文件的范围和代理授权终止的时间、代理权限范围等确切信息，因此任何人都能够区分原始签名人Ai与代理签名人B的签名。本代理盲多重签名方案满足了代理盲签名的可验证性、可区分性、可识别性、不可否认性和防止滥用性。

2.3.3 盲性

用户U通过哈希函数H1（m）盲因子k对消息m进行了盲化，化成H1（m），并进一步转化成M，代理签名人B在整个代理签名过程中根本无法看到m，也无法根据接收到的M求解出m，哈希函数H1（m）不可解，盲因子k也未知，因此消息m对代理签名人B来说是盲性的。

2.3.4 不可链接性

鉴于双线性对DLP问题的难解性，在θ＝kθ′中，已知θ与θ′，无法求解k。即使代理签名人B在公布的签名（mw，m，θ，Ui）中获取θ后保存了θ′、M，但仍无法通过θ＝kθ′计算出盲因子k。由此，代理签名人B无法确定（mw，m，θ，Ui）是他的第几次签名，所以本方案是满足不可链接性的。

2.4 效率分析

本方案中只用了双线性对2次，全部用于验证等式是否成立。另外，原始签名人Ai、代理签名人B、用户U三方之间，彼此通信次数很少，并且信息通信量也很小，该设计提高了运行效率。与文献［9］的方案相比，不用进行Zq中的求逆运算，而且基于双线性对可以提高方案的安全性。

3 结束语

本文先对一个基于椭圆曲线的盲多重代理签名进行安全性分析，发现其存在可伪造性，进一步基于双线性对提出了改进的盲多重代理签名方案，并进行了较为详细的安全性分析，该方案不但能抵抗强伪造攻击，而且具有不可追踪性、可验证性。对方案的效率性分析表明，与文献［9］的方案相比，本方案具有更高的效率。由于双线性对运算较复杂，利用较少的双线性对运算，设计出更加安全、效率更高的方案是进一步研究的重点。

［1］ Chaum D.Blind signatures for untraceble payments［M］.New York：Plenum Press，1983：199－203.

［2］ Mambo M，Usuda K，Okamoto E.Proxy signature：delegation of the power to sign messages［J］.IEICE Trans on Fundamentals of Electronics Communications and Computer Sciences，1996，E79－A（9）：1338－1354.

［3］ Mambo M，Usuda K，Okamoto E.Proxy signature for delegating signing operation［C］／／Proc of the 3rd ACM Conference on Computer and Communications Security.New Delhi，India：ACM Press，1996：48－57.

［4］ Yi Lijiang，Bai Guoqiang，Xiao Guozhen.Proxy multi－signature schemes［J］.Electronic Letters，2000，36 （6）：527－528.

［5］ 左为平，王彩芬，樊 睿，等.一种基于身份的代理多重签名方案［J］.西北师范大学学报：自然科学版，2007，43（4）：33－36.

［6］ 贺 军，李丽娟，李喜梅，等.前向安全的代理多重签名方案［J］.计算机工程，2010，36（1）：422－426.

［7］ 孟纯煜，殷新春，宋春来.基于身份的盲签名在电子现金中的应用［J］.合肥工业大学学报：自然科学版，2007，30（10）：1265－1266，1270.

［8］ 彭丽慧，张建中.基于双线性对的代理签名方案［J］.计算机工程，2010，36（24）：132－141.

［9］ 祁 明，Harn L.基于离散对数的若干新型代理签名方案［J］.电子学报，2000，28（11）：111－115.

［10］ 王 璐，亢保元.对两个代理盲多重签名的分析和改进［J］.计算机与数学工程，2012，40（10）：102－104.

［11］ Padro C，Saez G.Detection of cheaters in vector space secret sharing schemes［J］.Journal of Designs，Codes and Cryptography，1999，16（1）：75－85.

［12］ 纪家慧，李大兴.来自双线性配对的新的代理多签名、多代理签名和多代理多签名体制［J］.计算机学报，2004，27（10）：1429－1435.

［13］ Rong Xinglu，Zheng Fucao，Yuan zhou.Proxy blind multisignature scheme without a secure channel［J］.Applied Mathematics and Computation，2005，164（1）：179－187.

［14］ Boneh D，Lynn B，Shacham H.Short signatures from the weil pairing［C］／／Proc of ASIACRYPT'01.Berlin：Springer－Verlag，2001：514－532.