实用的MEMS惯性器件外场标定方法*

任建新，杜亚宁，杨星辉，赵兴梅

（西北工业大学自动化学院，陕西西安 710072）

0 引言

MEMS惯性器件在成本、体积、可靠性等方面具有显著优势，但是其发展却受到精度的制约［1］，由于输出中总是包含着各种误差项，因此，有必要对它的主要误差系数进行标定。然而，与传统的高精度惯性传感器相比，低精度的MEMS惯性器件有其特殊性，主要表现在零偏重复性和稳定性较差［2］;其次，在实际的工程应用中，很少有条件提供高精度的实验室标定设备［3］，因此，设计一种针对MEMS惯性器件的简易可行的外场标定方法非常有必要。

本文从分析基于ADIS16405型号的MEMS惯性测量单元的误差模型出发［4］，结合基于椭球模值约束的外场标定算法，分别设计了针对MEMS加速度计和MEMS陀螺仪的实验编排方案，最后对比实际外场标定与实验室标定结果，证明了该标定方法的可行性。

1 MEMS惯性器件的误差分析

与传统的惯性传感器类似，可将MEMS 惯性器件的误差主要分为零位误差、刻度系数误差和非正交误差。

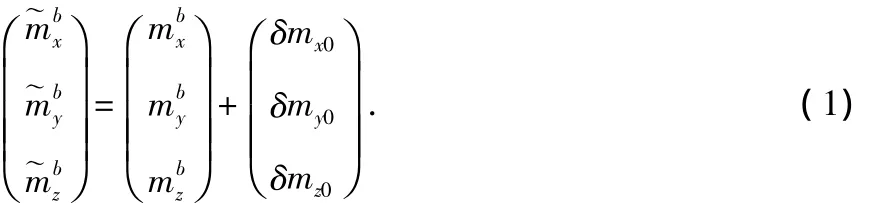
其中，δmx0，δmy0，δmz0为 MEMS 三轴传感器的零位误差。

2）刻度系数误差Km是由于三轴传感器的灵敏度实际输出与出厂说明书上不同而引起的误差，则刻度系数误差为

3）非正交误差Tm是由于制造时不能保证三轴传感器测的3个测量轴正交而引起的误差，当MEMS三轴传感器的敏感轴不处于正交时，则会引起非正交误差

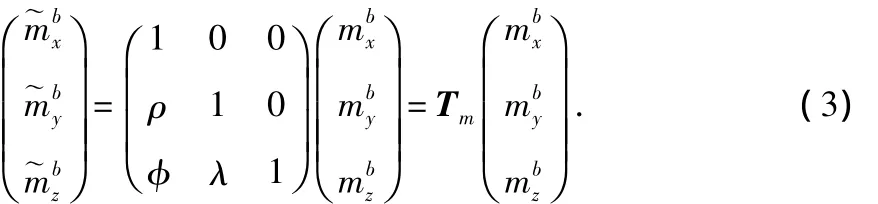
综上所述，MEMS三轴传感器的误差模型可以表述为

2 外场标定的原理与算法

在静态情况下，MEMS加速度计的输出为当地的重力矢量g，虽然g在空间系的投影未知，但是满足:

‖g‖2=g，其中，‖g‖2为矢量g的2范数。那么g即为当地重力矢量的模值，它为MEMS加速度计外场标定提供模值约束;MEMS陀螺仪的输出为地球自转角速度ωie，然而由于地球自转角速度太小，基本淹没在MEMS陀螺仪的噪声中，无法利用其实现对误差模型参数的辨识，因此，必须对其施加额外的角运动来完成外场标定，但是，在没有精密速率转台的情况下，施加准确的角速率是不现实的［5］，因此，利用角位置来实现角度模值约束。

2.1 MEMS加速度计外场标定算法

假设在理想状态下不存在传感器的各项误差，那么传感器输出矢量的模值应该等于约束模值，由式（4）得出

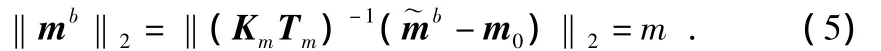
其中，m为约束模值。

对式（5）两边进行平方得出

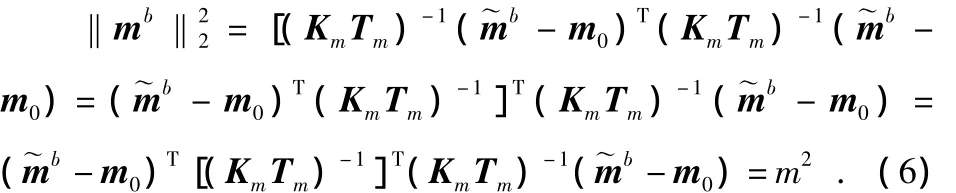
由于 mb=为传感器的测量真值，则

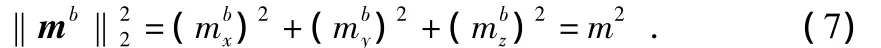
从式（7）中可以看出，从解析几何的数学意义角度考虑，理想状态下三轴传感器的输出在三轴坐标系里是以（0，0，0）为圆心，模值约束值m为半径的标准圆球。然而由于各种误差的存在，使得球体在坐标系中的形状和位置发生变化。

1）当MEMS传感器存在零位误差时

由式（8）可以得出，在解析几何意义上，圆球的圆心偏离的原点（0，0，0）变为（δmx0，δmy0，δmz0）。

2）当MEMS传感器存在刻度系数误差时

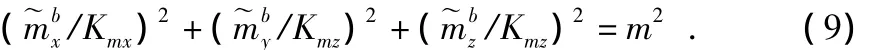
由式（9）可以得出，传感器的输出在解析几何意义上变成一个椭球。

3）当传感器存在非正交误差时

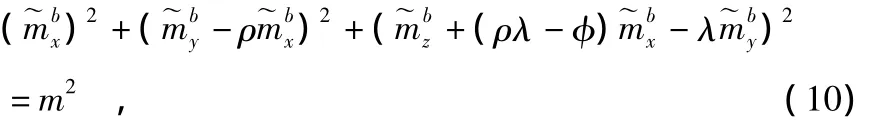
令式（10）与一般椭球方程相比较，可以得出传感器的输出在解析几何意义上已经不是一个严格意义的椭圆，而是一个关于原点对称的扁球体。

根据式（4）得出

将式（11）矩阵形式展开分别得出

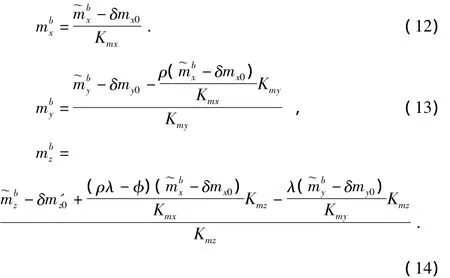
将式（12）、式（13）、式（14）分别代入式（7）构建出包含着零位误差系数（δmx0，δmy0，δmz0），刻度系数误差（Kmx，Kmy，Kmz），以及非正交误差系数（ρ，φ，λ），外场标定的过程就是通过采集n（n＞9）组测量数据，通过总体最小二乘法来确定上述9个未知参数，该算法即为椭球模值约束算法［6，7］。

2.2 MEMS陀螺仪外场标定算法

前面提到MEMS陀螺仪标定需要利用角度模值约束，因此，有必要借助辅助设备和MEMS测量单元的自身安装壳体，通过转动特殊的角度即角速率陀螺的积分值来实现外场标定。在此分2个步骤进行标定:首先，标定刻度系数误差和非正交误差，采用顺时针和逆时针的旋转抵消地球自转和陀螺零偏;然后，利用已获得的刻度系数误差和非正交误差来标定零偏误差。

对于第一步的标定，给定一个光滑平面和一个基准平面，绕某一敏感轴手动旋转MEMS壳体，根据上述式（4）误差模型得出

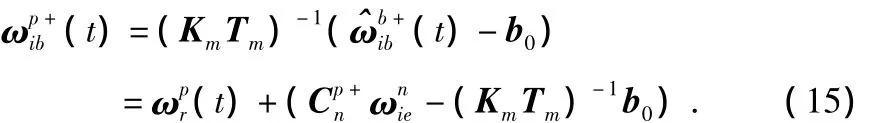
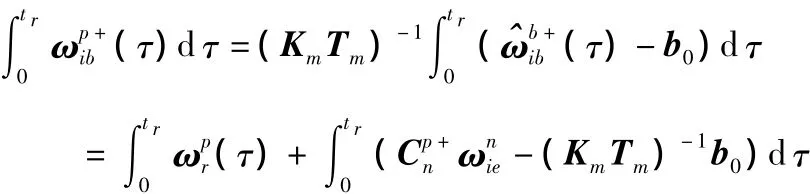
同理，沿着同一个轴逆时针旋转并积分时，可得出

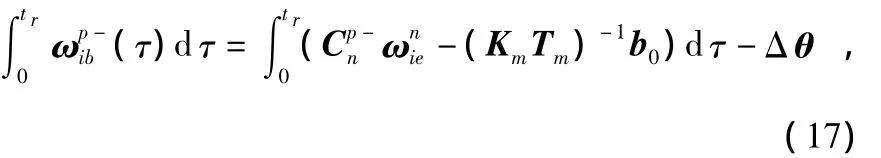
式中 Δ θ为转动的已知角度，即以此来提供模值约束。将两式相减并将等式两端同时去模值得出

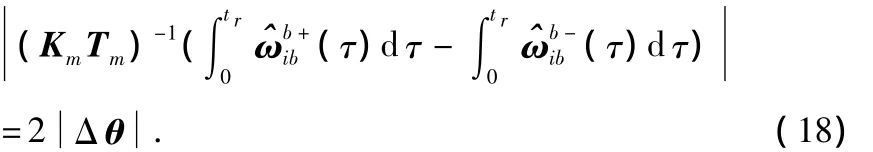
将两边同时平方并展开矩阵式得出

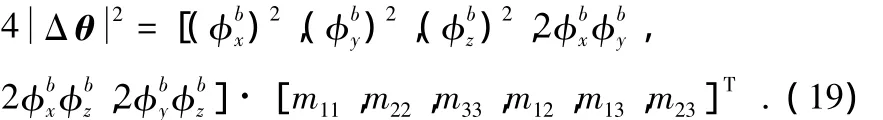
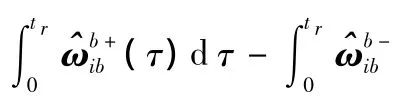
将式（20）转换为椭球形式，从而实现利用椭球模值约束法来标定MEMS陀螺仪。

第二步，标定陀螺仪的零偏，对于静态情况下的MEMS陀螺仪，由式（4）得出

则进一步得出

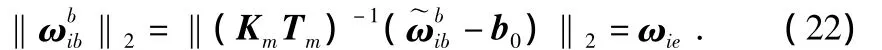
两边同时平方得出

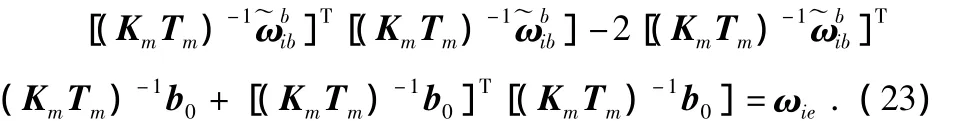
假设在不同的静态位置，获得MEMS陀螺仪输出为

在求得刻度系数误差和非正交误差的基础上，并且获得足够多的静态位置数据，即可利用总体最小二乘［8］或一般最小二乘［9］来计算零偏误差。

3 外场标定的过程

1）对于MEMS加速度计来说，当地的重力加速度的模值比较大，因此，完全可以作为加速度计外场标定时的模值约束。为了更加有效地获得采集数据，在几何意义上使数据尽可能多地分布在椭球面上，就需要使MEMS惯性器件绕3个敏感轴分别旋转不同的角度，数据采集过程中必须保持器件固定良好，3个敏感轴分别采集多组数据。

2）对于MEMS陀螺仪来说，选定2个相互垂直的光滑平面，在此选取了实验室地面和与水平面垂直的方凳侧面，将六面体安装壳体放在水平面紧靠方凳侧面，并且在方凳上标记其初始位置，然后绕着垂直水平面的旋转轴轻轻转动壳体360°（旋转的过程尽量保持在水平面上），当壳体与标记初始位置重合即说明旋转了1周，然后再逆时针旋转360°，忽略各项误差，顺时针减去逆时针之差为720°。然后再进行先逆时针旋转，后顺时针旋转，则前后之差为-720°，以此类推3个正交面共可获得6组数据。然后再将MEMS器件在壳体中变换不同的角度，再进行上述测量，以获得更多的数据。

3）在实验室条件下，采用位置转台对MEMS加速度计进行1gn范围内的标定;采用速率转台设定多组不同的速率值对MEMS陀螺仪进行标定，最终得出实验室标定结果与外场标定结果的比较如表1和表2所示。

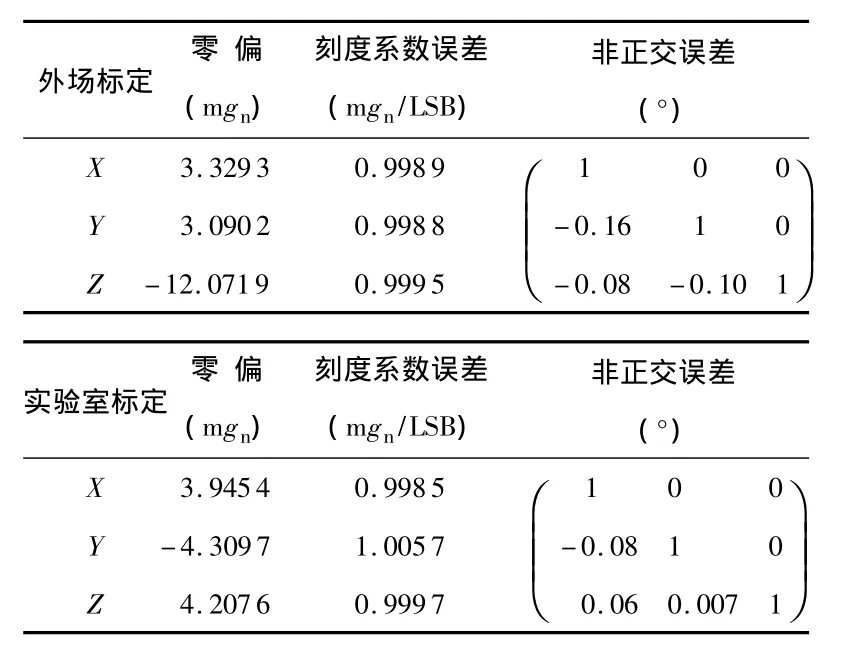
表1 MEMS加速度计标定结果Tab 1 Result of calibration for MEMS accelerometer

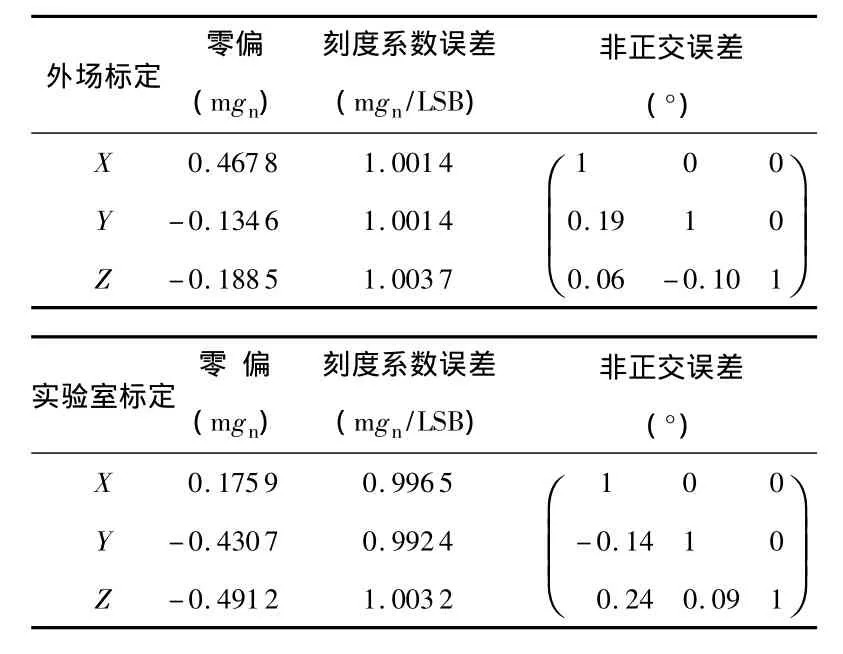
表2 MEMS陀螺仪标定结果Tab 2 Result of calibration for MEMS gyroscope

通过对表1和表2的实验室标定和外场标定结果对比可以得出，两者的整体吻合程度较高，其中加速度计零偏外场标定精度优于10 mgn（标称范围为±50 mgn），陀螺的零偏外场标定精度优于0.5°/s（标称范围为±3°/s），两者的刻度系数误差的外场标定一致度达到98%以上，基本满足了工程应用条件下MEMS惯性器件的外场标定要求。

4 结论

本文所提方法有效地实现了MEMS惯性器件在不具备实验室条件（转台、分度头等）下的外场标定，实验步骤简易可行，对主要的误差参数实现了较高精度的标定，提高了MEMS惯性器件的标定效率，具有较高的工程实用性和可靠性。

［1］梅春波.基于MEMS惯性器件应急地平仪研究［D］.西安:西北工业大学，2011.

［2］Shen S C，Chen C J，Huang H J.A new calibration method for MEMS inertial sensor module［C］//2010 IEEE 11th IEEE International Workshop on Advanced Motion Control，2010:106-111.

［3］Sye Z F，Aggarwal P，Goodall C，et al.A new multi-position calibration method for MEMS inertial navigation systems［J］.Measurement Science and Technology，2007，18:1897-1907.

［4］陈宝毅.MEMS惯性器件的数据采集与误差分析技术研究［D］.哈尔滨:哈尔滨工程大学，2009.

［5］Zhang Hongliang，Wu Yuanxin，Wu Wenqi，et al.Improved multipositon calibration for inertial measurement units［J］.Measurement Science and Technology，2010，21:1-11.

［6］Gebre-Egziabher D，Elkaim G H，Powell J D，et al.Calibration of strapdown magnetometers in the magnetic field domain［J］.ASCE Journal of Aerospace Engineering，2006，19（2）:1-16.

［7］Gebre-Egziabher D，Elkaim G H，Powell J D，et al.A non-linear，two-step estimation algorithm for calibration solid-state strapdown magnetometers［C］//8th International Conference on Navigation Systems，St.Peterburg，2011:28-30.

［8］鲁铁定.基于整体最小二乘法的线性回归建模和解法［J］.武汉大学学报:信息科学版，2008，33（5）:504-507.

［9］鲁铁定.总体最小二乘的迭代算法［J］.武汉大学学报:信息科学版，2010，35（11）:1352-1355.